Rediscovering Argumentation Principles Utilizing Collective Attacks

Argumentation Frameworks (AFs) are a key formalism in AI research. Their semantics have been investigated in terms of principles, which define characteristic properties in order to deliver guidance for analysing established and developing new semantics. Because of the simple structure of AFs, many desired properties hold almost trivially, at the same time hiding interesting concepts behind syntactic notions. We extend the principle-based approach to Argumentation Frameworks with Collective Attacks (SETAFs) and provide a comprehensive overview of common principles for their semantics. Our analysis shows that investigating principles based on decomposing the given SETAF (e.g. directionality or SCC-recursiveness) poses additional challenges in comparison to usual AFs. We introduce the notion of the reduct as well as the modularization principle for SETAFs which will prove beneficial for this kind of investigation. We then demonstrate how our findings can be utilized for incremental computation of extensions and give a novel parameterized tractability result for verifying preferred extensions.

Aspartix-V21

In this solver description we present ASPARTIX-V, in its 2021 edition, which participates in the International Competition on Computational Models of Argumentation (ICCMA) 2021. ASPARTIX-V is capable of solving all classical (static) reasoning tasks part of ICCMA'21 and extends the ASPARTIX system suite by incorporation of recent ASP language constructs (e.g. conditional literals), domain heuristics within ASP, and multi-shot methods. In this light ASPARTIX-V deviates from the traditional focus of ASPARTIX on monolithic approaches (i.e., one-shot solving via a single ASP encoding) to further enhance performance.

Expressiveness of SETAFs and Support-Free ADFs under 3-valued Semantics

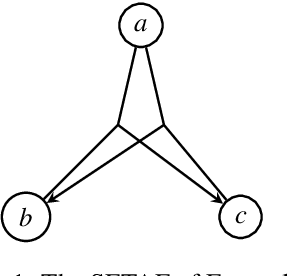
Generalizing the attack structure in argumentation frameworks (AFs) has been studied in different ways. Most prominently, the binary attack relation of Dung frameworks has been extended to the notion of collective attacks. The resulting formalism is often termed SETAFs. Another approach is provided via abstract dialectical frameworks (ADFs), where acceptance conditions specify the relation between arguments; restricting these conditions naturally allows for so-called support-free ADFs. The aim of the paper is to shed light on the relation between these two different approaches. To this end, we investigate and compare the expressiveness of SETAFs and support-free ADFs under the lens of 3-valued semantics. Our results show that it is only the presence of unsatisfiable acceptance conditions in support-free ADFs that discriminate the two approaches.

Algorithms and Conditional Lower Bounds for Planning Problems

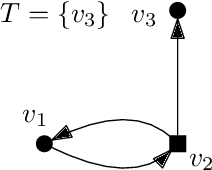
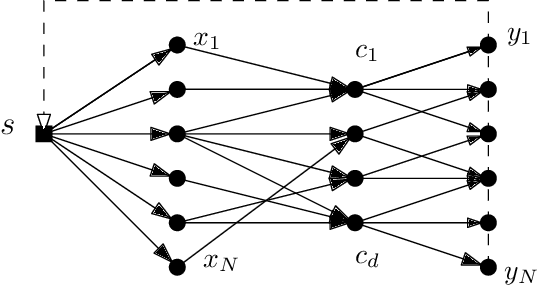
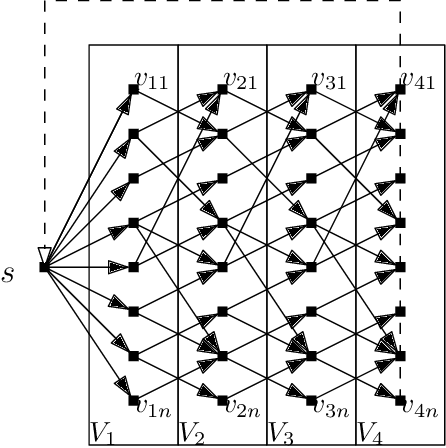
We consider planning problems for graphs, Markov decision processes (MDPs), and games on graphs. While graphs represent the most basic planning model, MDPs represent interaction with nature and games on graphs represent interaction with an adversarial environment. We consider two planning problems where there are k different target sets, and the problems are as follows: (a) the coverage problem asks whether there is a plan for each individual target set, and (b) the sequential target reachability problem asks whether the targets can be reached in sequence. For the coverage problem, we present a linear-time algorithm for graphs and quadratic conditional lower bound for MDPs and games on graphs. For the sequential target problem, we present a linear-time algorithm for graphs, a sub-quadratic algorithm for MDPs, and a quadratic conditional lower bound for games on graphs. Our results with conditional lower bounds establish (i) model-separation results showing that for the coverage problem MDPs and games on graphs are harder than graphs and for the sequential reachability problem games on graphs are harder than MDPs and graphs; (ii) objective-separation results showing that for MDPs the coverage problem is harder than the sequential target problem.

Technical Note: Exploring Σ^P_2 / Π^P_2-hardness for Argumentation Problems with fixed distance to tractable classes

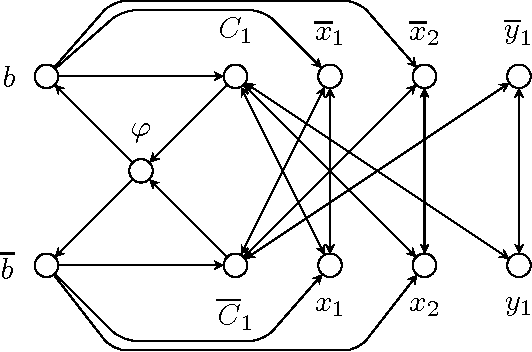
We study the complexity of reasoning in abstracts argumentation frameworks close to graph classes that allow for efficient reasoning methods, i.e.\ to one of the classes of acyclic, noeven, biparite and symmetric AFs. In this work we show that certain reasoning problems on the second level of the polynomial hierarchy still maintain their full complexity when restricted to instances of fixed distance to one of the above graph classes.

Making Use of Advances in Answer-Set Programming for Abstract Argumentation Systems

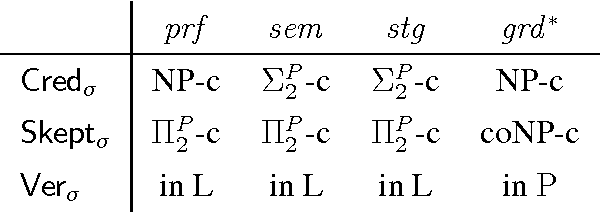
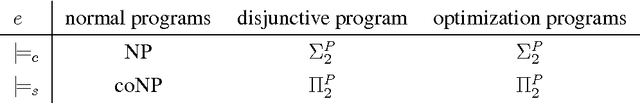
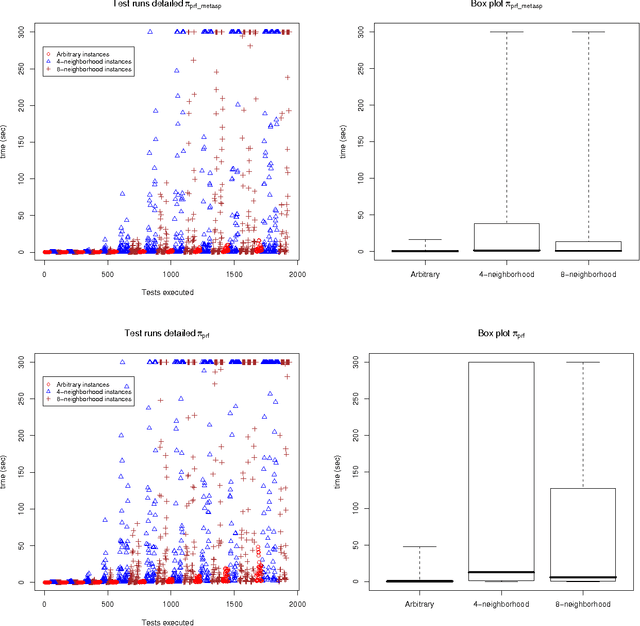
Dung's famous abstract argumentation frameworks represent the core formalism for many problems and applications in the field of argumentation which significantly evolved within the last decade. Recent work in the field has thus focused on implementations for these frameworks, whereby one of the main approaches is to use Answer-Set Programming (ASP). While some of the argumentation semantics can be nicely expressed within the ASP language, others required rather cumbersome encoding techniques. Recent advances in ASP systems, in particular, the metasp optimization frontend for the ASP-package gringo/claspD provides direct commands to filter answer sets satisfying certain subset-minimality (or -maximality) constraints. This allows for much simpler encodings compared to the ones in standard ASP language. In this paper, we experimentally compare the original encodings (for the argumentation semantics based on preferred, semi-stable, and respectively, stage extensions) with new metasp encodings. Moreover, we provide novel encodings for the recently introduced resolution-based grounded semantics. Our experimental results indicate that the metasp approach works well in those cases where the complexity of the encoded problem is adequately mirrored within the metasp approach.

dynPARTIX - A Dynamic Programming Reasoner for Abstract Argumentation

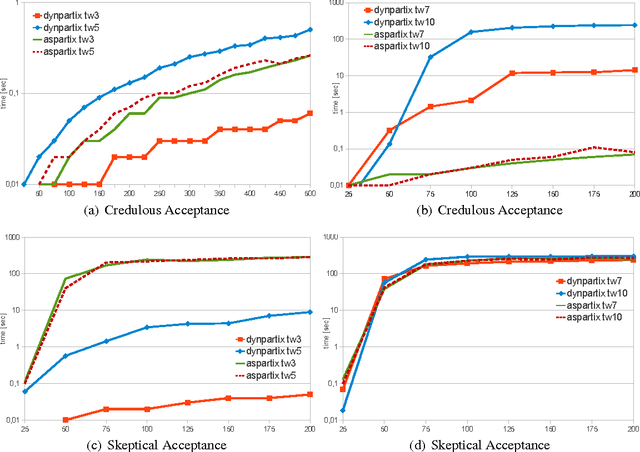
The aim of this paper is to announce the release of a novel system for abstract argumentation which is based on decomposition and dynamic programming. We provide first experimental evaluations to show the feasibility of this approach.