Technical Note: Exploring Σ^P_2 / Π^P_2-hardness for Argumentation Problems with fixed distance to tractable classes

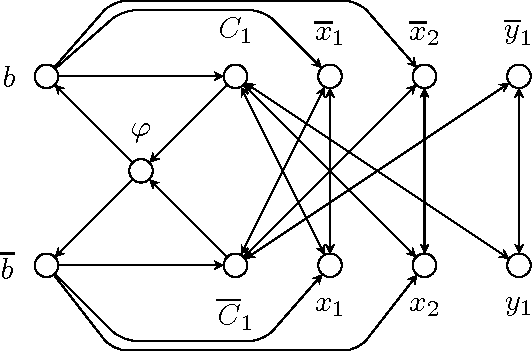
We study the complexity of reasoning in abstracts argumentation frameworks close to graph classes that allow for efficient reasoning methods, i.e.\ to one of the classes of acyclic, noeven, biparite and symmetric AFs. In this work we show that certain reasoning problems on the second level of the polynomial hierarchy still maintain their full complexity when restricted to instances of fixed distance to one of the above graph classes.