An epistemic logic for modeling decisions in the context of incomplete knowledge

Substantial efforts have been made in developing various Decision Modeling formalisms, both from industry and academia. A challenging problem is that of expressing decision knowledge in the context of incomplete knowledge. In such contexts, decisions depend on what is known or not known. We argue that none of the existing formalisms for modeling decisions are capable of correctly capturing the epistemic nature of such decisions, inevitably causing issues in situations of uncertainty. This paper presents a new language for modeling decisions with incomplete knowledge. It combines three principles: stratification, autoepistemic logic, and definitions. A knowledge base in this language is a hierarchy of epistemic theories, where each component theory may epistemically reason on the knowledge in lower theories, and decisions are made using definitions with epistemic conditions.

Using Symmetries to Lift Satisfiability Checking

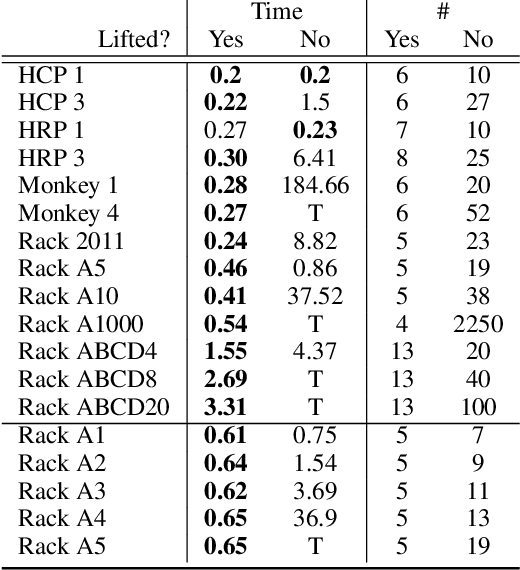
We analyze how symmetries can be used to compress structures (also known as interpretations) onto a smaller domain without loss of information. This analysis suggests the possibility to solve satisfiability problems in the compressed domain for better performance. Thus, we propose a 2-step novel method: (i) the sentence to be satisfied is automatically translated into an equisatisfiable sentence over a ``lifted'' vocabulary that allows domain compression; (ii) satisfiability of the lifted sentence is checked by growing the (initially unknown) compressed domain until a satisfying structure is found. The key issue is to ensure that this satisfying structure can always be expanded into an uncompressed structure that satisfies the original sentence to be satisfied. We present an adequate translation for sentences in typed first-order logic extended with aggregates. Our experimental evaluation shows large speedups for generative configuration problems. The method also has applications in the verification of software operating on complex data structures. Further refinements of the translation are left for future work.

On Nested Justification Systems (full version)

Justification theory is a general framework for the definition of semantics of rule-based languages that has a high explanatory potential. Nested justification systems, first introduced by Denecker et al. (2015), allow for the composition of justification systems. This notion of nesting thus enables the modular definition of semantics of rule-based languages, and increases the representational capacities of justification theory. As we show in this paper, the original semantics for nested justification systems lead to the loss of information relevant for explanations. In view of this problem, we provide an alternative characterization of semantics of nested justification systems and show that this characterization is equivalent to the original semantics. Furthermore, we show how nested justification systems allow representing fixpoint definitions (Hou and Denecker 2009).

Quantification and aggregation over concepts of the ontology

The first phase of developing an intelligent system is the selection of an ontology of symbols representing relevant concepts of the application domain. These symbols are then used to represent the knowledge of the domain. This representation should be \emph{elaboration tolerant}, in the sense that it should be convenient to modify it to take into account new knowledge or requirements. Unfortunately, current formalisms require a significant rewrite of that representation when the new knowledge is about the \emph{concepts} themselves: the developer needs to "\emph{reify}" them. This happens, for example, when the new knowledge is about the number of concepts that satisfy some conditions. The value of expressing knowledge about concepts, or "intensions", has been well-established in \emph{modal logic}. However, the formalism of modal logic cannot represent the quantifications and aggregates over concepts that some applications need. To address this problem, we developed an extension of first order logic that allows referring to the \emph{intension} of a symbol, i.e., to the concept it represents. We implemented this extension in IDP-Z3, a reasoning engine for FO($\cdot$) (aka FO-dot), a logic-based knowledge representation language. This extension makes the formalism more elaboration tolerant, but also introduces the possibility of syntactically incorrect formula. Hence, we developed a guarding mechanism to make formula syntactically correct, and a method to verify correctness. The complexity of this method is linear with the length of the formula. This paper describes these extensions, how their relate to intensions in modal logic and other formalisms, and how they allowed representing the knowledge of four different problem domains in an elaboration tolerant way.

IDP-Z3: a reasoning engine for FO

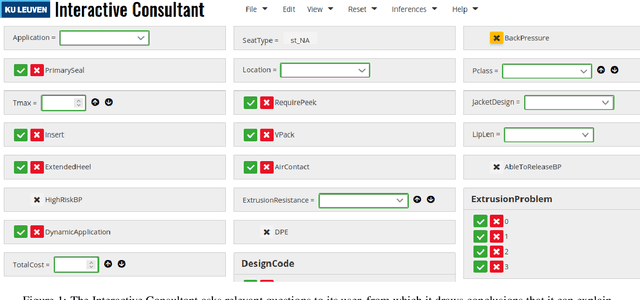
An important sign of intelligence is the capacity to apply a body of knowledge to a particular situation in order to not only derive new knowledge, but also to determine relevant questions or provide explanations. Developing interactive systems capable of performing such a variety of reasoning tasks for the benefits of its users has proved difficult, notably for performance and/or development cost reasons. Still, recently, a reasoning engine, called IDP3, has been used to build such systems, but it lacked support for arithmetic operations, seriously limiting its usefulness. We have developed a new reasoning engine, IDP-Z3, that removes this limitation, and we put it to the test in four knowledge-intensive industrial use cases. This paper describes FO(.) (aka FO-dot), the language used to represent knowledge in the IDP3 and IDP-Z3 system. It then describes the generic reasoning tasks that IDP-Z3 can perform, and how we used them to build a generic user interface, called the Interactive Consultant. Finally, it reports on the four use cases. In these four use cases, the interactive applications based on IDP-Z3 were capable of intelligent behavior of value to users, while having a low development cost (typically 10 days) and an acceptable response time (typically below 3 seconds). Performance could be further improved, in particular for problems on larger domains.

Analyzing Semantics of Aggregate Answer Set Programming Using Approximation Fixpoint Theory

Aggregates provide a concise way to express complex knowledge. While they are easily understood by humans, formalizing aggregates for answer set programming (ASP) has proven to be challenging . The literature offers many approaches that are not always compatible. One of these approaches, based on Approximation Fixpoint Theory (AFT), has been developed in a logic programming context and has not found much resonance in the ASP-community. In this paper we revisit this work. We introduce the abstract notion of a ternary satisfaction relation and define stable semantics in terms of it. We show that ternary satisfaction relations bridge the gap between the standard Gelfond-Lifschitz reduct, and stable semantics as defined in the framework of AFT. We analyse the properties of ternary satisfaction relations for handling aggregates in ASP programs. Finally, we show how different methods for handling aggregates taken from the literature can be described in the framework and we study the corresponding ternary satisfaction relations.

Exploiting Game Theory for Analysing Justifications

Justification theory is a unifying semantic framework. While it has its roots in non-monotonic logics, it can be applied to various areas in computer science, especially in explainable reasoning; its most central concept is a justification: an explanation why a property holds (or does not hold) in a model. In this paper, we continue the study of justification theory by means of three major contributions. The first is studying the relation between justification theory and game theory. We show that justification frameworks can be seen as a special type of games. The established connection provides the theoretical foundations for our next two contributions. The second contribution is studying under which condition two different dialects of justification theory (graphs as explanations vs trees as explanations) coincide. The third contribution is establishing a precise criterion of when a semantics induced by justification theory yields consistent results. In the past proving that such semantics were consistent took cumbersome and elaborate proofs. We show that these criteria are indeed satisfied for all common semantics of logic programming. This paper is under consideration for acceptance in Theory and Practice of Logic Programming (TPLP).

The informal semantics of Answer Set Programming: A Tarskian perspective

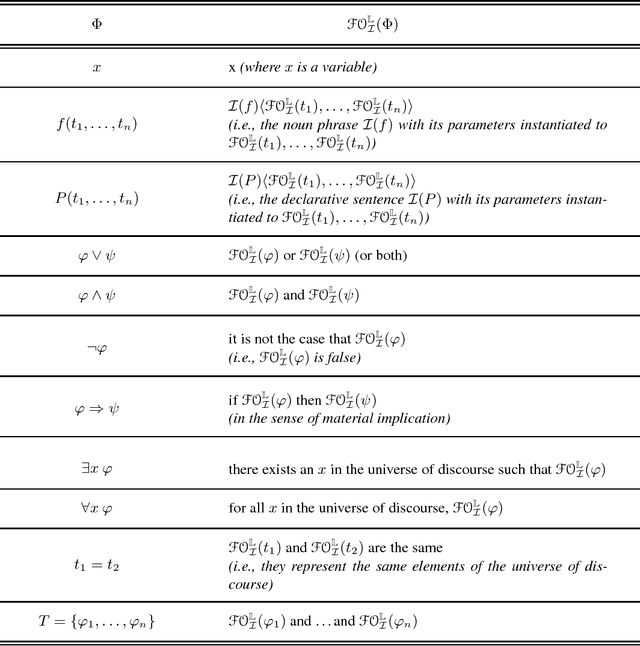
In Knowledge Representation, it is crucial that knowledge engineers have a good understanding of the formal expressions that they write. What formal expressions state intuitively about the domain of discourse is studied in the theory of the informal semantics of a logic. In this paper we study the informal semantics of Answer Set Programming. The roots of answer set programming lie in the language of Extended Logic Programming, which was introduced initially as an epistemic logic for default and autoepistemic reasoning. In 1999, the seminal papers on answer set programming proposed to use this logic for a different purpose, namely, to model and solve search problems. Currently, the language is used primarily in this new role. However, the original epistemic intuitions lose their explanatory relevance in this new context. How answer set programs are connected to the specifications of problems they model is more easily explained in a classical Tarskian semantics, in which models correspond to possible worlds, rather than to belief states of an epistemic agent. In this paper, we develop a new theory of the informal semantics of answer set programming, which is formulated in the Tarskian setting and based on Frege's compositionality principle. It differs substantially from the earlier epistemic theory of informal semantics, providing a different view on the meaning of the connectives in answer set programming and on its relation to other logics, in particular classical logic.

Implementing a Relevance Tracker Module

PC(ID) extends propositional logic with inductive definitions: rule sets under the well-founded semantics. Recently, a notion of relevance was introduced for this language. This notion determines the set of undecided literals that can still influence the satisfiability of a PC(ID) formula in a given partial assignment. The idea is that the PC(ID) solver can make decisions only on relevant literals without losing soundness and thus safely ignore irrelevant literals. One important insight that the relevance of a literal is completely determined by the current solver state. During search, the solver state changes have an effect on the relevance of literals. In this paper, we discuss an incremental, lightweight implementation of a relevance tracker module that can be added to and interact with an out-of-the-box SAT(ID) solver.

The KB paradigm and its application to interactive configuration

The knowledge base paradigm aims to express domain knowledge in a rich formal language, and to use this domain knowledge as a knowledge base to solve various problems and tasks that arise in the domain by applying multiple forms of inference. As such, the paradigm applies a strict separation of concerns between information and problem solving. In this paper, we analyze the principles and feasibility of the knowledge base paradigm in the context of an important class of applications: interactive configuration problems. In interactive configuration problems, a configuration of interrelated objects under constraints is searched, where the system assists the user in reaching an intended configuration. It is widely recognized in industry that good software solutions for these problems are very difficult to develop. We investigate such problems from the perspective of the KB paradigm. We show that multiple functionalities in this domain can be achieved by applying different forms of logical inferences on a formal specification of the configuration domain. We report on a proof of concept of this approach in a real-life application with a banking company. To appear in Theory and Practice of Logic Programming (TPLP).