The informal semantics of Answer Set Programming: A Tarskian perspective
Paper and Code
Jan 26, 2019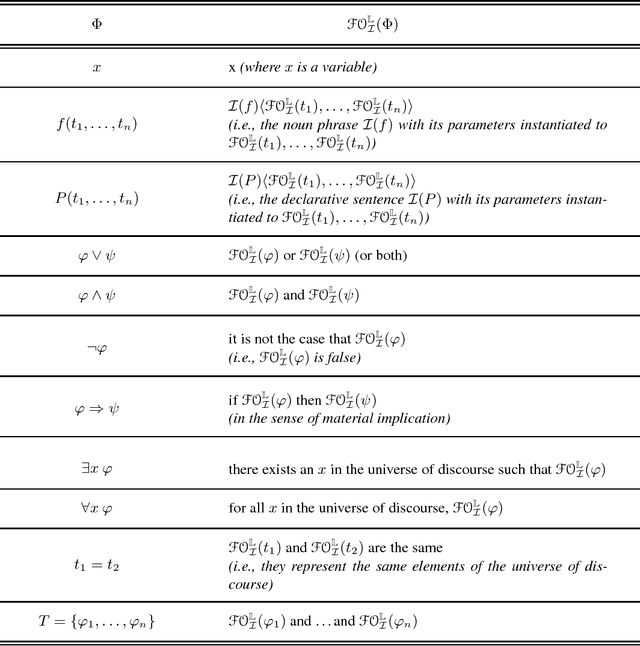



In Knowledge Representation, it is crucial that knowledge engineers have a good understanding of the formal expressions that they write. What formal expressions state intuitively about the domain of discourse is studied in the theory of the informal semantics of a logic. In this paper we study the informal semantics of Answer Set Programming. The roots of answer set programming lie in the language of Extended Logic Programming, which was introduced initially as an epistemic logic for default and autoepistemic reasoning. In 1999, the seminal papers on answer set programming proposed to use this logic for a different purpose, namely, to model and solve search problems. Currently, the language is used primarily in this new role. However, the original epistemic intuitions lose their explanatory relevance in this new context. How answer set programs are connected to the specifications of problems they model is more easily explained in a classical Tarskian semantics, in which models correspond to possible worlds, rather than to belief states of an epistemic agent. In this paper, we develop a new theory of the informal semantics of answer set programming, which is formulated in the Tarskian setting and based on Frege's compositionality principle. It differs substantially from the earlier epistemic theory of informal semantics, providing a different view on the meaning of the connectives in answer set programming and on its relation to other logics, in particular classical logic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge