Frank Wolter
Current and Future Challenges in Knowledge Representation and Reasoning
Aug 08, 2023Abstract:Knowledge Representation and Reasoning is a central, longstanding, and active area of Artificial Intelligence. Over the years it has evolved significantly; more recently it has been challenged and complemented by research in areas such as machine learning and reasoning under uncertainty. In July 2022 a Dagstuhl Perspectives workshop was held on Knowledge Representation and Reasoning. The goal of the workshop was to describe the state of the art in the field, including its relation with other areas, its shortcomings and strengths, together with recommendations for future progress. We developed this manifesto based on the presentations, panels, working groups, and discussions that took place at the Dagstuhl Workshop. It is a declaration of our views on Knowledge Representation: its origins, goals, milestones, and current foci; its relation to other disciplines, especially to Artificial Intelligence; and on its challenges, along with key priorities for the next decade.
Temporalising Unique Characterisability and Learnability of Ontology-Mediated Queries
Jun 13, 2023Abstract:Recently, the study of the unique characterisability and learnability of database queries by means of examples has been extended to ontology-mediated queries. Here, we study in how far the obtained results can be lifted to temporalised ontology-mediated queries. We provide a systematic introduction to the relevant approaches in the non-temporal case and then show general transfer results pinpointing under which conditions existing results can be lifted to temporalised queries.
Reverse Engineering of Temporal Queries Mediated by LTL Ontologies
May 04, 2023

Abstract:In reverse engineering of database queries, we aim to construct a query from a given set of answers and non-answers; it can then be used to explore the data further or as an explanation of the answers and non-answers. We investigate this query-by-example problem for queries formulated in positive fragments of linear temporal logic LTL over timestamped data, focusing on the design of suitable query languages and the combined and data complexity of deciding whether there exists a query in the given language that separates the given answers from non-answers. We consider both plain LTL queries and those mediated by LTL-ontologies.
How to Approximate Ontology-Mediated Queries
Jul 12, 2021

Abstract:We introduce and study several notions of approximation for ontology-mediated queries based on the description logics ALC and ALCI. Our approximations are of two kinds: we may (1) replace the ontology with one formulated in a tractable ontology language such as ELI or certain TGDs and (2) replace the database with one from a tractable class such as the class of databases whose treewidth is bounded by a constant. We determine the computational complexity and the relative completeness of the resulting approximations. (Almost) all of them reduce the data complexity from coNP-complete to PTime, in some cases even to fixed-parameter tractable and to linear time. While approximations of kind (1) also reduce the combined complexity, this tends to not be the case for approximations of kind (2). In some cases, the combined complexity even increases.
First Order-Rewritability and Containment of Conjunctive Queries in Horn Description Logics
Nov 19, 2020Abstract:We study FO-rewritability of conjunctive queries in the presence of ontologies formulated in a description logic between EL and Horn-SHIF, along with related query containment problems. Apart from providing characterizations, we establish complexity results ranging from ExpTime via NExpTime to 2ExpTime, pointing out several interesting effects. In particular, FO-rewriting is more complex for conjunctive queries than for atomic queries when inverse roles are present, but not otherwise.
From Conjunctive Queries to Instance Queries in Ontology-Mediated Querying
Oct 22, 2020Abstract:We consider ontology-mediated queries (OMQs) based on expressive description logics of the ALC family and (unions) of conjunctive queries, studying the rewritability into OMQs based on instance queries (IQs). Our results include exact characterizations of when such a rewriting is possible and tight complexity bounds for deciding rewritability. We also give a tight complexity bound for the related problem of deciding whether a given MMSNP sentence is equivalent to a CSP.
Separating Positive and Negative Data Examples by Concepts and Formulas: The Case of Restricted Signatures
Jul 06, 2020Abstract:We study the separation of positive and negative data examples in terms of description logic (DL) concepts and formulas of decidable FO fragments, in the presence of an ontology. In contrast to previous work, we add a signature that specifies a subset of the symbols from the data and ontology that can be used for separation. We consider weak and strong versions of the resulting problem that differ in how the negative examples are treated. Our main results are that (a projective form of) the weak version is decidable in $\mathcal{ALCI}$ while it is undecidable in the guarded fragment GF, the guarded negation fragment GNF, and the DL $\mathcal{ALCFIO}$, and that strong separability is decidable in $\mathcal{ALCI}$, GF, and GNF. We also provide (mostly tight) complexity bounds.
Logical Separability of Incomplete Data under Ontologies
Jul 03, 2020
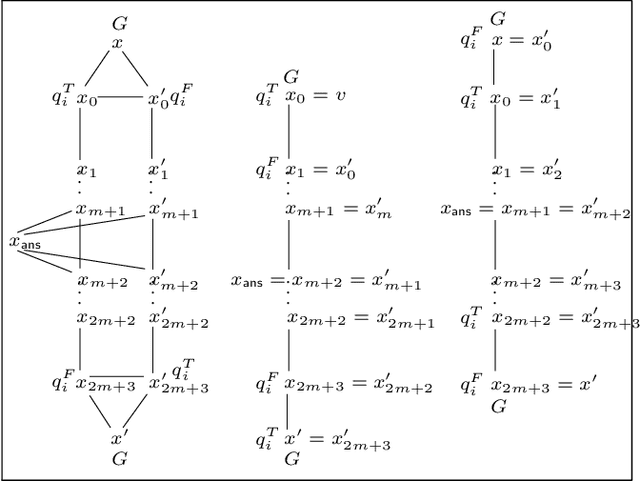
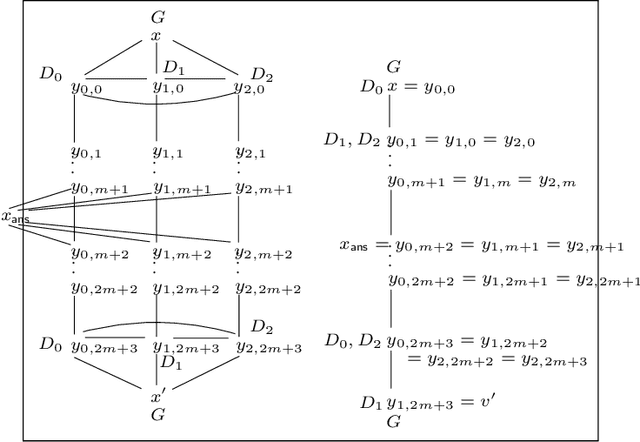
Abstract:Finding a logical formula that separates positive and negative examples given in the form of labeled data items is fundamental in applications such as concept learning, reverse engineering of database queries, and generating referring expressions. In this paper, we investigate the existence of a separating formula for incomplete data in the presence of an ontology. Both for the ontology language and the separation language, we concentrate on first-order logic and three important fragments thereof: the description logic $\mathcal{ALCI}$, the guarded fragment, and the two-variable fragment. We consider several forms of separability that differ in the treatment of negative examples and in whether or not they admit the use of additional helper symbols to achieve separation. We characterize separability in a model-theoretic way, compare the separating power of the different languages, and determine the computational complexity of separability as a decision problem.
A Journey into Ontology Approximation: From Non-Horn to Hon
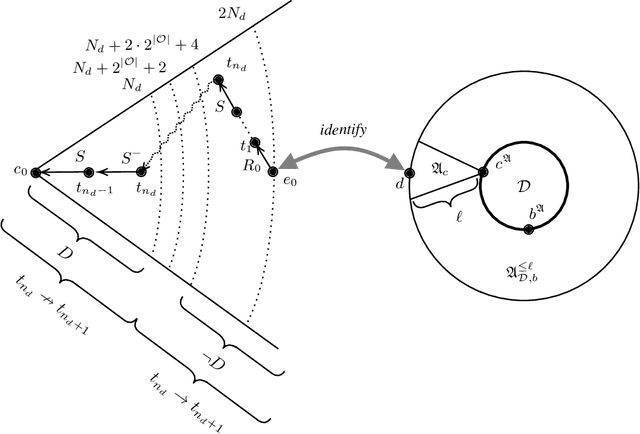
Jan 25, 2020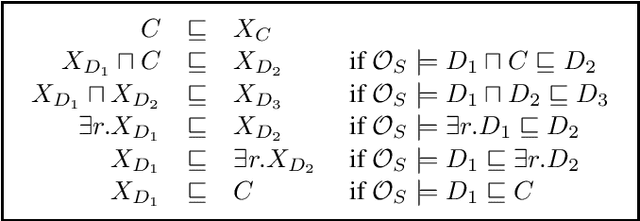
Abstract:We study complete approximations of an ontology formulated in a non-Horn description logic (DL) such as $\mathcal{ALC}$ in a Horn DL such as~$\mathcal{EL}$. We provide concrete approximation schemes that are necessarily infinite and observe that in the $\mathcal{ELU}$-to-$\mathcal{EL}$ case finite approximations tend to exist in practice and are guaranteed to exist when the original ontology is acyclic. In contrast, neither of this is the case for $\mathcal{ELU}_\bot$-to-$\mathcal{EL}_\bot$ and for $\mathcal{ALC}$-to-$\mathcal{EL}_\bot$ approximations. We also define a notion of approximation tailored towards ontology-mediated querying, connect it to subsumption-based approximations, and identify a case where finite approximations are guaranteed to exist.
Query Inseparability for ALC Ontologies
Jan 31, 2019
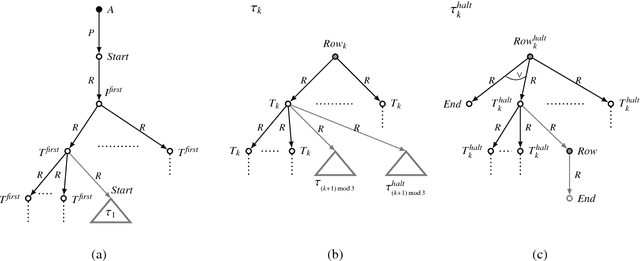

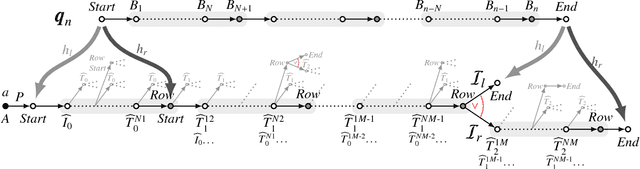
Abstract:We investigate the problem whether two ALC ontologies are indistinguishable (or inseparable) by means of queries in a given signature, which is fundamental for ontology engineering tasks such as ontology versioning, modularisation, update, and forgetting. We consider both knowledge base (KB) and TBox inseparability. For KBs, we give model-theoretic criteria in terms of (finite partial) homomorphisms and products and prove that this problem is undecidable for conjunctive queries (CQs), but 2ExpTime-complete for unions of CQs (UCQs). The same results hold if (U)CQs are replaced by rooted (U)CQs, where every variable is connected to an answer variable. We also show that inseparability by CQs is still undecidable if one KB is given in the lightweight DL EL and if no restrictions are imposed on the signature of the CQs. We also consider the problem whether two ALC TBoxes give the same answers to any query over any ABox in a given signature and show that, for CQs, this problem is undecidable, too. We then develop model-theoretic criteria for Horn-ALC TBoxes and show using tree automata that, in contrast, inseparability becomes decidable and 2ExpTime-complete, even ExpTime-complete when restricted to (unions of) rooted CQs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge