Elena Botoeva
Query Inseparability for ALC Ontologies
Jan 31, 2019
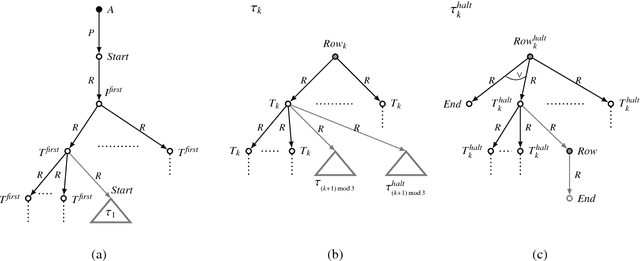

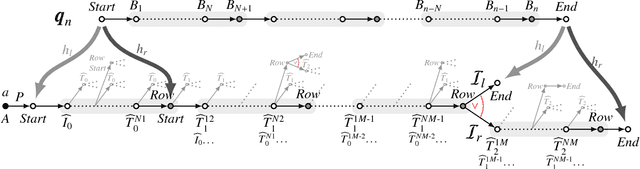
Abstract:We investigate the problem whether two ALC ontologies are indistinguishable (or inseparable) by means of queries in a given signature, which is fundamental for ontology engineering tasks such as ontology versioning, modularisation, update, and forgetting. We consider both knowledge base (KB) and TBox inseparability. For KBs, we give model-theoretic criteria in terms of (finite partial) homomorphisms and products and prove that this problem is undecidable for conjunctive queries (CQs), but 2ExpTime-complete for unions of CQs (UCQs). The same results hold if (U)CQs are replaced by rooted (U)CQs, where every variable is connected to an answer variable. We also show that inseparability by CQs is still undecidable if one KB is given in the lightweight DL EL and if no restrictions are imposed on the signature of the CQs. We also consider the problem whether two ALC TBoxes give the same answers to any query over any ABox in a given signature and show that, for CQs, this problem is undecidable, too. We then develop model-theoretic criteria for Horn-ALC TBoxes and show using tree automata that, in contrast, inseparability becomes decidable and 2ExpTime-complete, even ExpTime-complete when restricted to (unions of) rooted CQs.
Inseparability and Conservative Extensions of Description Logic Ontologies: A Survey
Apr 20, 2018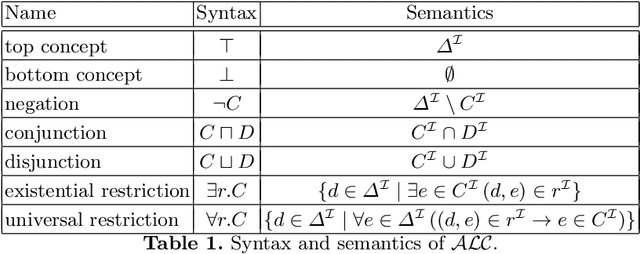
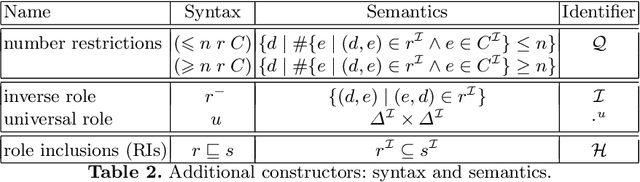
Abstract:The question whether an ontology can safely be replaced by another, possibly simpler, one is fundamental for many ontology engineering and maintenance tasks. It underpins, for example, ontology versioning, ontology modularization, forgetting, and knowledge exchange. What safe replacement means depends on the intended application of the ontology. If, for example, it is used to query data, then the answers to any relevant ontology-mediated query should be the same over any relevant data set; if, in contrast, the ontology is used for conceptual reasoning, then the entailed subsumptions between concept expressions should coincide. This gives rise to different notions of ontology inseparability such as query inseparability and concept inseparability, which generalize corresponding notions of conservative extensions. We survey results on various notions of inseparability in the context of description logic ontologies, discussing their applications, useful model-theoretic characterizations, algorithms for determining whether two ontologies are inseparable (and, sometimes, for computing the difference between them if they are not), and the computational complexity of this problem.
Beyond OWL 2 QL in OBDA: Rewritings and Approximations
Dec 01, 2015
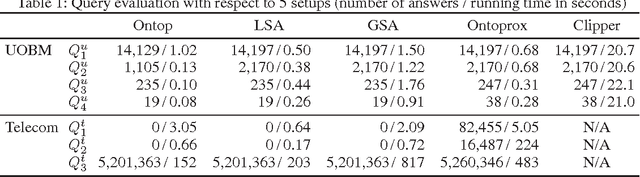
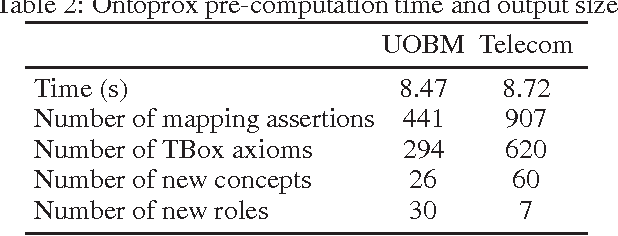
Abstract:Ontology-based data access (OBDA) is a novel paradigm facilitating access to relational data, realized by linking data sources to an ontology by means of declarative mappings. DL-Lite_R, which is the logic underpinning the W3C ontology language OWL 2 QL and the current language of choice for OBDA, has been designed with the goal of delegating query answering to the underlying database engine, and thus is restricted in expressive power. E.g., it does not allow one to express disjunctive information, and any form of recursion on the data. The aim of this paper is to overcome these limitations of DL-Lite_R, and extend OBDA to more expressive ontology languages, while still leveraging the underlying relational technology for query answering. We achieve this by relying on two well-known mechanisms, namely conservative rewriting and approximation, but significantly extend their practical impact by bringing into the picture the mapping, an essential component of OBDA. Specifically, we develop techniques to rewrite OBDA specifications with an expressive ontology to "equivalent" ones with a DL-Lite_R ontology, if possible, and to approximate them otherwise. We do so by exploiting the high expressive power of the mapping layer to capture part of the domain semantics of rich ontology languages. We have implemented our techniques in the prototype system OntoProx, making use of the state-of-the-art OBDA system Ontop and the query answering system Clipper, and we have shown their feasibility and effectiveness with experiments on synthetic and real-world data.
Exchanging OWL 2 QL Knowledge Bases
Jul 01, 2013
Abstract:Knowledge base exchange is an important problem in the area of data exchange and knowledge representation, where one is interested in exchanging information between a source and a target knowledge base connected through a mapping. In this paper, we study this fundamental problem for knowledge bases and mappings expressed in OWL 2 QL, the profile of OWL 2 based on the description logic DL-Lite_R. More specifically, we consider the problem of computing universal solutions, identified as one of the most desirable translations to be materialized, and the problem of computing UCQ-representations, which optimally capture in a target TBox the information that can be extracted from a source TBox and a mapping by means of unions of conjunctive queries. For the former we provide a novel automata-theoretic technique, and complexity results that range from NP to EXPTIME, while for the latter we show NLOGSPACE-completeness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge