Vladislav Ryzhikov
On Deciding the Data Complexity of Answering Linear Monadic Datalog Queries with LTL Operators(Extended Version)
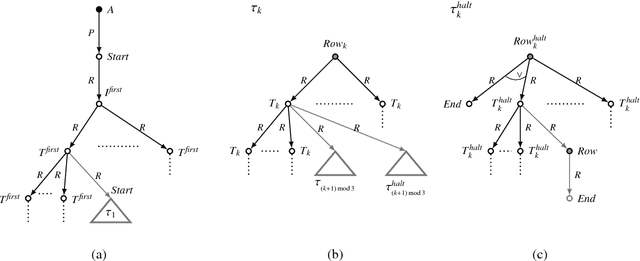
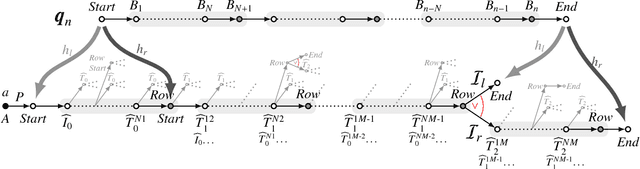
Jan 23, 2025Abstract:Our concern is the data complexity of answering linear monadic datalog queries whose atoms in the rule bodies can be prefixed by operators of linear temporal logic LTL. We first observe that, for data complexity, answering any connected query with operators $\bigcirc/\bigcirc^-$ (at the next/previous moment) is either in AC0, or in $ACC0\!\setminus\!AC0$, or $NC^1$-complete, or LogSpace-hard and in NLogSpace. Then we show that the problem of deciding LogSpace-hardness of answering such queries is PSpace-complete, while checking membership in the classes AC0 and ACC0 as well as $NC^1$-completeness can be done in ExpSpace. Finally, we prove that membership in AC0 or in ACC0, $NC^1$-completeness, and LogSpace-hardness are undecidable for queries with operators $\Diamond_f/\Diamond_p$ (sometime in the future/past) provided that $NC^1 \ne NLogSpace$, and $LogSpace \ne NLogSpace$.
Temporalising Unique Characterisability and Learnability of Ontology-Mediated Queries
Jun 13, 2023Abstract:Recently, the study of the unique characterisability and learnability of database queries by means of examples has been extended to ontology-mediated queries. Here, we study in how far the obtained results can be lifted to temporalised ontology-mediated queries. We provide a systematic introduction to the relevant approaches in the non-temporal case and then show general transfer results pinpointing under which conditions existing results can be lifted to temporalised queries.
Reverse Engineering of Temporal Queries Mediated by LTL Ontologies
May 04, 2023

Abstract:In reverse engineering of database queries, we aim to construct a query from a given set of answers and non-answers; it can then be used to explore the data further or as an explanation of the answers and non-answers. We investigate this query-by-example problem for queries formulated in positive fragments of linear temporal logic LTL over timestamped data, focusing on the design of suitable query languages and the combined and data complexity of deciding whether there exists a query in the given language that separates the given answers from non-answers. We consider both plain LTL queries and those mediated by LTL-ontologies.
Data Complexity and Rewritability of Ontology-Mediated Queries in Metric Temporal Logic under the Event-Based Semantics (Full Version)
May 30, 2019Abstract:We investigate the data complexity of answering queries mediated by metric temporal logic ontologies under the event-based semantics assuming that data instances are finite timed words timestamped with binary fractions. We identify classes of ontology-mediated queries answering which can be done in AC0, NC1, L, NL, P, and coNP for data complexity, provide their rewritings to first-order logic and its extensions with primitive recursion, transitive closure or datalog, and establish lower complexity bounds.
Query Inseparability for ALC Ontologies
Jan 31, 2019

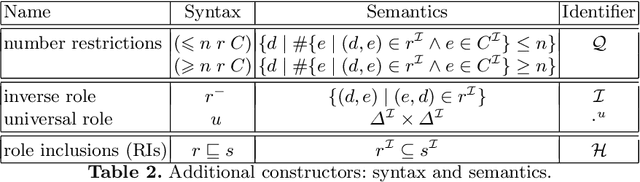
Abstract:We investigate the problem whether two ALC ontologies are indistinguishable (or inseparable) by means of queries in a given signature, which is fundamental for ontology engineering tasks such as ontology versioning, modularisation, update, and forgetting. We consider both knowledge base (KB) and TBox inseparability. For KBs, we give model-theoretic criteria in terms of (finite partial) homomorphisms and products and prove that this problem is undecidable for conjunctive queries (CQs), but 2ExpTime-complete for unions of CQs (UCQs). The same results hold if (U)CQs are replaced by rooted (U)CQs, where every variable is connected to an answer variable. We also show that inseparability by CQs is still undecidable if one KB is given in the lightweight DL EL and if no restrictions are imposed on the signature of the CQs. We also consider the problem whether two ALC TBoxes give the same answers to any query over any ABox in a given signature and show that, for CQs, this problem is undecidable, too. We then develop model-theoretic criteria for Horn-ALC TBoxes and show using tree automata that, in contrast, inseparability becomes decidable and 2ExpTime-complete, even ExpTime-complete when restricted to (unions of) rooted CQs.
Inseparability and Conservative Extensions of Description Logic Ontologies: A Survey
Apr 20, 2018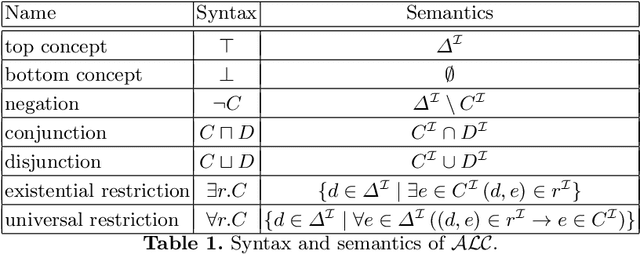
Abstract:The question whether an ontology can safely be replaced by another, possibly simpler, one is fundamental for many ontology engineering and maintenance tasks. It underpins, for example, ontology versioning, ontology modularization, forgetting, and knowledge exchange. What safe replacement means depends on the intended application of the ontology. If, for example, it is used to query data, then the answers to any relevant ontology-mediated query should be the same over any relevant data set; if, in contrast, the ontology is used for conceptual reasoning, then the entailed subsumptions between concept expressions should coincide. This gives rise to different notions of ontology inseparability such as query inseparability and concept inseparability, which generalize corresponding notions of conservative extensions. We survey results on various notions of inseparability in the context of description logic ontologies, discussing their applications, useful model-theoretic characterizations, algorithms for determining whether two ontologies are inseparable (and, sometimes, for computing the difference between them if they are not), and the computational complexity of this problem.
A Cookbook for Temporal Conceptual Data Modelling with Description Logics
May 02, 2014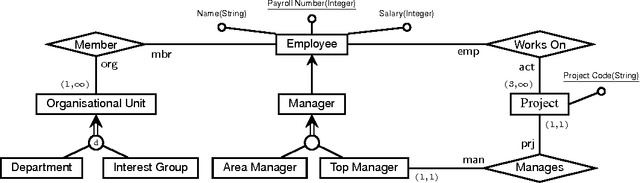
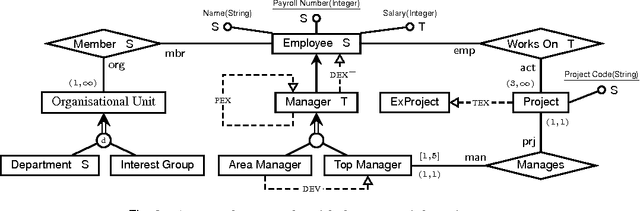
Abstract:We design temporal description logics suitable for reasoning about temporal conceptual data models and investigate their computational complexity. Our formalisms are based on DL-Lite logics with three types of concept inclusions (ranging from atomic concept inclusions and disjointness to the full Booleans), as well as cardinality constraints and role inclusions. In the temporal dimension, they capture future and past temporal operators on concepts, flexible and rigid roles, the operators `always' and `some time' on roles, data assertions for particular moments of time and global concept inclusions. The logics are interpreted over the Cartesian products of object domains and the flow of time (Z,<), satisfying the constant domain assumption. We prove that the most expressive of our temporal description logics (which can capture lifespan cardinalities and either qualitative or quantitative evolution constraints) turn out to be undecidable. However, by omitting some of the temporal operators on concepts/roles or by restricting the form of concept inclusions we obtain logics whose complexity ranges between PSpace and NLogSpace. These positive results were obtained by reduction to various clausal fragments of propositional temporal logic, which opens a way to employ propositional or first-order temporal provers for reasoning about temporal data models.
Exchanging OWL 2 QL Knowledge Bases
Jul 01, 2013
Abstract:Knowledge base exchange is an important problem in the area of data exchange and knowledge representation, where one is interested in exchanging information between a source and a target knowledge base connected through a mapping. In this paper, we study this fundamental problem for knowledge bases and mappings expressed in OWL 2 QL, the profile of OWL 2 based on the description logic DL-Lite_R. More specifically, we consider the problem of computing universal solutions, identified as one of the most desirable translations to be materialized, and the problem of computing UCQ-representations, which optimally capture in a target TBox the information that can be extracted from a source TBox and a mapping by means of unions of conjunctive queries. For the former we provide a novel automata-theoretic technique, and complexity results that range from NP to EXPTIME, while for the latter we show NLOGSPACE-completeness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge