Adding Circumscription to Decidable Fragments of First-Order Logic: A Complexity Rollercoaster

We study extensions of expressive decidable fragments of first-order logic with circumscription, in particular the two-variable fragment FO$^2$, its extension C$^2$ with counting quantifiers, and the guarded fragment GF. We prove that if only unary predicates are minimized (or fixed) during circumscription, then decidability of logical consequence is preserved. For FO$^2$ the complexity increases from $\textrm{coNexp}$ to $\textrm{coNExp}^\textrm{NP}$-complete, for GF it (remarkably!) increases from $\textrm{2Exp}$ to $\textrm{Tower}$-complete, and for C$^2$ the complexity remains open. We also consider querying circumscribed knowledge bases whose ontology is a GF sentence, showing that the problem is decidable for unions of conjunctive queries, $\textrm{Tower}$-complete in combined complexity, and elementary in data complexity. Already for atomic queries and ontologies that are sets of guarded existential rules, however, for every $k \geq 0$ there is an ontology and query that are $k$-$\textrm{Exp}$-hard in data complexity.

Logical Characterizations of Recurrent Graph Neural Networks with Reals and Floats

In pioneering work from 2019, Barcel\'o and coauthors identified logics that precisely match the expressive power of constant iteration-depth graph neural networks (GNNs) relative to properties definable in first-order logic. In this article, we give exact logical characterizations of recurrent GNNs in two scenarios: (1) in the setting with floating-point numbers and (2) with reals. For floats, the formalism matching recurrent GNNs is a rule-based modal logic with counting, while for reals we use a suitable infinitary modal logic, also with counting. These results give exact matches between logics and GNNs in the recurrent setting without relativising to a background logic in either case, but using some natural assumptions about floating-point arithmetic. Applying our characterizations, we also prove that, relative to graph properties definable in monadic second-order logic (MSO), our infinitary and rule-based logics are equally expressive. This implies that recurrent GNNs with reals and floats have the same expressive power over MSO-definable properties and shows that, for such properties, also recurrent GNNs with reals are characterized by a (finitary!) rule-based modal logic. In the general case, in contrast, the expressive power with floats is weaker than with reals. In addition to logic-oriented results, we also characterize recurrent GNNs, with both reals and floats, via distributed automata, drawing links to distributed computing models.

Towards Ontology Construction with Language Models

We present a method for automatically constructing a concept hierarchy for a given domain by querying a large language model. We apply this method to various domains using OpenAI's GPT 3.5. Our experiments indicate that LLMs can be of considerable help for constructing concept hierarchies.

Querying Circumscribed Description Logic Knowledge Bases

Circumscription is one of the main approaches for defining non-monotonic description logics (DLs). While the decidability and complexity of traditional reasoning tasks such as satisfiability of circumscribed DL knowledge bases (KBs) is well understood, for evaluating conjunctive queries (CQs) and unions thereof (UCQs), not even decidability had been established. In this paper, we prove decidability of (U)CQ evaluation on circumscribed DL KBs and obtain a rather complete picture of both the combined complexity and the data complexity, for DLs ranging from ALCHIO via EL to various versions of DL-Lite. We also study the much simpler atomic queries (AQs).

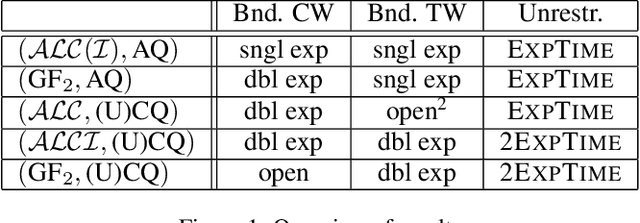
Description Logics with Abstraction and Refinement

Ontologies often require knowledge representation on multiple levels of abstraction, but description logics (DLs) are not well-equipped for supporting this. We propose an extension of DLs in which abstraction levels are first-class citizens and which provides explicit operators for the abstraction and refinement of concepts and roles across multiple abstraction levels, based on conjunctive queries. We prove that reasoning in the resulting family of DLs is decidable while several seemingly harmless variations turn out to be undecidable. We also pinpoint the precise complexity of our logics and several relevant fragments.

SAT-Based PAC Learning of Description Logic Concepts

We propose bounded fitting as a scheme for learning description logic concepts in the presence of ontologies. A main advantage is that the resulting learning algorithms come with theoretical guarantees regarding their generalization to unseen examples in the sense of PAC learning. We prove that, in contrast, several other natural learning algorithms fail to provide such guarantees. As a further contribution, we present the system SPELL which efficiently implements bounded fitting for the description logic $\mathcal{ELH}^r$ based on a SAT solver, and compare its performance to a state-of-the-art learner.

On the non-efficient PAC learnability of acyclic conjunctive queries

This note serves three purposes: (i) we provide a self-contained exposition of the fact that conjunctive queries are not efficiently learnable in the Probably-Approximately-Correct (PAC) model, paying clear attention to the complicating fact that this concept class lacks the polynomial-size fitting property, a property that is tacitly assumed in much of the computational learning theory literature; (ii) we establish a strong negative PAC learnability result that applies to many restricted classes of conjunctive queries (CQs), including acyclic CQs for a wide range of notions of "acyclicity"; (iii) we show that CQs are efficiently PAC learnable with membership queries.

Ontology-Mediated Querying on Databases of Bounded Cliquewidth

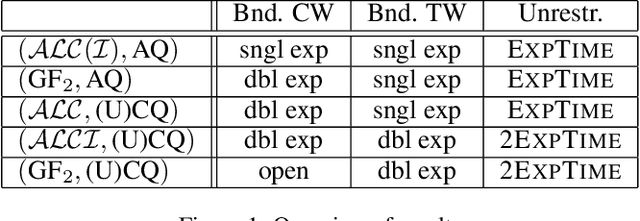
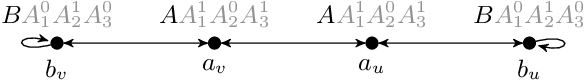
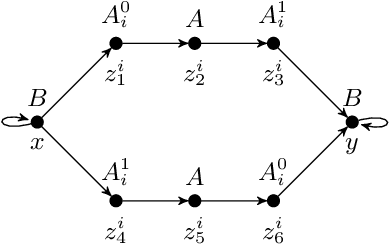
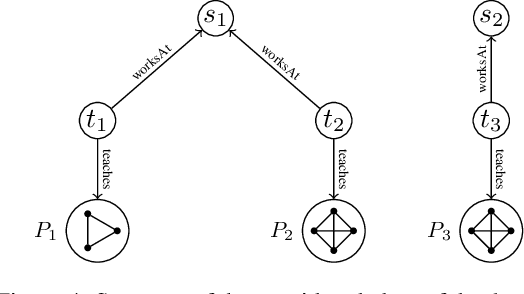
We study the evaluation of ontology-mediated queries (OMQs) on databases of bounded cliquewidth from the viewpoint of parameterized complexity theory. As the ontology language, we consider the description logics $\mathcal{ALC}$ and $\mathcal{ALCI}$ as well as the guarded two-variable fragment GF$_2$ of first-order logic. Queries are atomic queries (AQs), conjunctive queries (CQs), and unions of CQs. All studied OMQ problems are fixed-parameter linear (FPL) when the parameter is the size of the OMQ plus the cliquewidth. Our main contribution is a detailed analysis of the dependence of the running time on the parameter, exhibiting several interesting effects.

Frontiers and Exact Learning of ELI Queries under DL-Lite Ontologies

We study ELI queries (ELIQs) in the presence of ontologies formulated in the description logic DL-Lite. For the dialect DL-LiteH, we show that ELIQs have a frontier (set of least general generalizations) that is of polynomial size and can be computed in polynomial time. In the dialect DL-LiteF, in contrast, frontiers may be infinite. We identify a natural syntactic restriction that enables the same positive results as for DL-LiteH. We use out results on frontiers to show that ELIQs are learnable in polynomial time in the presence of a DL-LiteH / restricted DL-LiteF ontology in Angluin's framework of exact learning with only membership queries.

Conservative Extensions for Existential Rules

We study the problem to decide, given sets T1,T2 of tuple-generating dependencies (TGDs), also called existential rules, whether T2 is a conservative extension of T1. We consider two natural notions of conservative extension, one pertaining to answers to conjunctive queries over databases and one to homomorphisms between chased databases. Our main results are that these problems are undecidable for linear TGDs, undecidable for guarded TGDs even when T1 is empty, and decidable for frontier-one TGDs.