Globally Interpretable Classifiers via Boolean Formulas with Dynamic Propositions

Interpretability and explainability are among the most important challenges of modern artificial intelligence, being mentioned even in various legislative sources. In this article, we develop a method for extracting immediately human interpretable classifiers from tabular data. The classifiers are given in the form of short Boolean formulas built with propositions that can either be directly extracted from categorical attributes or dynamically computed from numeric ones. Our method is implemented using Answer Set Programming. We investigate seven datasets and compare our results to ones obtainable by state-of-the-art classifiers for tabular data, namely, XGBoost and random forests. Over all datasets, the accuracies obtainable by our method are similar to the reference methods. The advantage of our classifiers in all cases is that they are very short and immediately human intelligible as opposed to the black-box nature of the reference methods.

Logical Characterizations of Recurrent Graph Neural Networks with Reals and Floats

In pioneering work from 2019, Barcel\'o and coauthors identified logics that precisely match the expressive power of constant iteration-depth graph neural networks (GNNs) relative to properties definable in first-order logic. In this article, we give exact logical characterizations of recurrent GNNs in two scenarios: (1) in the setting with floating-point numbers and (2) with reals. For floats, the formalism matching recurrent GNNs is a rule-based modal logic with counting, while for reals we use a suitable infinitary modal logic, also with counting. These results give exact matches between logics and GNNs in the recurrent setting without relativising to a background logic in either case, but using some natural assumptions about floating-point arithmetic. Applying our characterizations, we also prove that, relative to graph properties definable in monadic second-order logic (MSO), our infinitary and rule-based logics are equally expressive. This implies that recurrent GNNs with reals and floats have the same expressive power over MSO-definable properties and shows that, for such properties, also recurrent GNNs with reals are characterized by a (finitary!) rule-based modal logic. In the general case, in contrast, the expressive power with floats is weaker than with reals. In addition to logic-oriented results, we also characterize recurrent GNNs, with both reals and floats, via distributed automata, drawing links to distributed computing models.

Interpretable classifiers for tabular data via discretization and feature selection

We introduce a method for computing immediately human interpretable yet accurate classifiers from tabular data. The classifiers obtained are short DNF-formulas, computed via first discretizing the original data to Boolean form and then using feature selection coupled with a very fast algorithm for producing the best possible Boolean classifier for the setting. We demonstrate the approach via 14 experiments, obtaining results with accuracies mainly similar to ones obtained via random forests, XGBoost, and existing results for the same datasets in the literature. In several cases, our approach in fact outperforms the reference results in relation to accuracy, even though the main objective of our study is the immediate interpretability of our classifiers. We also prove a new result on the probability that the classifier we obtain from real-life data corresponds to the ideally best classifier with respect to the background distribution the data comes from.

Short Boolean Formulas as Explanations in Practice

We investigate explainability via short Boolean formulas in the data model based on unary relations. As an explanation of length k, we take a Boolean formula of length k that minimizes the error with respect to the target attribute to be explained. We first provide novel quantitative bounds for the expected error in this scenario. We then also demonstrate how the setting works in practice by studying three concrete data sets. In each case, we calculate explanation formulas of different lengths using an encoding in Answer Set Programming. The most accurate formulas we obtain achieve errors similar to other methods on the same data sets. However, due to overfitting, these formulas are not necessarily ideal explanations, so we use cross validation to identify a suitable length for explanations. By limiting to shorter formulas, we obtain explanations that avoid overfitting but are still reasonably accurate and also, importantly, human interpretable.

Explainability via Short Formulas: the Case of Propositional Logic with Implementation

We conceptualize explainability in terms of logic and formula size, giving a number of related definitions of explainability in a very general setting. Our main interest is the so-called special explanation problem which aims to explain the truth value of an input formula in an input model. The explanation is a formula of minimal size that (1) agrees with the input formula on the input model and (2) transmits the involved truth value to the input formula globally, i.e., on every model. As an important example case, we study propositional logic in this setting and show that the special explainability problem is complete for the second level of the polynomial hierarchy. We also provide an implementation of this problem in answer set programming and investigate its capacity in relation to explaining answers to the n-queens and dominating set problems.

Rational coordination with no communication or conventions

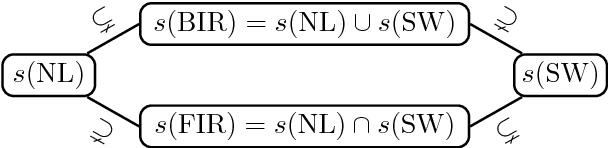
We study pure coordination games where in every outcome, all players have identical payoffs, 'win' or 'lose'. We identify and discuss a range of 'purely rational principles' guiding the reasoning of rational players in such games and analyze which classes of coordination games can be solved by such players with no preplay communication or conventions. We observe that it is highly nontrivial to delineate a boundary between purely rational principles and other decision methods, such as conventions, for solving such coordination games.

On the uniform one-dimensional fragment

The uniform one-dimensional fragment of first-order logic, U1, is a recently introduced formalism that extends two-variable logic in a natural way to contexts with relations of all arities. We survey properties of U1 and investigate its relationship to description logics designed to accommodate higher arity relations, with particular attention given to DLR_reg. We also define a description logic version of a variant of U1 and prove a range of new results concerning the expressivity of U1 and related logics.