A Logic for Conditional Local Strategic Reasoning

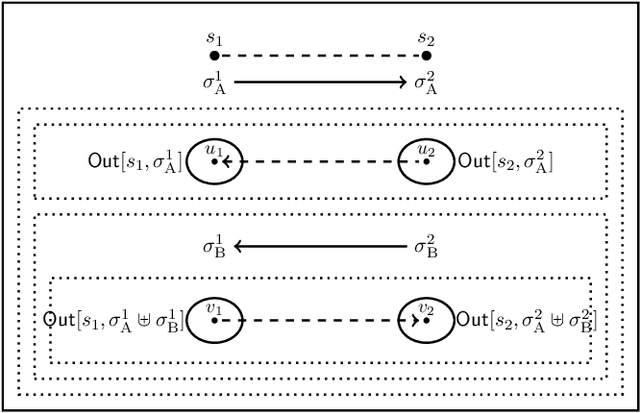
We consider systems of rational agents who act and interact in pursuit of their individual and collective objectives. We study and formalise the reasoning of an agent, or of an external observer, about the expected choices of action of the other agents based on their objectives, in order to assess the reasoner's ability, or expectation, to achieve their own objective. To formalize such reasoning we extend Pauly's Coalition Logic with three new modal operators of conditional strategic reasoning, thus introducing the Logic for Local Conditional Strategic Reasoning ConStR. We provide formal semantics for the new conditional strategic operators in concurrent game models, introduce the matching notion of bisimulation for each of them, prove bisimulation invariance and Hennessy-Milner property for each of them, and discuss and compare briefly their expressiveness. Finally, we also propose systems of axioms for each of the basic operators of ConStR and for the full logic.

Rational coordination with no communication or conventions

We study pure coordination games where in every outcome, all players have identical payoffs, 'win' or 'lose'. We identify and discuss a range of 'purely rational principles' guiding the reasoning of rational players in such games and analyze which classes of coordination games can be solved by such players with no preplay communication or conventions. We observe that it is highly nontrivial to delineate a boundary between purely rational principles and other decision methods, such as conventions, for solving such coordination games.

Tableau-based decision procedure for the multi-agent epistemic logic with all coalitional operators for common and distributed knowledge

We develop a conceptually clear, intuitive, and feasible decision procedure for testing satisfiability in the full multi-agent epistemic logic CMAEL(CD) with operators for common and distributed knowledge for all coalitions of agents mentioned in the language. To that end, we introduce Hintikka structures for CMAEL(CD) and prove that satisfiability in such structures is equivalent to satisfiability in standard models. Using that result, we design an incremental tableau-building procedure that eventually constructs a satisfying Hintikka structure for every satisfiable input set of formulae of CMAEL(CD) and closes for every unsatisfiable input set of formulae.

Tableau-based decision procedures for logics of strategic ability in multi-agent systems

We develop an incremental tableau-based decision procedures for the Alternating-time temporal logic ATL and some of its variants. While running within the theoretically established complexity upper bound, we claim that our tableau is practically more efficient in the average case than other decision procedures for ATL known so far. Besides, the ease of its adaptation to variants of ATL demonstrates the flexibility of the proposed procedure.