Globally Interpretable Classifiers via Boolean Formulas with Dynamic Propositions

Interpretability and explainability are among the most important challenges of modern artificial intelligence, being mentioned even in various legislative sources. In this article, we develop a method for extracting immediately human interpretable classifiers from tabular data. The classifiers are given in the form of short Boolean formulas built with propositions that can either be directly extracted from categorical attributes or dynamically computed from numeric ones. Our method is implemented using Answer Set Programming. We investigate seven datasets and compare our results to ones obtainable by state-of-the-art classifiers for tabular data, namely, XGBoost and random forests. Over all datasets, the accuracies obtainable by our method are similar to the reference methods. The advantage of our classifiers in all cases is that they are very short and immediately human intelligible as opposed to the black-box nature of the reference methods.

Interpretable classifiers for tabular data via discretization and feature selection

We introduce a method for computing immediately human interpretable yet accurate classifiers from tabular data. The classifiers obtained are short DNF-formulas, computed via first discretizing the original data to Boolean form and then using feature selection coupled with a very fast algorithm for producing the best possible Boolean classifier for the setting. We demonstrate the approach via 14 experiments, obtaining results with accuracies mainly similar to ones obtained via random forests, XGBoost, and existing results for the same datasets in the literature. In several cases, our approach in fact outperforms the reference results in relation to accuracy, even though the main objective of our study is the immediate interpretability of our classifiers. We also prove a new result on the probability that the classifier we obtain from real-life data corresponds to the ideally best classifier with respect to the background distribution the data comes from.

Short Boolean Formulas as Explanations in Practice

We investigate explainability via short Boolean formulas in the data model based on unary relations. As an explanation of length k, we take a Boolean formula of length k that minimizes the error with respect to the target attribute to be explained. We first provide novel quantitative bounds for the expected error in this scenario. We then also demonstrate how the setting works in practice by studying three concrete data sets. In each case, we calculate explanation formulas of different lengths using an encoding in Answer Set Programming. The most accurate formulas we obtain achieve errors similar to other methods on the same data sets. However, due to overfitting, these formulas are not necessarily ideal explanations, so we use cross validation to identify a suitable length for explanations. By limiting to shorter formulas, we obtain explanations that avoid overfitting but are still reasonably accurate and also, importantly, human interpretable.

Capturing (Optimal) Relaxed Plans with Stable and Supported Models of Logic Programs

We establish a novel relation between delete-free planning, an important task for the AI Planning community also known as relaxed planning, and logic programming. We show that given a planning problem, all subsets of actions that could be ordered to produce relaxed plans for the problem can be bijectively captured with stable models of a logic program describing the corresponding relaxed planning problem. We also consider the supported model semantics of logic programs, and introduce one causal and one diagnostic encoding of the relaxed planning problem as logic programs, both capturing relaxed plans with their supported models. Our experimental results show that these new encodings can provide major performance gain when computing optimal relaxed plans, with our diagnostic encoding outperforming state-of-the-art approaches to relaxed planning regardless of the given time limit when measured on a wide collection of STRIPS planning benchmarks.

Explainability via Short Formulas: the Case of Propositional Logic with Implementation

We conceptualize explainability in terms of logic and formula size, giving a number of related definitions of explainability in a very general setting. Our main interest is the so-called special explanation problem which aims to explain the truth value of an input formula in an input model. The explanation is a formula of minimal size that (1) agrees with the input formula on the input model and (2) transmits the involved truth value to the input formula globally, i.e., on every model. As an important example case, we study propositional logic in this setting and show that the special explainability problem is complete for the second level of the polynomial hierarchy. We also provide an implementation of this problem in answer set programming and investigate its capacity in relation to explaining answers to the n-queens and dominating set problems.

Propositional Encodings of Acyclicity and Reachability by using Vertex Elimination

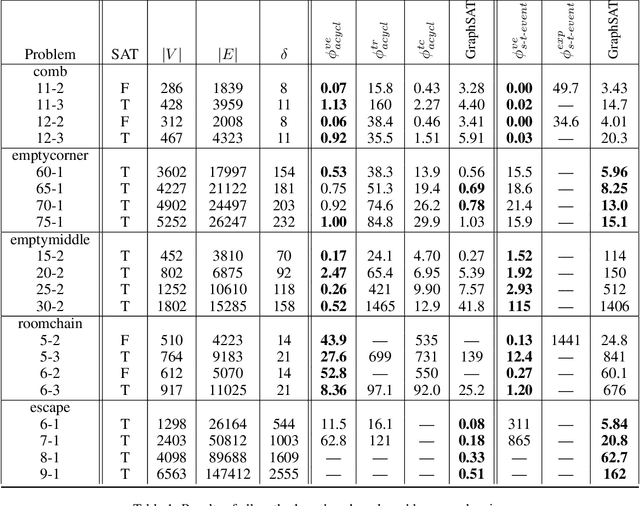
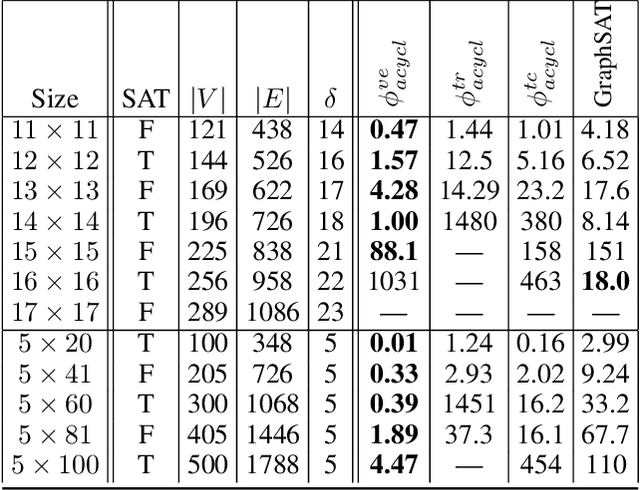
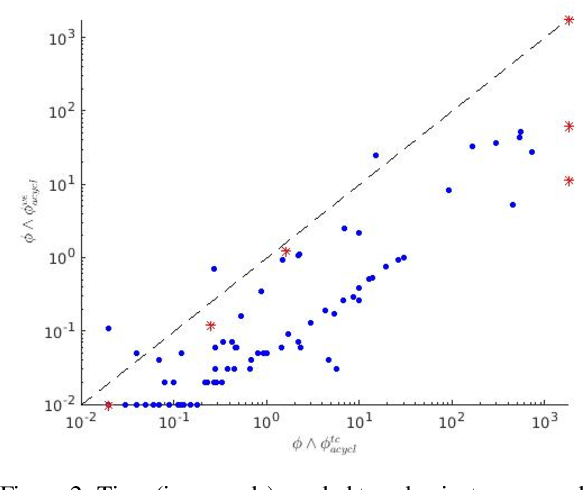
We introduce novel methods for encoding acyclicity and s-t-reachability constraints for propositional formulas with underlying directed graphs. They are based on vertex elimination graphs, which makes them suitable for cases where the underlying graph is sparse. In contrast to solvers with ad hoc constraint propagators for acyclicity and reachability constraints such as GraphSAT, our methods encode these constraints as standard propositional clauses, making them directly applicable with any SAT solver. An empirical study demonstrates that our methods together with an efficient SAT solver can outperform both earlier encodings of these constraints as well as GraphSAT, particularly when underlying graphs are sparse.