Planning with Complex Data Types in PDDL

Practically all of the planning research is limited to states represented in terms of Boolean and numeric state variables. Many practical problems, for example, planning inside complex software systems, require far more complex data types, and even real-world planning in many cases requires concepts such as sets of objects, which are not convenient to express in modeling languages with scalar types only. In this work, we investigate a modeling language for complex software systems, which supports complex data types such as sets, arrays, records, and unions. We give a reduction of a broad range of complex data types and their operations to Boolean logic, and then map this representation further to PDDL to be used with domain-independent PDDL planners. We evaluate the practicality of this approach, and provide solutions to some of the issues that arise in the PDDL translation.

Propositional Encodings of Acyclicity and Reachability by using Vertex Elimination

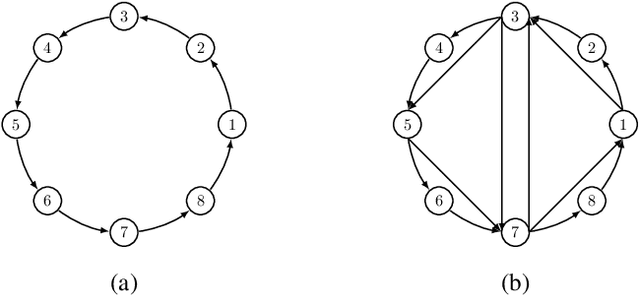
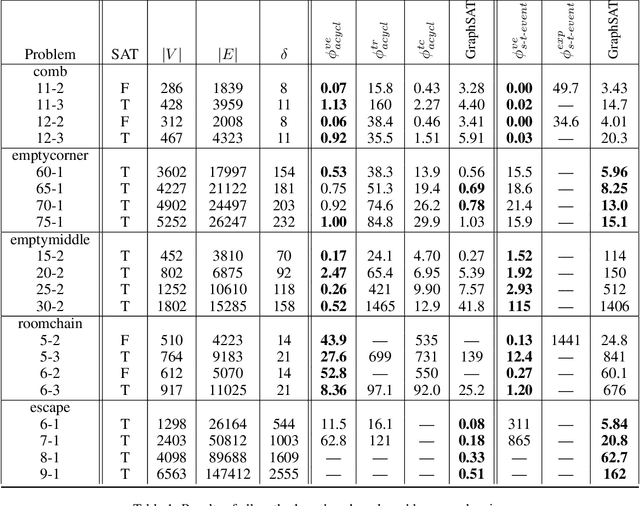
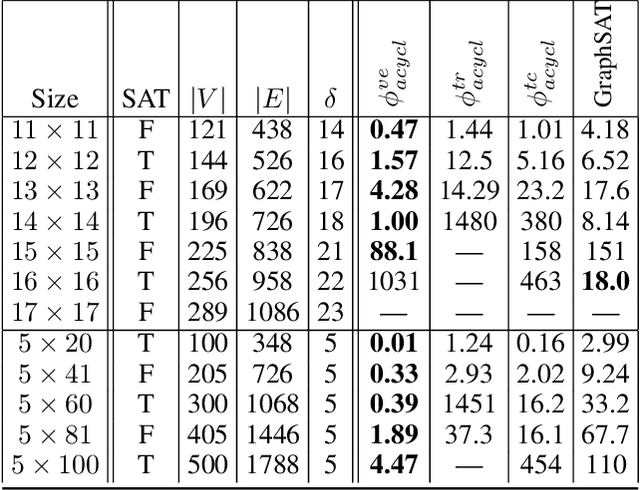
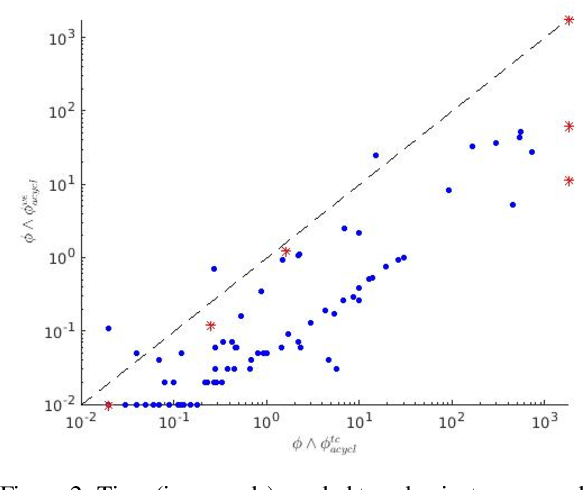
We introduce novel methods for encoding acyclicity and s-t-reachability constraints for propositional formulas with underlying directed graphs. They are based on vertex elimination graphs, which makes them suitable for cases where the underlying graph is sparse. In contrast to solvers with ad hoc constraint propagators for acyclicity and reachability constraints such as GraphSAT, our methods encode these constraints as standard propositional clauses, making them directly applicable with any SAT solver. An empirical study demonstrates that our methods together with an efficient SAT solver can outperform both earlier encodings of these constraints as well as GraphSAT, particularly when underlying graphs are sparse.

Learning Chordal Markov Networks by Constraint Satisfaction

We investigate the problem of learning the structure of a Markov network from data. It is shown that the structure of such networks can be described in terms of constraints which enables the use of existing solver technology with optimization capabilities to compute optimal networks starting from initial scores computed from the data. To achieve efficient encodings, we develop a novel characterization of Markov network structure using a balancing condition on the separators between cliques forming the network. The resulting translations into propositional satisfiability and its extensions such as maximum satisfiability, satisfiability modulo theories, and answer set programming, enable us to prove optimal certain network structures which have been previously found by stochastic search.