Likelihood-free Model Choice for Simulator-based Models with the Jensen--Shannon Divergence

Choice of appropriate structure and parametric dimension of a model in the light of data has a rich history in statistical research, where the first seminal approaches were developed in 1970s, such as the Akaike's and Schwarz's model scoring criteria that were inspired by information theory and embodied the rationale called Occam's razor. After those pioneering works, model choice was quickly established as its own field of research, gaining considerable attention in both computer science and statistics. However, to date, there have been limited attempts to derive scoring criteria for simulator-based models lacking a likelihood expression. Bayes factors have been considered for such models, but arguments have been put both for and against use of them and around issues related to their consistency. Here we use the asymptotic properties of Jensen--Shannon divergence (JSD) to derive a consistent model scoring criterion for the likelihood-free setting called JSD-Razor. Relationships of JSD-Razor with established scoring criteria for the likelihood-based approach are analyzed and we demonstrate the favorable properties of our criterion using both synthetic and real modeling examples.

Nonparametric likelihood-free inference with Jensen-Shannon divergence for simulator-based models with categorical output

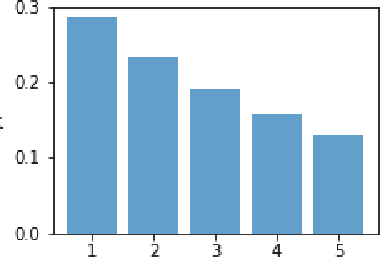
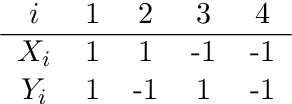
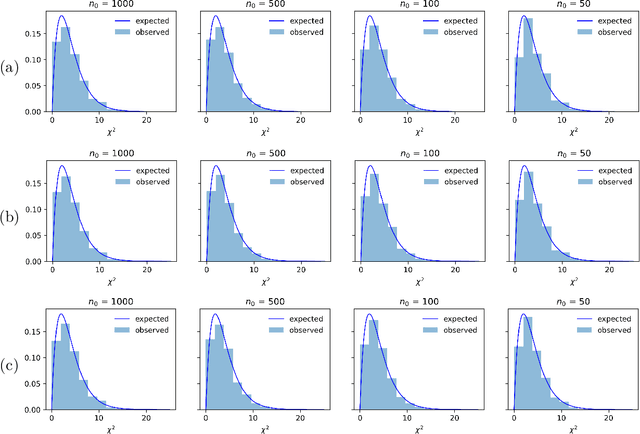
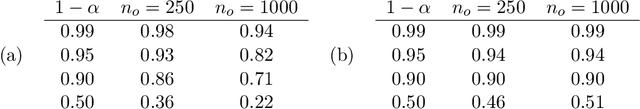
Likelihood-free inference for simulator-based statistical models has recently attracted a surge of interest, both in the machine learning and statistics communities. The primary focus of these research fields has been to approximate the posterior distribution of model parameters, either by various types of Monte Carlo sampling algorithms or deep neural network -based surrogate models. Frequentist inference for simulator-based models has been given much less attention to date, despite that it would be particularly amenable to applications with big data where implicit asymptotic approximation of the likelihood is expected to be accurate and can leverage computationally efficient strategies. Here we derive a set of theoretical results to enable estimation, hypothesis testing and construction of confidence intervals for model parameters using asymptotic properties of the Jensen--Shannon divergence. Such asymptotic approximation offers a rapid alternative to more computation-intensive approaches and can be attractive for diverse applications of simulator-based models. 61

T-SNE Is Not Optimized to Reveal Clusters in Data

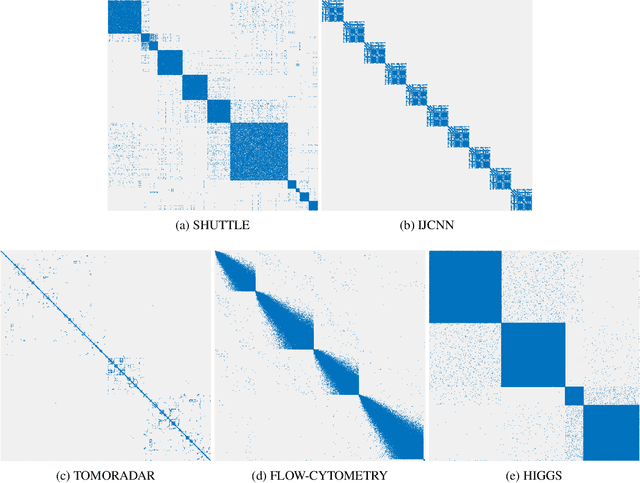
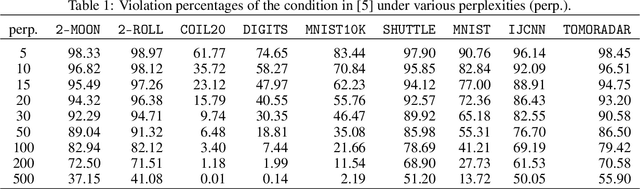
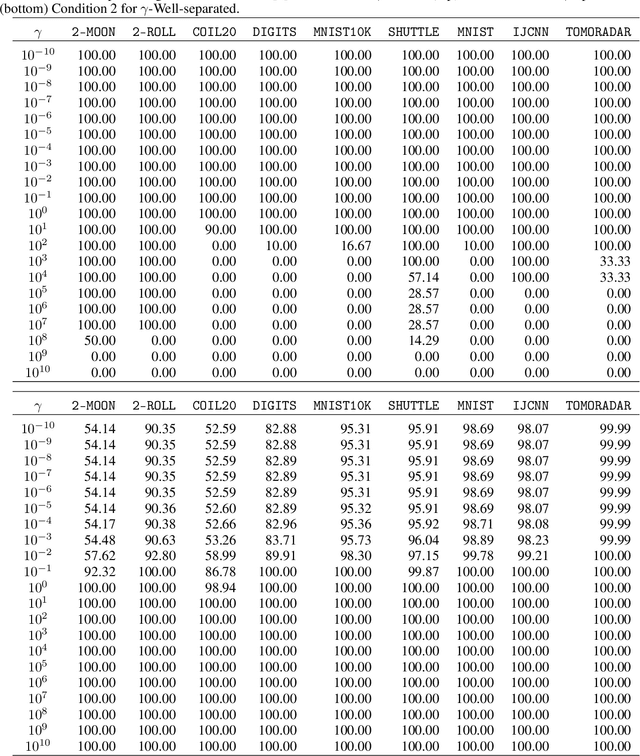
Cluster visualization is an essential task for nonlinear dimensionality reduction as a data analysis tool. It is often believed that Student t-Distributed Stochastic Neighbor Embedding (t-SNE) can show clusters for well clusterable data, with a smaller Kullback-Leibler divergence corresponding to a better quality. There was even theoretical proof for the guarantee of this property. However, we point out that this is not necessarily the case -- t-SNE may leave clustering patterns hidden despite strong signals present in the data. Extensive empirical evidence is provided to support our claim. First, several real-world counter-examples are presented, where t-SNE fails even if the input neighborhoods are well clusterable. Tuning hyperparameters in t-SNE or using better optimization algorithms does not help solve this issue because a better t-SNE learning objective can correspond to a worse cluster embedding. Second, we check the assumptions in the clustering guarantee of t-SNE and find they are often violated for real-world data sets.

Stochastic Cluster Embedding

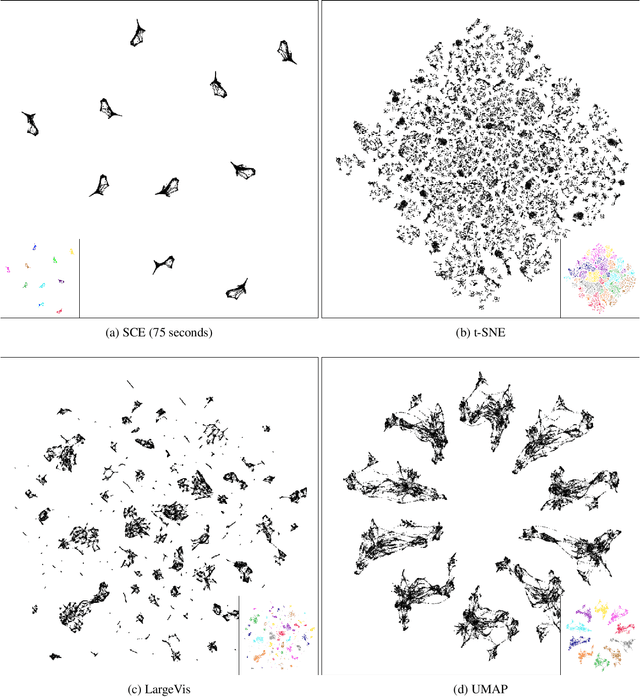
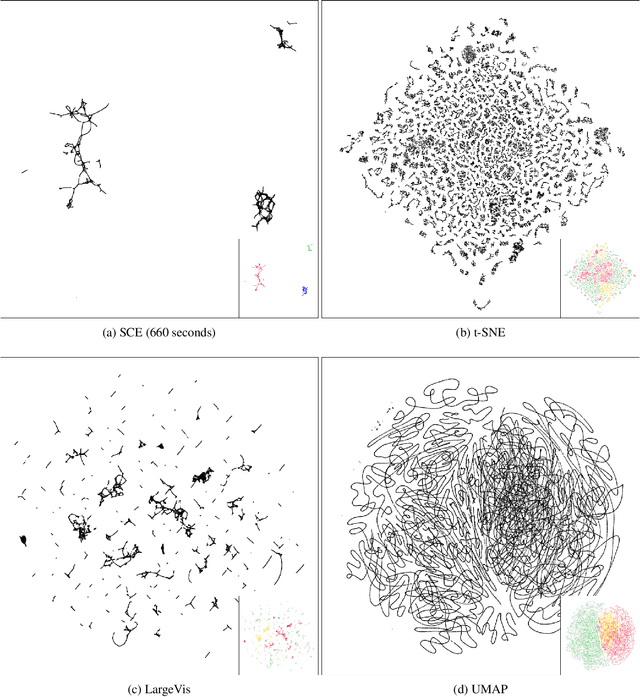
Neighbor Embedding (NE) that aims to preserve pairwise similarities between data items has been shown to yield an effective principle for data visualization. However, even the currently best NE methods such as Stochastic Neighbor Embedding (SNE) may leave large-scale patterns such as clusters hidden despite of strong signals being present in the data. To address this, we propose a new cluster visualization method based on Neighbor Embedding. We first present a family of Neighbor Embedding methods which generalizes SNE by using non-normalized Kullback-Leibler divergence with a scale parameter. In this family, much better cluster visualizations often appear with a parameter value different from the one corresponding to SNE. We also develop an efficient software which employs asynchronous stochastic block coordinate descent to optimize the new family of objective functions. The experimental results demonstrate that our method consistently and substantially improves visualization of data clusters compared with the state-of-the-art NE approaches.

Approximate Bayesian inference from noisy likelihoods with Gaussian process emulated MCMC

We present an efficient approach for doing approximate Bayesian inference when only a limited number of noisy likelihood evaluations can be obtained due to computational constraints, which is becoming increasingly common for applications of complex models. Our main methodological innovation is to model the log-likelihood function using a Gaussian process (GP) in a local fashion and apply this model to emulate the progression that an exact Metropolis-Hastings (MH) algorithm would take if it was applicable. New log-likelihood evaluation locations are selected using sequential experimental design strategies such that each MH accept/reject decision is done within a pre-specified error tolerance. The resulting approach is conceptually simple and sample-efficient as it takes full advantage of the GP model. It is also more robust to violations of GP modelling assumptions and better suited for the typical situation where the posterior is substantially more concentrated than the prior, compared with various existing inference methods based on global GP surrogate modelling. We discuss the probabilistic interpretations and central theoretical aspects of our approach, and we then demonstrate the benefits of the resulting algorithm in the context of likelihood-free inference for simulator-based statistical models.

Structure Learning of Contextual Markov Networks using Marginal Pseudo-likelihood

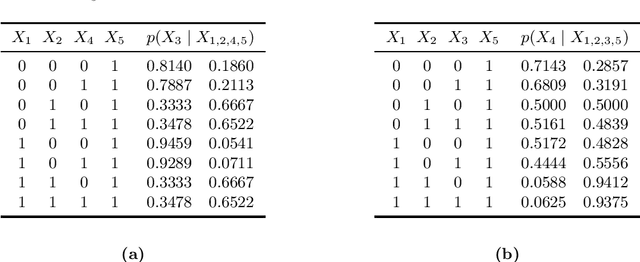
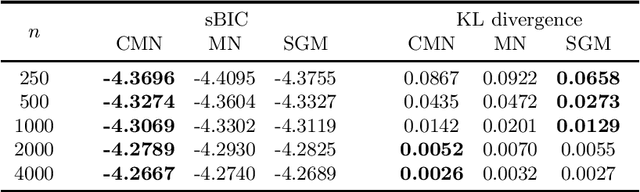
Markov networks are popular models for discrete multivariate systems where the dependence structure of the variables is specified by an undirected graph. To allow for more expressive dependence structures, several generalizations of Markov networks have been proposed. Here we consider the class of contextual Markov networks which takes into account possible context-specific independences among pairs of variables. Structure learning of contextual Markov networks is very challenging due to the extremely large number of possible structures. One of the main challenges has been to design a score, by which a structure can be assessed in terms of model fit related to complexity, without assuming chordality. Here we introduce the marginal pseudo-likelihood as an analytically tractable criterion for general contextual Markov networks. Our criterion is shown to yield a consistent structure estimator. Experiments demonstrate the favorable properties of our method in terms of predictive accuracy of the inferred models.

Likelihood-Free Inference with Deep Gaussian Processes

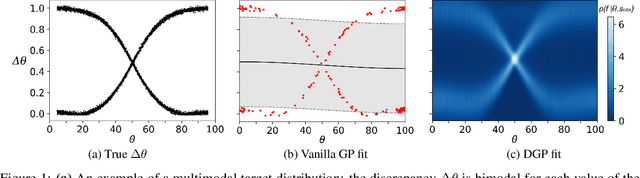
In recent years, surrogate models have been successfully used in likelihood-free inference to decrease the number of simulator evaluations. The current state-of-the-art performance for this task has been achieved by Bayesian Optimization with Gaussian Processes (GPs). While this combination works well for unimodal target distributions, it is restricting the flexibility and applicability of Bayesian Optimization for accelerating likelihood-free inference more generally. We address this problem by proposing a Deep Gaussian Process (DGP) surrogate model that can handle more irregularly behaved target distributions. Our experiments show how DGPs can outperform GPs on objective functions with multimodal distributions and maintain a comparable performance in unimodal cases. This confirms that DGPs as surrogate models can extend the applicability of Bayesian Optimization for likelihood-free inference (BOLFI), while adding computational overhead that remains negligible for computationally intensive simulators.

Split-BOLFI for for misspecification-robust likelihood free inference in high dimensions

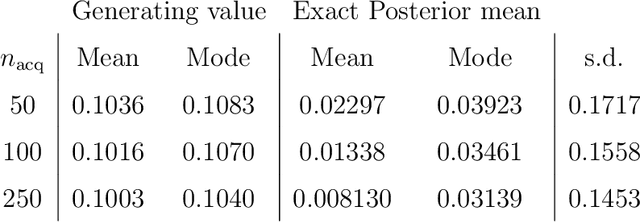
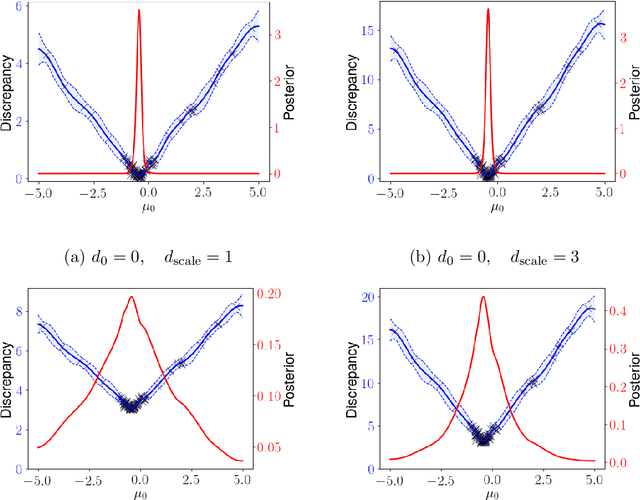
Likelihood-free inference for simulator-based statistical models has recently grown rapidly from its infancy to a useful tool for practitioners. However, models with more than a very small number of parameters as the target of inference have remained an enigma, in particular for the approximate Bayesian computation (ABC) community. To advance the possibilities for performing likelihood-free inference in high-dimensional parameter spaces, here we introduce an extension of the popular Bayesian optimisation based approach to approximate discrepancy functions in a probabilistic manner which lends itself to an efficient exploration of the parameter space. Our method achieves computational scalability by using separate acquisition procedures for the discrepancies defined for different parameters. These efficient high-dimensional simulation acquisitions are combined with exponentiated loss-likelihoods to provide a misspecification-robust characterisation of the marginal posterior distribution for all model parameters. The method successfully performs computationally efficient inference in a 100-dimensional space on canonical examples and compares favourably to existing Copula-ABC methods. We further illustrate the potential of this approach by fitting a bacterial transmission dynamics model to daycare centre data, which provides biologically coherent results on the strain competition in a 30-dimensional parameter space.

Diagnosing model misspecification and performing generalized Bayes' updates via probabilistic classifiers

Model misspecification is a long-standing enigma of the Bayesian inference framework as posteriors tend to get overly concentrated on ill-informed parameter values towards the large sample limit. Tempering of the likelihood has been established as a safer way to do updates from prior to posterior in the presence of model misspecification. At one extreme tempering can ignore the data altogether and at the other extreme it provides the standard Bayes' update when no misspecification is assumed to be present. However, it is an open issue how to best recognize misspecification and choose a suitable level of tempering without access to the true generating model. Here we show how probabilistic classifiers can be employed to resolve this issue. By training a probabilistic classifier to discriminate between simulated and observed data provides an estimate of the ratio between the model likelihood and the likelihood of the data under the unobserved true generative process, within the discriminatory abilities of the classifier. The expectation of the logarithm of a ratio with respect to the data generating process gives an estimation of the negative Kullback-Leibler divergence between the statistical generative model and the true generative distribution. Using a set of canonical examples we show that this divergence provides a useful misspecification diagnostic, a model comparison tool, and a method to inform a generalised Bayesian update in the presence of misspecification for likelihood-based models.

Learning pairwise Markov network structures using correlation neighborhoods

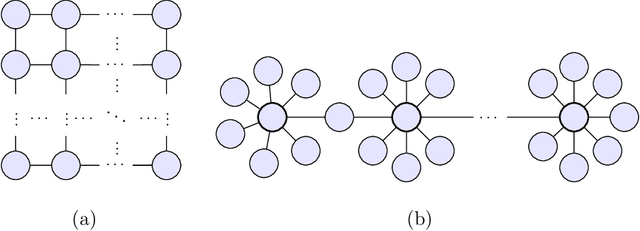
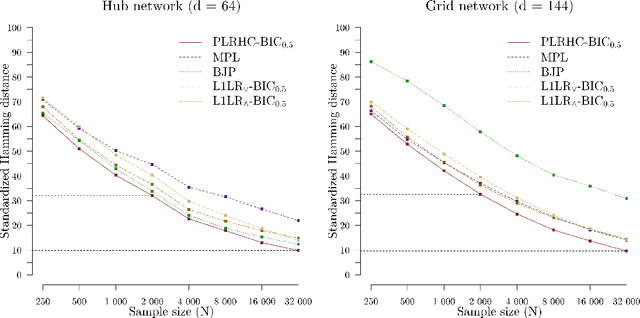
Markov networks are widely studied and used throughout multivariate statistics and computer science. In particular, the problem of learning the structure of Markov networks from data without invoking chordality assumptions in order to retain expressiveness of the model class has been given a considerable attention in the recent literature, where numerous constraint-based or score-based methods have been introduced. Here we develop a new search algorithm for the network score-optimization that has several computational advantages and scales well to high-dimensional data sets. The key observation behind the algorithm is that the neighborhood of a variable can be efficiently captured using local penalized likelihood ratio (PLR) tests by exploiting an exponential decay of correlations across the neighborhood with an increasing graph-theoretic distance from the focus node. The candidate neighborhoods are then processed by a two-stage hill-climbing (HC) algorithm. Our approach, termed fully as PLRHC-BIC$_{0.5}$, compares favorably against the state-of-the-art methods in all our experiments spanning both low- and high-dimensional networks and a wide range of sample sizes. An efficient implementation of PLRHC-BIC$_{0.5}$ is freely available from the URL: https://github.com/jurikuronen/plrhc.