Structure Learning of Contextual Markov Networks using Marginal Pseudo-likelihood

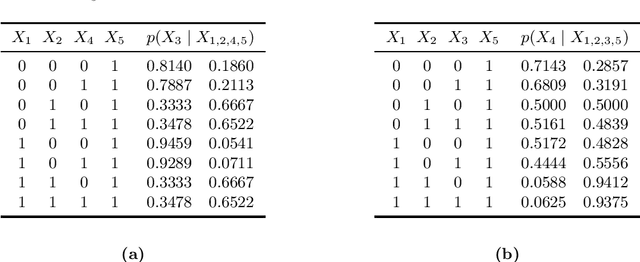
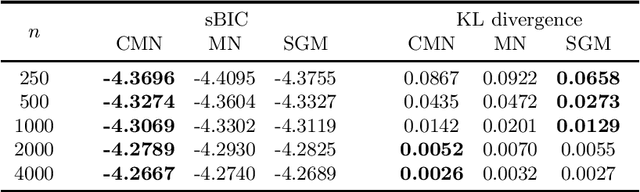
Markov networks are popular models for discrete multivariate systems where the dependence structure of the variables is specified by an undirected graph. To allow for more expressive dependence structures, several generalizations of Markov networks have been proposed. Here we consider the class of contextual Markov networks which takes into account possible context-specific independences among pairs of variables. Structure learning of contextual Markov networks is very challenging due to the extremely large number of possible structures. One of the main challenges has been to design a score, by which a structure can be assessed in terms of model fit related to complexity, without assuming chordality. Here we introduce the marginal pseudo-likelihood as an analytically tractable criterion for general contextual Markov networks. Our criterion is shown to yield a consistent structure estimator. Experiments demonstrate the favorable properties of our method in terms of predictive accuracy of the inferred models.

Marginal Pseudo-Likelihood Learning of Markov Network structures

Undirected graphical models known as Markov networks are popular for a wide variety of applications ranging from statistical physics to computational biology. Traditionally, learning of the network structure has been done under the assumption of chordality which ensures that efficient scoring methods can be used. In general, non-chordal graphs have intractable normalizing constants which renders the calculation of Bayesian and other scores difficult beyond very small-scale systems. Recently, there has been a surge of interest towards the use of regularized pseudo-likelihood methods for structural learning of large-scale Markov network models, as such an approach avoids the assumption of chordality. The currently available methods typically necessitate the use of a tuning parameter to adapt the level of regularization for a particular dataset, which can be optimized for example by cross-validation. Here we introduce a Bayesian version of pseudo-likelihood scoring of Markov networks, which enables an automatic regularization through marginalization over the nuisance parameters in the model. We prove consistency of the resulting MPL estimator for the network structure via comparison with the pseudo information criterion. Identification of the MPL-optimal network on a prescanned graph space is considered with both greedy hill climbing and exact pseudo-Boolean optimization algorithms. We find that for reasonable sample sizes the hill climbing approach most often identifies networks that are at a negligible distance from the restricted global optimum. Using synthetic and existing benchmark networks, the marginal pseudo-likelihood method is shown to generally perform favorably against recent popular inference methods for Markov networks.

Context-specific independence in graphical log-linear models

Log-linear models are the popular workhorses of analyzing contingency tables. A log-linear parameterization of an interaction model can be more expressive than a direct parameterization based on probabilities, leading to a powerful way of defining restrictions derived from marginal, conditional and context-specific independence. However, parameter estimation is often simpler under a direct parameterization, provided that the model enjoys certain decomposability properties. Here we introduce a cyclical projection algorithm for obtaining maximum likelihood estimates of log-linear parameters under an arbitrary context-specific graphical log-linear model, which needs not satisfy criteria of decomposability. We illustrate that lifting the restriction of decomposability makes the models more expressive, such that additional context-specific independencies embedded in real data can be identified. It is also shown how a context-specific graphical model can correspond to a non-hierarchical log-linear parameterization with a concise interpretation. This observation can pave way to further development of non-hierarchical log-linear models, which have been largely neglected due to their believed lack of interpretability.

Marginal and simultaneous predictive classification using stratified graphical models

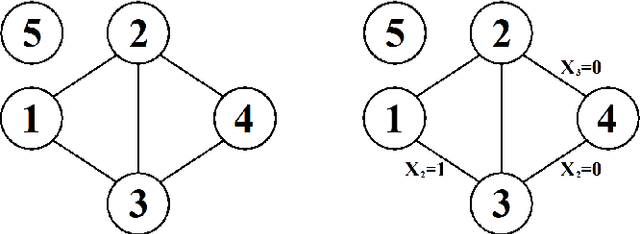
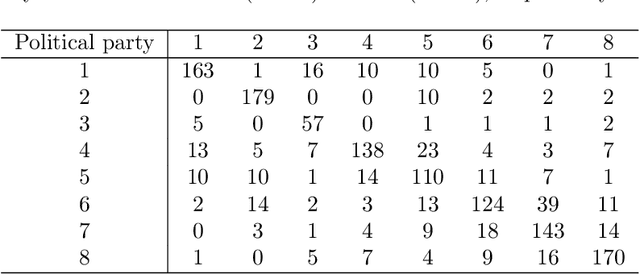
An inductive probabilistic classification rule must generally obey the principles of Bayesian predictive inference, such that all observed and unobserved stochastic quantities are jointly modeled and the parameter uncertainty is fully acknowledged through the posterior predictive distribution. Several such rules have been recently considered and their asymptotic behavior has been characterized under the assumption that the observed features or variables used for building a classifier are conditionally independent given a simultaneous labeling of both the training samples and those from an unknown origin. Here we extend the theoretical results to predictive classifiers acknowledging feature dependencies either through graphical models or sparser alternatives defined as stratified graphical models. We also show through experimentation with both synthetic and real data that the predictive classifiers based on stratified graphical models have consistently best accuracy compared with the predictive classifiers based on either conditionally independent features or on ordinary graphical models.

Stratified Graphical Models - Context-Specific Independence in Graphical Models

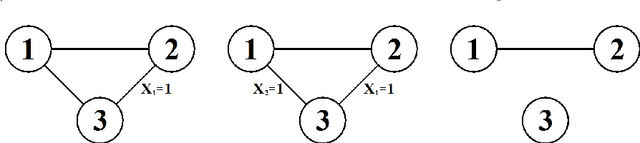
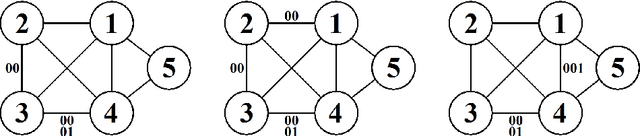
Theory of graphical models has matured over more than three decades to provide the backbone for several classes of models that are used in a myriad of applications such as genetic mapping of diseases, credit risk evaluation, reliability and computer security, etc. Despite of their generic applicability and wide adoptance, the constraints imposed by undirected graphical models and Bayesian networks have also been recognized to be unnecessarily stringent under certain circumstances. This observation has led to the proposal of several generalizations that aim at more relaxed constraints by which the models can impose local or context-specific dependence structures. Here we consider an additional class of such models, termed as stratified graphical models. We develop a method for Bayesian learning of these models by deriving an analytical expression for the marginal likelihood of data under a specific subclass of decomposable stratified models. A non-reversible Markov chain Monte Carlo approach is further used to identify models that are highly supported by the posterior distribution over the model space. Our method is illustrated and compared with ordinary graphical models through application to several real and synthetic datasets.

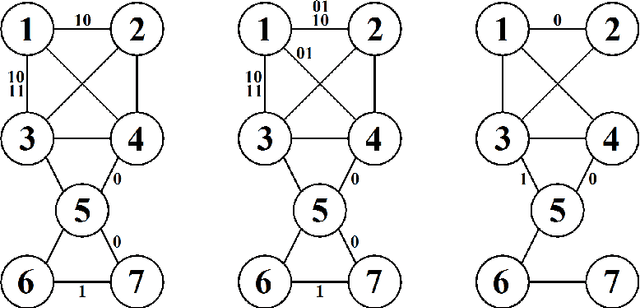
Labeled Directed Acyclic Graphs: a generalization of context-specific independence in directed graphical models

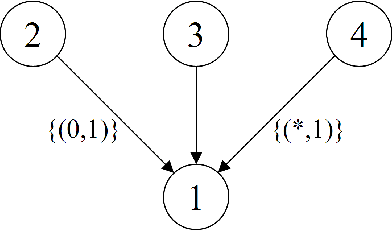
We introduce a novel class of labeled directed acyclic graph (LDAG) models for finite sets of discrete variables. LDAGs generalize earlier proposals for allowing local structures in the conditional probability distribution of a node, such that unrestricted label sets determine which edges can be deleted from the underlying directed acyclic graph (DAG) for a given context. Several properties of these models are derived, including a generalization of the concept of Markov equivalence classes. Efficient Bayesian learning of LDAGs is enabled by introducing an LDAG-based factorization of the Dirichlet prior for the model parameters, such that the marginal likelihood can be calculated analytically. In addition, we develop a novel prior distribution for the model structures that can appropriately penalize a model for its labeling complexity. A non-reversible Markov chain Monte Carlo algorithm combined with a greedy hill climbing approach is used for illustrating the useful properties of LDAG models for both real and synthetic data sets.

Learning Chordal Markov Networks by Constraint Satisfaction

We investigate the problem of learning the structure of a Markov network from data. It is shown that the structure of such networks can be described in terms of constraints which enables the use of existing solver technology with optimization capabilities to compute optimal networks starting from initial scores computed from the data. To achieve efficient encodings, we develop a novel characterization of Markov network structure using a balancing condition on the separators between cliques forming the network. The resulting translations into propositional satisfiability and its extensions such as maximum satisfiability, satisfiability modulo theories, and answer set programming, enable us to prove optimal certain network structures which have been previously found by stochastic search.