Structure Learning of Contextual Markov Networks using Marginal Pseudo-likelihood
Paper and Code
Mar 29, 2021
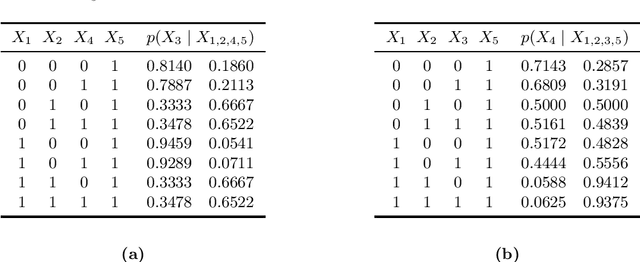

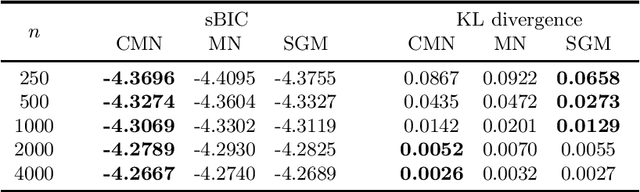
Markov networks are popular models for discrete multivariate systems where the dependence structure of the variables is specified by an undirected graph. To allow for more expressive dependence structures, several generalizations of Markov networks have been proposed. Here we consider the class of contextual Markov networks which takes into account possible context-specific independences among pairs of variables. Structure learning of contextual Markov networks is very challenging due to the extremely large number of possible structures. One of the main challenges has been to design a score, by which a structure can be assessed in terms of model fit related to complexity, without assuming chordality. Here we introduce the marginal pseudo-likelihood as an analytically tractable criterion for general contextual Markov networks. Our criterion is shown to yield a consistent structure estimator. Experiments demonstrate the favorable properties of our method in terms of predictive accuracy of the inferred models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge