Johan Pensar
Uncertainty quantification in automated valuation models with locally weighted conformal prediction
Dec 11, 2023



Abstract:Non-parametric machine learning models, such as random forests and gradient boosted trees, are frequently used to estimate house prices due to their predictive accuracy, but such methods are often limited in their ability to quantify prediction uncertainty. Conformal Prediction (CP) is a model-agnostic framework for constructing confidence sets around machine learning prediction models with minimal assumptions. However, due to the spatial dependencies observed in house prices, direct application of CP leads to confidence sets that are not calibrated everywhere, i.e., too large of confidence sets in certain geographical regions and too small in others. We survey various approaches to adjust the CP confidence set to account for this and demonstrate their performance on a data set from the housing market in Oslo, Norway. Our findings indicate that calibrating the confidence sets on a \textit{locally weighted} version of the non-conformity scores makes the coverage more consistently calibrated in different geographical regions. We also perform a simulation study on synthetically generated sale prices to empirically explore the performance of CP on housing market data under idealized conditions with known data-generating mechanisms.
Improving generalization of machine learning-identified biomarkers with causal modeling: an investigation into immune receptor diagnostics
Apr 20, 2022



Abstract:Machine learning is increasingly used to discover diagnostic and prognostic biomarkers from high-dimensional molecular data. However, a variety of factors related to experimental design may affect the ability to learn generalizable and clinically applicable diagnostics. Here, we argue that a causal perspective improves the identification of these challenges, and formalizes their relation to the robustness and generalization of machine learning-based diagnostics. To make for a concrete discussion, we focus on a specific, recently established high-dimensional biomarker - adaptive immune receptor repertoires (AIRRs). We discuss how the main biological and experimental factors of the AIRR domain may influence the learned biomarkers and provide easily adjustable simulations of such effects. In conclusion, we find that causal modeling improves machine learning-based biomarker robustness by identifying stable relations between variables and by guiding the adjustment of the relations and variables that vary between populations.
Structure Learning of Contextual Markov Networks using Marginal Pseudo-likelihood
Mar 29, 2021
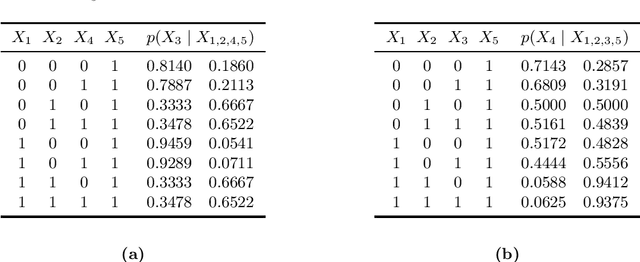

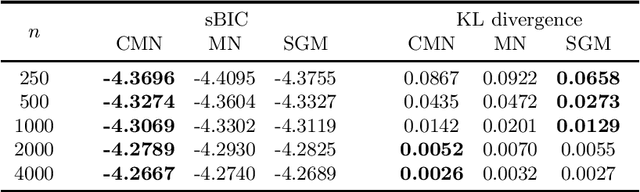
Abstract:Markov networks are popular models for discrete multivariate systems where the dependence structure of the variables is specified by an undirected graph. To allow for more expressive dependence structures, several generalizations of Markov networks have been proposed. Here we consider the class of contextual Markov networks which takes into account possible context-specific independences among pairs of variables. Structure learning of contextual Markov networks is very challenging due to the extremely large number of possible structures. One of the main challenges has been to design a score, by which a structure can be assessed in terms of model fit related to complexity, without assuming chordality. Here we introduce the marginal pseudo-likelihood as an analytically tractable criterion for general contextual Markov networks. Our criterion is shown to yield a consistent structure estimator. Experiments demonstrate the favorable properties of our method in terms of predictive accuracy of the inferred models.
Towards Scalable Bayesian Learning of Causal DAGs
Sep 30, 2020


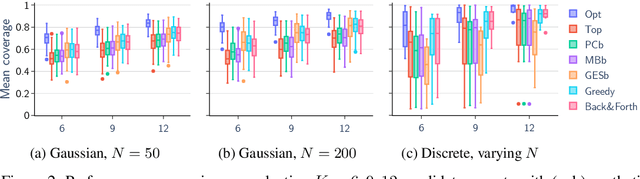
Abstract:We give methods for Bayesian inference of directed acyclic graphs, DAGs, and the induced causal effects from passively observed complete data. Our methods build on a recent Markov chain Monte Carlo scheme for learning Bayesian networks, which enables efficient approximate sampling from the graph posterior, provided that each node is assigned a small number K of candidate parents. We present algorithmic tricks to significantly reduce the space and time requirements of the method, making it feasible to use substantially larger values of K. Furthermore, we investigate the problem of selecting the candidate parents per node so as to maximize the covered posterior mass. Finally, we combine our sampling method with a novel Bayesian approach for estimating causal effects in linear Gaussian DAG models. Numerical experiments demonstrate the performance of our methods in detecting ancestor-descendant relations, and in effect estimation our Bayesian method is shown to outperform existing approaches.
Learning pairwise Markov network structures using correlation neighborhoods
Oct 30, 2019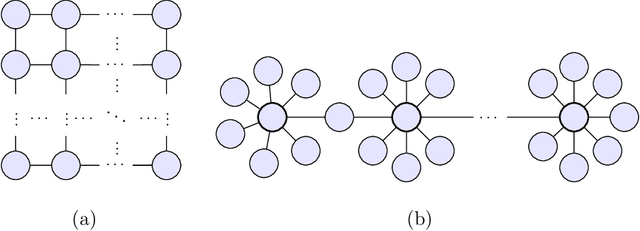


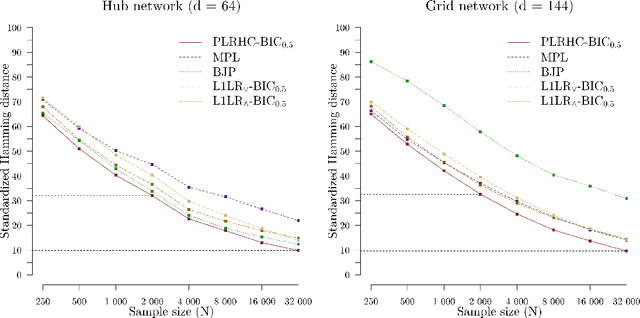
Abstract:Markov networks are widely studied and used throughout multivariate statistics and computer science. In particular, the problem of learning the structure of Markov networks from data without invoking chordality assumptions in order to retain expressiveness of the model class has been given a considerable attention in the recent literature, where numerous constraint-based or score-based methods have been introduced. Here we develop a new search algorithm for the network score-optimization that has several computational advantages and scales well to high-dimensional data sets. The key observation behind the algorithm is that the neighborhood of a variable can be efficiently captured using local penalized likelihood ratio (PLR) tests by exploiting an exponential decay of correlations across the neighborhood with an increasing graph-theoretic distance from the focus node. The candidate neighborhoods are then processed by a two-stage hill-climbing (HC) algorithm. Our approach, termed fully as PLRHC-BIC$_{0.5}$, compares favorably against the state-of-the-art methods in all our experiments spanning both low- and high-dimensional networks and a wide range of sample sizes. An efficient implementation of PLRHC-BIC$_{0.5}$ is freely available from the URL: https://github.com/jurikuronen/plrhc.
High-dimensional structure learning of binary pairwise Markov networks: A comparative numerical study
Jan 14, 2019



Abstract:Learning the undirected graph structure of a Markov network from data is a problem that has received a lot of attention during the last few decades. As a result of the general applicability of the model class, a myriad of methods have been developed in parallel in several research fields. Recently, as the size of the considered systems has increased, the focus of new methods has been shifted towards the high-dimensional domain. In particular, the introduction of the pseudo-likelihood function has pushed the limits of score-based methods originally based on the likelihood. At the same time, an array of methods based on simple pairwise tests have been developed to meet the challenges set by the increasingly large data sets in computational biology. Apart from being applicable on high-dimensional problems, methods based on the pseudo-likelihood and pairwise tests are fundamentally very different. In this work, we perform an extensive numerical study comparing the different types of methods on data generated by binary pairwise Markov networks. For sampling large networks, we use a parallelizable Gibbs sampler based on sparse restricted Boltzmann machines. Our results show that pairwise methods can be more accurate than pseudo-likelihood methods in settings often encountered in high-dimensional structure learning.
Learning Gaussian Graphical Models With Fractional Marginal Pseudo-likelihood
Feb 25, 2016



Abstract:We propose a Bayesian approximate inference method for learning the dependence structure of a Gaussian graphical model. Using pseudo-likelihood, we derive an analytical expression to approximate the marginal likelihood for an arbitrary graph structure without invoking any assumptions about decomposability. The majority of the existing methods for learning Gaussian graphical models are either restricted to decomposable graphs or require specification of a tuning parameter that may have a substantial impact on learned structures. By combining a simple sparsity inducing prior for the graph structures with a default reference prior for the model parameters, we obtain a fast and easily applicable scoring function that works well for even high-dimensional data. We demonstrate the favourable performance of our approach by large-scale comparisons against the leading methods for learning non-decomposable Gaussian graphical models. A theoretical justification for our method is provided by showing that it yields a consistent estimator of the graph structure.
Marginal Pseudo-Likelihood Learning of Markov Network structures
Nov 11, 2014



Abstract:Undirected graphical models known as Markov networks are popular for a wide variety of applications ranging from statistical physics to computational biology. Traditionally, learning of the network structure has been done under the assumption of chordality which ensures that efficient scoring methods can be used. In general, non-chordal graphs have intractable normalizing constants which renders the calculation of Bayesian and other scores difficult beyond very small-scale systems. Recently, there has been a surge of interest towards the use of regularized pseudo-likelihood methods for structural learning of large-scale Markov network models, as such an approach avoids the assumption of chordality. The currently available methods typically necessitate the use of a tuning parameter to adapt the level of regularization for a particular dataset, which can be optimized for example by cross-validation. Here we introduce a Bayesian version of pseudo-likelihood scoring of Markov networks, which enables an automatic regularization through marginalization over the nuisance parameters in the model. We prove consistency of the resulting MPL estimator for the network structure via comparison with the pseudo information criterion. Identification of the MPL-optimal network on a prescanned graph space is considered with both greedy hill climbing and exact pseudo-Boolean optimization algorithms. We find that for reasonable sample sizes the hill climbing approach most often identifies networks that are at a negligible distance from the restricted global optimum. Using synthetic and existing benchmark networks, the marginal pseudo-likelihood method is shown to generally perform favorably against recent popular inference methods for Markov networks.
Context-specific independence in graphical log-linear models
Sep 09, 2014



Abstract:Log-linear models are the popular workhorses of analyzing contingency tables. A log-linear parameterization of an interaction model can be more expressive than a direct parameterization based on probabilities, leading to a powerful way of defining restrictions derived from marginal, conditional and context-specific independence. However, parameter estimation is often simpler under a direct parameterization, provided that the model enjoys certain decomposability properties. Here we introduce a cyclical projection algorithm for obtaining maximum likelihood estimates of log-linear parameters under an arbitrary context-specific graphical log-linear model, which needs not satisfy criteria of decomposability. We illustrate that lifting the restriction of decomposability makes the models more expressive, such that additional context-specific independencies embedded in real data can be identified. It is also shown how a context-specific graphical model can correspond to a non-hierarchical log-linear parameterization with a concise interpretation. This observation can pave way to further development of non-hierarchical log-linear models, which have been largely neglected due to their believed lack of interpretability.
Marginal and simultaneous predictive classification using stratified graphical models
Jan 31, 2014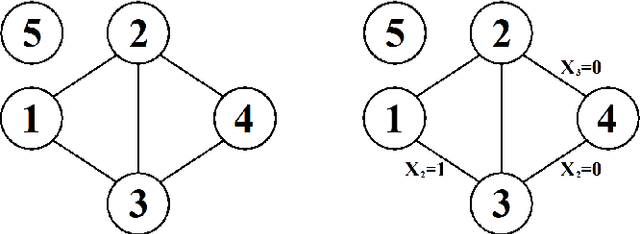


Abstract:An inductive probabilistic classification rule must generally obey the principles of Bayesian predictive inference, such that all observed and unobserved stochastic quantities are jointly modeled and the parameter uncertainty is fully acknowledged through the posterior predictive distribution. Several such rules have been recently considered and their asymptotic behavior has been characterized under the assumption that the observed features or variables used for building a classifier are conditionally independent given a simultaneous labeling of both the training samples and those from an unknown origin. Here we extend the theoretical results to predictive classifiers acknowledging feature dependencies either through graphical models or sparser alternatives defined as stratified graphical models. We also show through experimentation with both synthetic and real data that the predictive classifiers based on stratified graphical models have consistently best accuracy compared with the predictive classifiers based on either conditionally independent features or on ordinary graphical models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge