Learning pairwise Markov network structures using correlation neighborhoods
Paper and Code
Oct 30, 2019


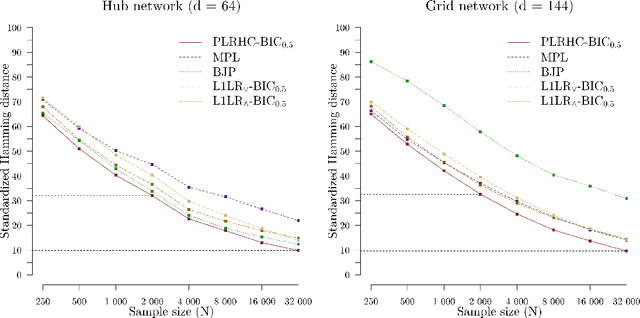
Markov networks are widely studied and used throughout multivariate statistics and computer science. In particular, the problem of learning the structure of Markov networks from data without invoking chordality assumptions in order to retain expressiveness of the model class has been given a considerable attention in the recent literature, where numerous constraint-based or score-based methods have been introduced. Here we develop a new search algorithm for the network score-optimization that has several computational advantages and scales well to high-dimensional data sets. The key observation behind the algorithm is that the neighborhood of a variable can be efficiently captured using local penalized likelihood ratio (PLR) tests by exploiting an exponential decay of correlations across the neighborhood with an increasing graph-theoretic distance from the focus node. The candidate neighborhoods are then processed by a two-stage hill-climbing (HC) algorithm. Our approach, termed fully as PLRHC-BIC$_{0.5}$, compares favorably against the state-of-the-art methods in all our experiments spanning both low- and high-dimensional networks and a wide range of sample sizes. An efficient implementation of PLRHC-BIC$_{0.5}$ is freely available from the URL: https://github.com/jurikuronen/plrhc.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge