Towards Scalable Bayesian Learning of Causal DAGs

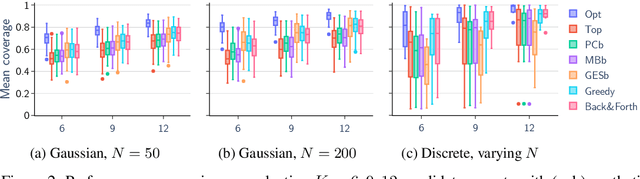
We give methods for Bayesian inference of directed acyclic graphs, DAGs, and the induced causal effects from passively observed complete data. Our methods build on a recent Markov chain Monte Carlo scheme for learning Bayesian networks, which enables efficient approximate sampling from the graph posterior, provided that each node is assigned a small number K of candidate parents. We present algorithmic tricks to significantly reduce the space and time requirements of the method, making it feasible to use substantially larger values of K. Furthermore, we investigate the problem of selecting the candidate parents per node so as to maximize the covered posterior mass. Finally, we combine our sampling method with a novel Bayesian approach for estimating causal effects in linear Gaussian DAG models. Numerical experiments demonstrate the performance of our methods in detecting ancestor-descendant relations, and in effect estimation our Bayesian method is shown to outperform existing approaches.

Treedy: A Heuristic for Counting and Sampling Subsets

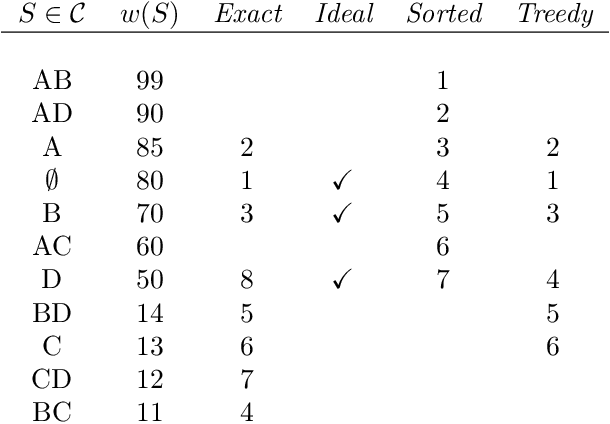
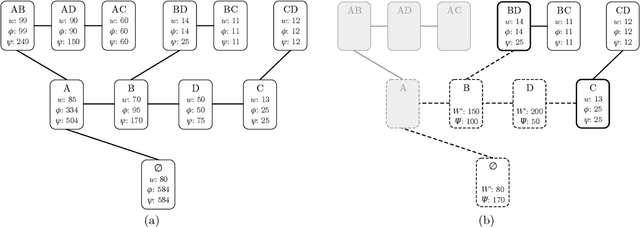
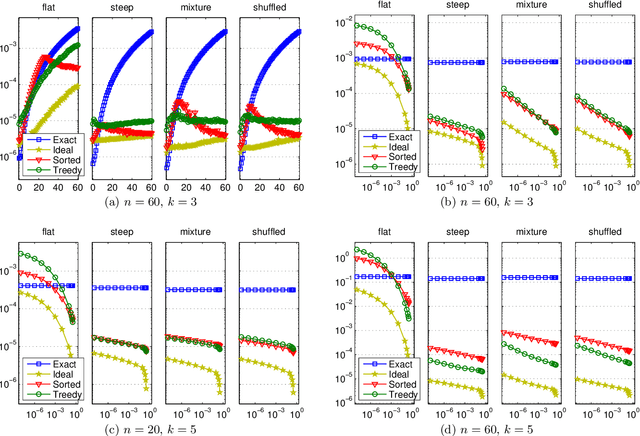
Consider a collection of weighted subsets of a ground set N. Given a query subset Q of N, how fast can one (1) find the weighted sum over all subsets of Q, and (2) sample a subset of Q proportionally to the weights? We present a tree-based greedy heuristic, Treedy, that for a given positive tolerance d answers such counting and sampling queries to within a guaranteed relative error d and total variation distance d, respectively. Experimental results on artificial instances and in application to Bayesian structure discovery in Bayesian networks show that approximations yield dramatic savings in running time compared to exact computation, and that Treedy typically outperforms a previously proposed sorting-based heuristic.

On Finding Optimal Polytrees

Inferring probabilistic networks from data is a notoriously difficult task. Under various goodness-of-fit measures, finding an optimal network is NP-hard, even if restricted to polytrees of bounded in-degree. Polynomial-time algorithms are known only for rare special cases, perhaps most notably for branchings, that is, polytrees in which the in-degree of every node is at most one. Here, we study the complexity of finding an optimal polytree that can be turned into a branching by deleting some number of arcs or nodes, treated as a parameter. We show that the problem can be solved via a matroid intersection formulation in polynomial time if the number of deleted arcs is bounded by a constant. The order of the polynomial time bound depends on this constant, hence the algorithm does not establish fixed-parameter tractability when parameterized by the number of deleted arcs. We show that a restricted version of the problem allows fixed-parameter tractability and hence scales well with the parameter. We contrast this positive result by showing that if we parameterize by the number of deleted nodes, a somewhat more powerful parameter, the problem is not fixed-parameter tractable, subject to a complexity-theoretic assumption.

Advances in exact Bayesian structure discovery in Bayesian networks

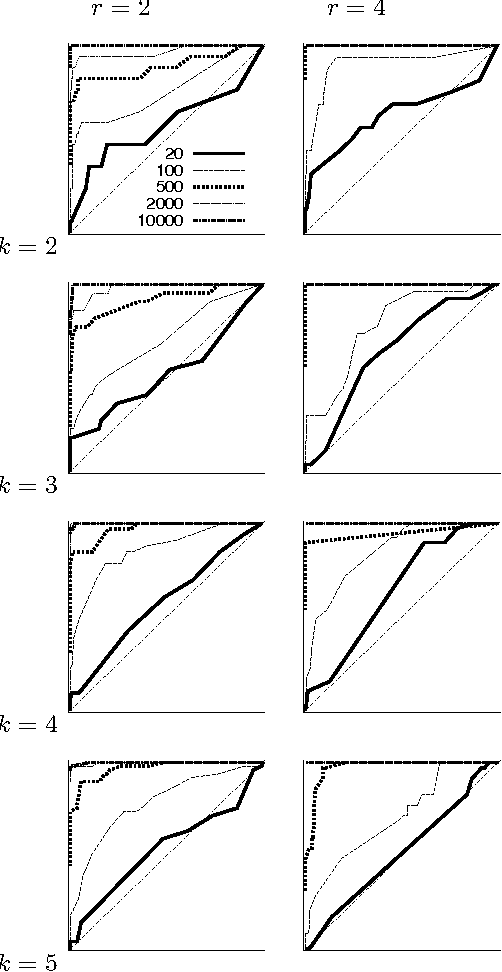
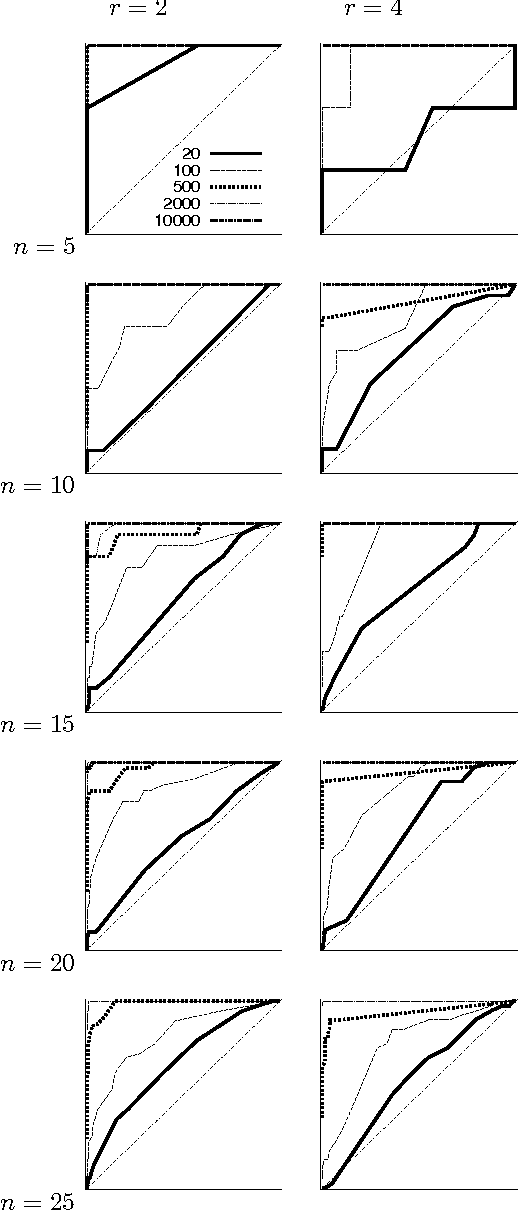
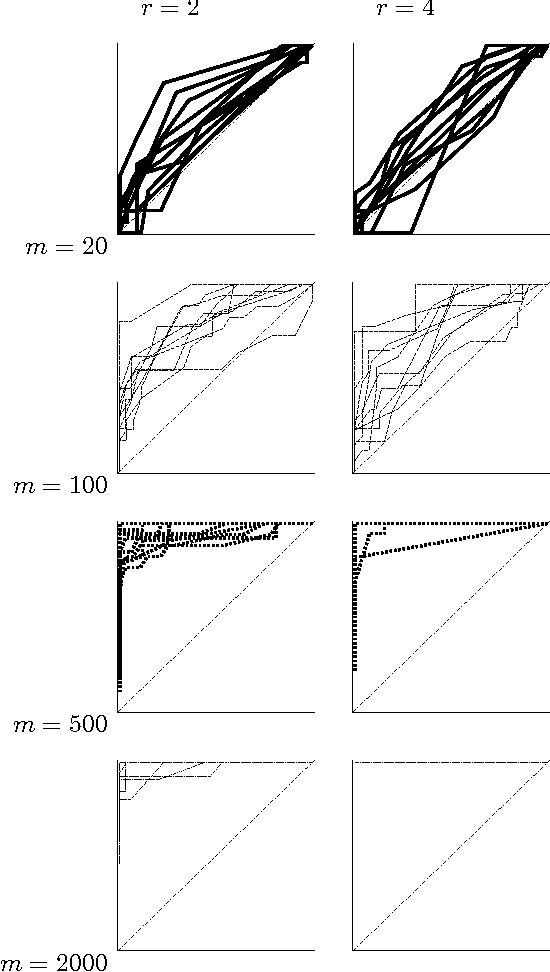
We consider a Bayesian method for learning the Bayesian network structure from complete data. Recently, Koivisto and Sood (2004) presented an algorithm that for any single edge computes its marginal posterior probability in O(n 2^n) time, where n is the number of attributes; the number of parents per attribute is bounded by a constant. In this paper we show that the posterior probabilities for all the n (n - 1) potential edges can be computed in O(n 2^n) total time. This result is achieved by a forward-backward technique and fast Moebius transform algorithms, which are of independent interest. The resulting speedup by a factor of about n^2 allows us to experimentally study the statistical power of learning moderate-size networks. We report results from a simulation study that covers data sets with 20 to 10,000 records over 5 to 25 discrete attributes

Exact Structure Discovery in Bayesian Networks with Less Space

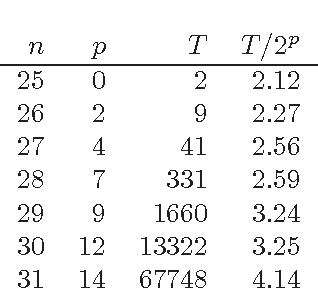
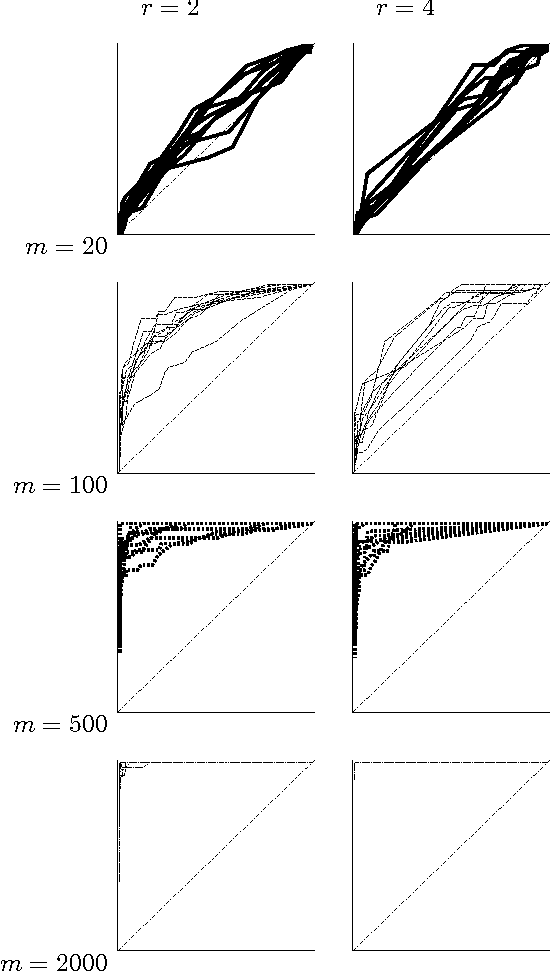
The fastest known exact algorithms for scorebased structure discovery in Bayesian networks on n nodes run in time and space 2nnO(1). The usage of these algorithms is limited to networks on at most around 25 nodes mainly due to the space requirement. Here, we study space-time tradeoffs for finding an optimal network structure. When little space is available, we apply the Gurevich-Shelah recurrence-originally proposed for the Hamiltonian path problem-and obtain time 22n-snO(1) in space 2snO(1) for any s = n/2, n/4, n/8, . . .; we assume the indegree of each node is bounded by a constant. For the more practical setting with moderate amounts of space, we present a novel scheme. It yields running time 2n(3/2)pnO(1) in space 2n(3/4)pnO(1) for any p = 0, 1, . . ., n/2; these bounds hold as long as the indegrees are at most 0.238n. Furthermore, the latter scheme allows easy and efficient parallelization beyond previous algorithms. We also explore empirically the potential of the presented techniques.

Partial Order MCMC for Structure Discovery in Bayesian Networks

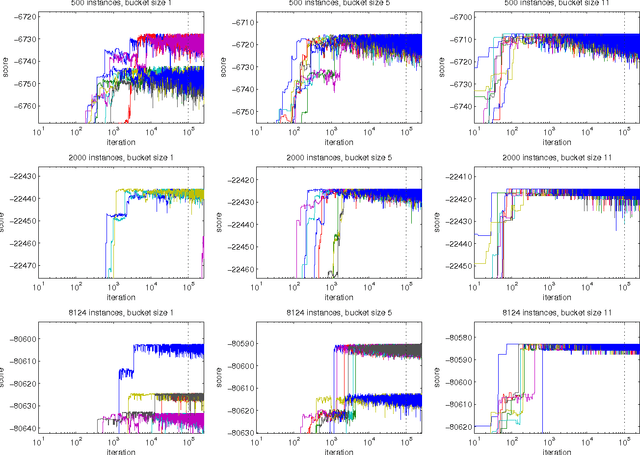
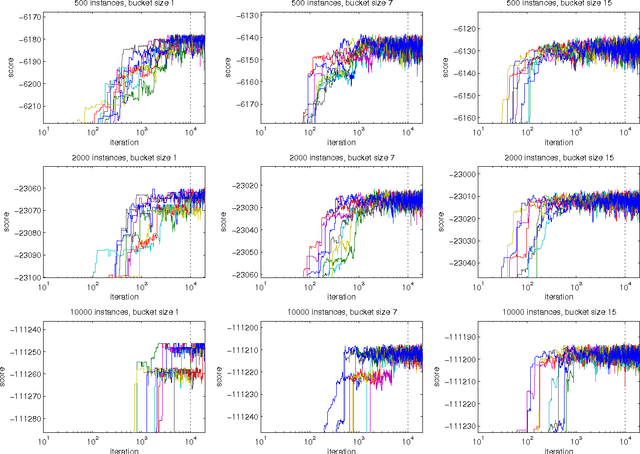
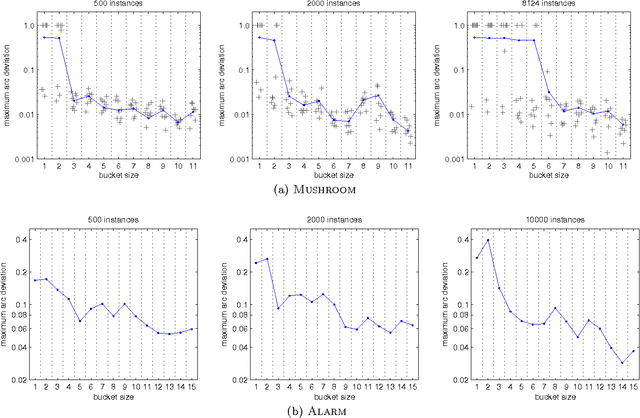
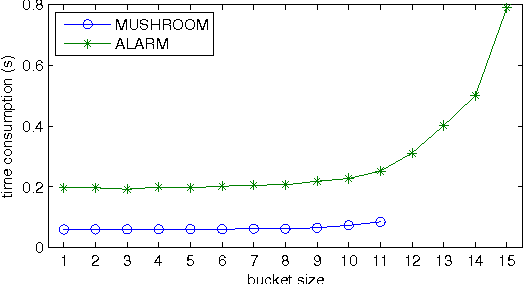
We present a new Markov chain Monte Carlo method for estimating posterior probabilities of structural features in Bayesian networks. The method draws samples from the posterior distribution of partial orders on the nodes; for each sampled partial order, the conditional probabilities of interest are computed exactly. We give both analytical and empirical results that suggest the superiority of the new method compared to previous methods, which sample either directed acyclic graphs or linear orders on the nodes.