Treedy: A Heuristic for Counting and Sampling Subsets

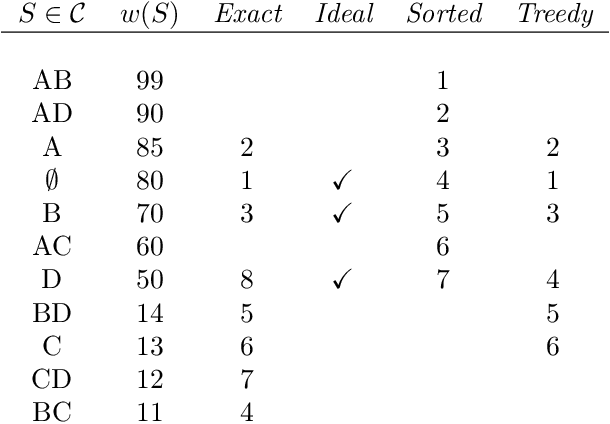
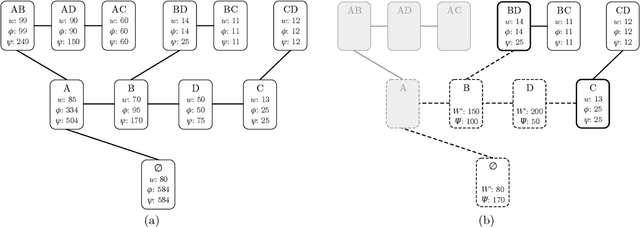
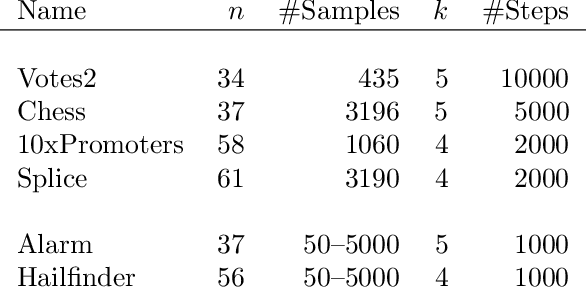
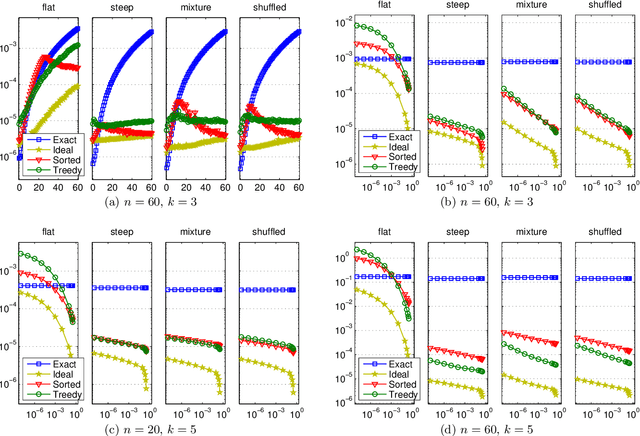
Consider a collection of weighted subsets of a ground set N. Given a query subset Q of N, how fast can one (1) find the weighted sum over all subsets of Q, and (2) sample a subset of Q proportionally to the weights? We present a tree-based greedy heuristic, Treedy, that for a given positive tolerance d answers such counting and sampling queries to within a guaranteed relative error d and total variation distance d, respectively. Experimental results on artificial instances and in application to Bayesian structure discovery in Bayesian networks show that approximations yield dramatic savings in running time compared to exact computation, and that Treedy typically outperforms a previously proposed sorting-based heuristic.

Local Structure Discovery in Bayesian Networks

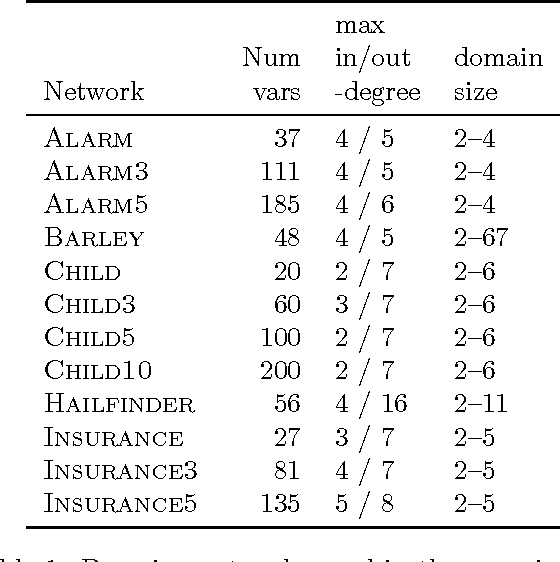
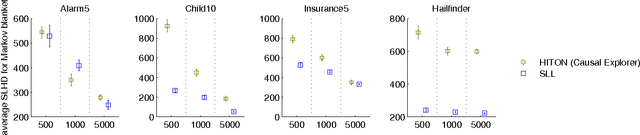
Learning a Bayesian network structure from data is an NP-hard problem and thus exact algorithms are feasible only for small data sets. Therefore, network structures for larger networks are usually learned with various heuristics. Another approach to scaling up the structure learning is local learning. In local learning, the modeler has one or more target variables that are of special interest; he wants to learn the structure near the target variables and is not interested in the rest of the variables. In this paper, we present a score-based local learning algorithm called SLL. We conjecture that our algorithm is theoretically sound in the sense that it is optimal in the limit of large sample size. Empirical results suggest that SLL is competitive when compared to the constraint-based HITON algorithm. We also study the prospects of constructing the network structure for the whole node set based on local results by presenting two algorithms and comparing them to several heuristics.

Partial Order MCMC for Structure Discovery in Bayesian Networks

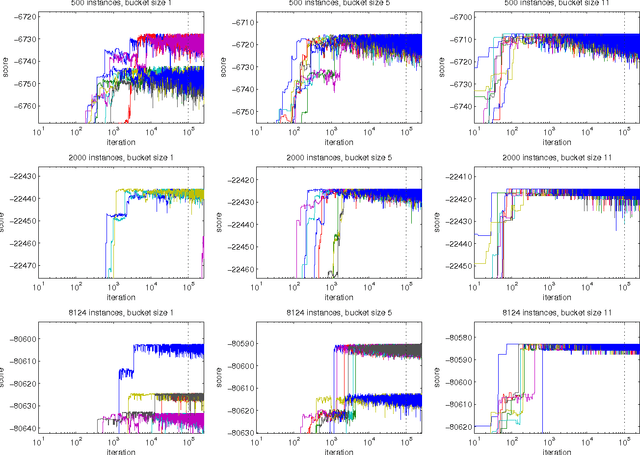
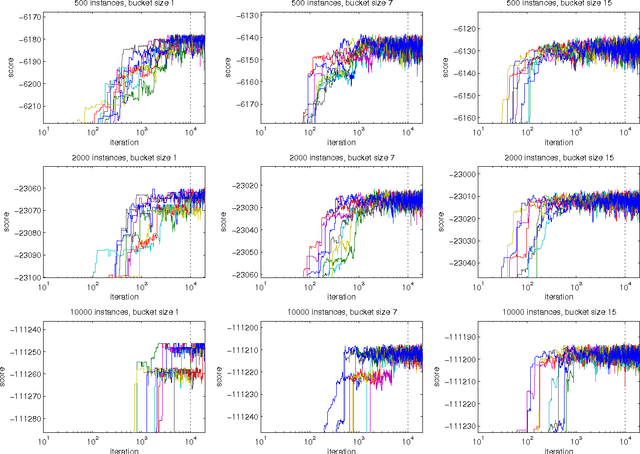
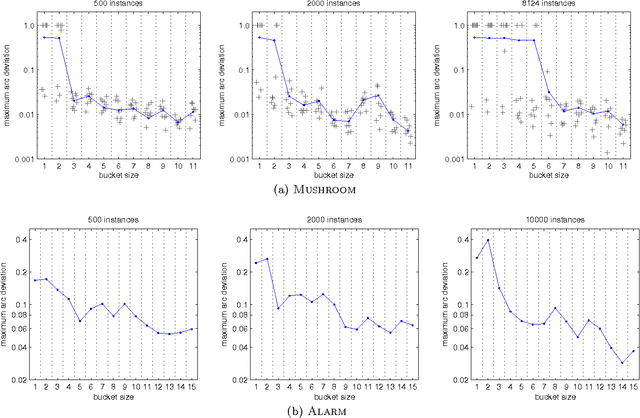
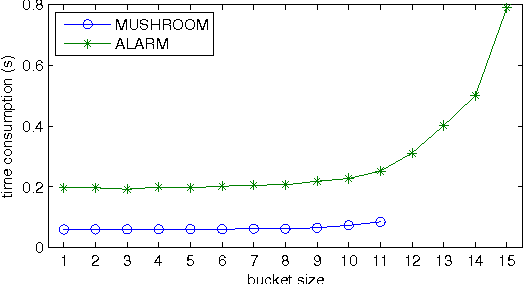
We present a new Markov chain Monte Carlo method for estimating posterior probabilities of structural features in Bayesian networks. The method draws samples from the posterior distribution of partial orders on the nodes; for each sampled partial order, the conditional probabilities of interest are computed exactly. We give both analytical and empirical results that suggest the superiority of the new method compared to previous methods, which sample either directed acyclic graphs or linear orders on the nodes.