Structural perspective on constraint-based learning of Markov networks

Markov networks are probabilistic graphical models that employ undirected graphs to depict conditional independence relationships among variables. Our focus lies in constraint-based structure learning, which entails learning the undirected graph from data through the execution of conditional independence tests. We establish theoretical limits concerning two critical aspects of constraint-based learning of Markov networks: the number of tests and the sizes of the conditioning sets. These bounds uncover an exciting interplay between the structural properties of the graph and the amount of tests required to learn a Markov network. The starting point of our work is that the graph parameter maximum pairwise connectivity, $\kappa$, that is, the maximum number of vertex-disjoint paths connecting a pair of vertices in the graph, is responsible for the sizes of independence tests required to learn the graph. On one hand, we show that at least one test with the size of the conditioning set at least $\kappa$ is always necessary. On the other hand, we prove that any graph can be learned by performing tests of size at most $\kappa$. This completely resolves the question of the minimum size of conditioning sets required to learn the graph. When it comes to the number of tests, our upper bound on the sizes of conditioning sets implies that every $n$-vertex graph can be learned by at most $n^{\kappa}$ tests with conditioning sets of sizes at most $\kappa$. We show that for any upper bound $q$ on the sizes of the conditioning sets, there exist graphs with $O(n q)$ vertices that require at least $n^{\Omega(\kappa)}$ tests to learn. This lower bound holds even when the treewidth and the maximum degree of the graph are at most $\kappa+2$. On the positive side, we prove that every graph of bounded treewidth can be learned by a polynomial number of tests with conditioning sets of sizes at most $2\kappa$.

Inspecting class hierarchies in classification-based metric learning models

Most classification models treat all misclassifications equally. However, different classes may be related, and these hierarchical relationships must be considered in some classification problems. These problems can be addressed by using hierarchical information during training. Unfortunately, this information is not available for all datasets. Many classification-based metric learning methods use class representatives in embedding space to represent different classes. The relationships among the learned class representatives can then be used to estimate class hierarchical structures. If we have a predefined class hierarchy, the learned class representatives can be assessed to determine whether the metric learning model learned semantic distances that match our prior knowledge. In this work, we train a softmax classifier and three metric learning models with several training options on benchmark and real-world datasets. In addition to the standard classification accuracy, we evaluate the hierarchical inference performance by inspecting learned class representatives and the hierarchy-informed performance, i.e., the classification performance, and the metric learning performance by considering predefined hierarchical structures. Furthermore, we investigate how the considered measures are affected by various models and training options. When our proposed ProxyDR model is trained without using predefined hierarchical structures, the hierarchical inference performance is significantly better than that of the popular NormFace model. Additionally, our model enhances some hierarchy-informed performance measures under the same training options. We also found that convolutional neural networks (CNNs) with random weights correspond to the predefined hierarchies better than random chance.

Realistic mask generation for matter-wave lithography via machine learning

Fast production of large area patterns with nanometre resolution is crucial for the established semiconductor industry and for enabling industrial-scale production of next-generation quantum devices. Metastable atom lithography with binary holography masks has been suggested as a higher resolution/low-cost alternative to the current state of the art: extreme ultraviolet (EUV) lithography. However, it was recently shown that the interaction of the metastable atoms with the mask material (SiN) leads to a strong perturbation of the wavefront, not included in existing mask generation theory, which is based on classical scalar waves. This means that the inverse problem (creating a mask based on the desired pattern) cannot be solved analytically even in 1D. Here we present a machine learning approach to mask generation targeted for metastable atoms. Our algorithm uses a combination of genetic optimisation and deep learning to obtain the mask. A novel deep neural architecture is trained to produce an initial approximation of the mask. This approximation is then used to generate the initial population of the genetic optimisation algorithm that can converge to arbitrary precision. We demonstrate the generation of arbitrary 1D patterns for system dimensions within the Fraunhofer approximation limit.

Distance-Ratio-Based Formulation for Metric Learning

In metric learning, the goal is to learn an embedding so that data points with the same class are close to each other and data points with different classes are far apart. We propose a distance-ratio-based (DR) formulation for metric learning. Like softmax-based formulation for metric learning, it models $p(y=c|x')$, which is a probability that a query point $x'$ belongs to a class $c$. The DR formulation has two useful properties. First, the corresponding loss is not affected by scale changes of an embedding. Second, it outputs the optimal (maximum or minimum) classification confidence scores on representing points for classes. To demonstrate the effectiveness of our formulation, we conduct few-shot classification experiments using softmax-based and DR formulations on CUB and mini-ImageNet datasets. The results show that DR formulation generally enables faster and more stable metric learning than the softmax-based formulation. As a result, using DR formulation achieves improved or comparable generalization performances.

Learning Large DAGs by Combining Continuous Optimization and Feedback Arc Set Heuristics

Bayesian networks represent relations between variables using a directed acyclic graph (DAG). Learning the DAG is an NP-hard problem and exact learning algorithms are feasible only for small sets of variables. We propose two scalable heuristics for learning DAGs in the linear structural equation case. Our methods learn the DAG by alternating between unconstrained gradient descent-based step to optimize an objective function and solving a maximum acyclic subgraph problem to enforce acyclicity. Thanks to this decoupling, our methods scale up beyond thousands of variables.

Distributed Bayesian Matrix Factorization with Limited Communication

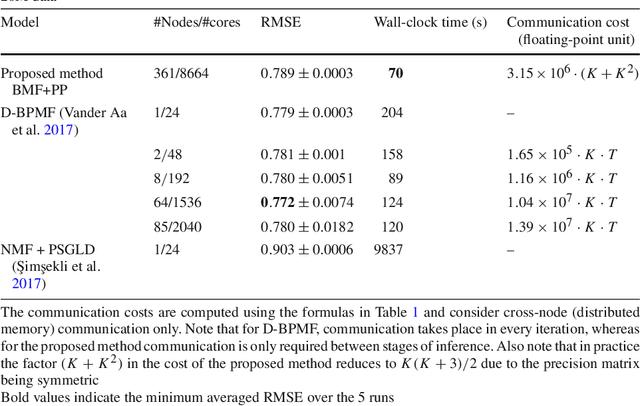
Bayesian matrix factorization (BMF) is a powerful tool for producing low-rank representations of matrices and for predicting missing values and their confidence intervals. Scaling up the posterior inference for massive-scale matrices is challenging and requires distributing both data and computation over many workers, making communication the main computational bottleneck. Embarrassingly parallel inference would remove the communication needed, by using completely independent computations on different data subsets, but suffers from the inherent unidentifiability of BMF solutions. We introduce a hierarchical decomposition of the joint posterior distribution, which couples the subset inferences, allowing for embarrassingly parallel computations in a sequence of at most three stages. Using an efficient approximate implementation, we show empirically on both real and simulated data that our distributed approach is able to achieve a speed-up of almost an order of magnitude, with a negligible effect on predictive accuracy.

Learning Structures of Bayesian Networks for Variable Groups

Bayesian networks, and especially their structures, are powerful tools for representing conditional independencies and dependencies between random variables. In applications where related variables form a priori known groups, chosen to represent different "views" to or aspects of the same entities, one may be more interested in modeling dependencies between groups of variables rather than between individual variables. Motivated by this, we study prospects of representing relationships between variable groups using Bayesian network structures. We show that for dependency structures between groups to be expressible exactly, the data have to satisfy the so-called groupwise faithfulness assumption. We also show that one cannot learn causal relations between groups using only groupwise conditional independencies, but also variable-wise relations are needed. Additionally, we present algorithms for finding the groupwise dependency structures.

Local Structure Discovery in Bayesian Networks

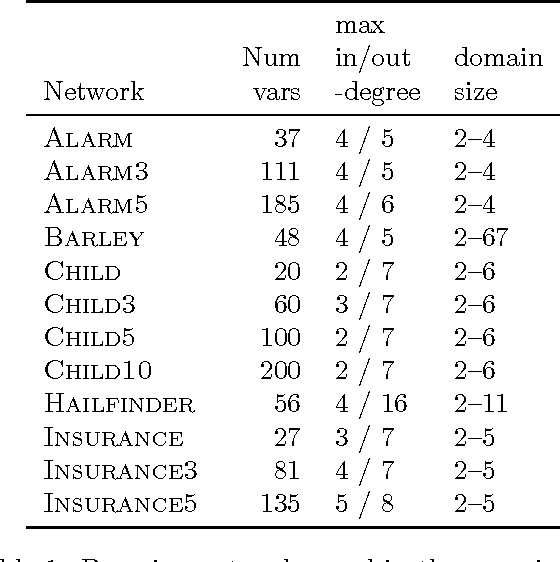
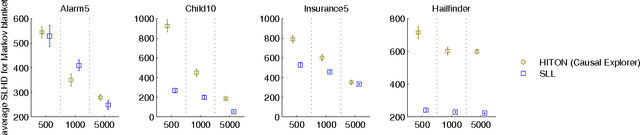
Learning a Bayesian network structure from data is an NP-hard problem and thus exact algorithms are feasible only for small data sets. Therefore, network structures for larger networks are usually learned with various heuristics. Another approach to scaling up the structure learning is local learning. In local learning, the modeler has one or more target variables that are of special interest; he wants to learn the structure near the target variables and is not interested in the rest of the variables. In this paper, we present a score-based local learning algorithm called SLL. We conjecture that our algorithm is theoretically sound in the sense that it is optimal in the limit of large sample size. Empirical results suggest that SLL is competitive when compared to the constraint-based HITON algorithm. We also study the prospects of constructing the network structure for the whole node set based on local results by presenting two algorithms and comparing them to several heuristics.

Exact Structure Discovery in Bayesian Networks with Less Space

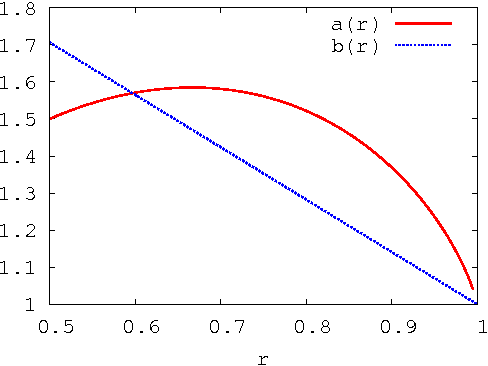
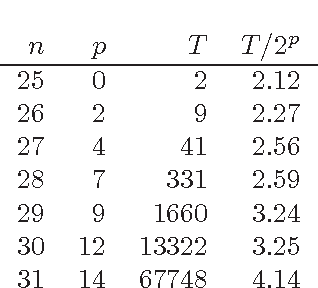
The fastest known exact algorithms for scorebased structure discovery in Bayesian networks on n nodes run in time and space 2nnO(1). The usage of these algorithms is limited to networks on at most around 25 nodes mainly due to the space requirement. Here, we study space-time tradeoffs for finding an optimal network structure. When little space is available, we apply the Gurevich-Shelah recurrence-originally proposed for the Hamiltonian path problem-and obtain time 22n-snO(1) in space 2snO(1) for any s = n/2, n/4, n/8, . . .; we assume the indegree of each node is bounded by a constant. For the more practical setting with moderate amounts of space, we present a novel scheme. It yields running time 2n(3/2)pnO(1) in space 2n(3/4)pnO(1) for any p = 0, 1, . . ., n/2; these bounds hold as long as the indegrees are at most 0.238n. Furthermore, the latter scheme allows easy and efficient parallelization beyond previous algorithms. We also explore empirically the potential of the presented techniques.

Partial Order MCMC for Structure Discovery in Bayesian Networks

We present a new Markov chain Monte Carlo method for estimating posterior probabilities of structural features in Bayesian networks. The method draws samples from the posterior distribution of partial orders on the nodes; for each sampled partial order, the conditional probabilities of interest are computed exactly. We give both analytical and empirical results that suggest the superiority of the new method compared to previous methods, which sample either directed acyclic graphs or linear orders on the nodes.