Variance reduction for distributed stochastic gradient MCMC

Stochastic gradient MCMC methods, such as stochastic gradient Langevin dynamics (SGLD), have emerged as one of the dominant approaches for posterior sampling in large-scale settings. While gradient evaluations based on only a small fraction of the data significantly reduce the computational cost, they may suffer from high variance, leading to slow convergence. In distributed settings, where the data lie scattered across a number of workers, the problem of high variance is particularly imminent and is even worse if the data subsets held by the workers are very heterogeneous. The impact of variance reduction has been studied in serial settings but not in distributed scenarios so far. In this work, we derive variance bounds for distributed SGLD and introduce the concept of conducive gradients, zero-mean stochastic gradients that serve as a mechanism for sharing probabilistic information between workers. We introduce a novel stochastic gradient estimator which incorporates the inducive gradients, and show both theoretically and empirically that it reduces variance, and hence improves convergence.

A High-Performance Implementation of Bayesian Matrix Factorization with Limited Communication

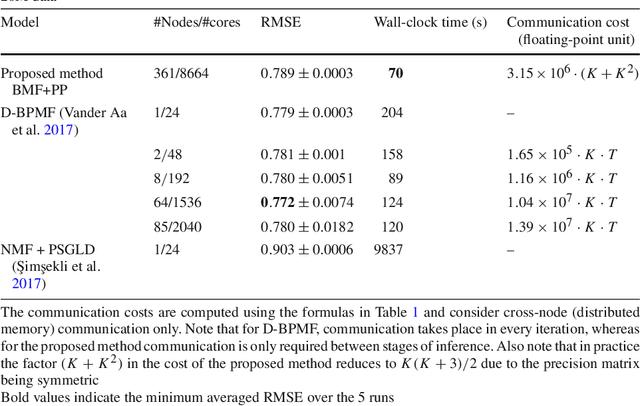
Matrix factorization is a very common machine learning technique in recommender systems. Bayesian Matrix Factorization (BMF) algorithms would be attractive because of their ability to quantify uncertainty in their predictions and avoid over-fitting, combined with high prediction accuracy. However, they have not been widely used on large-scale data because of their prohibitive computational cost. In recent work, efforts have been made to reduce the cost, both by improving the scalability of the BMF algorithm as well as its implementation, but so far mainly separately. In this paper we show that the state-of-the-art of both approaches to scalability can be combined. We combine the recent highly-scalable Posterior Propagation algorithm for BMF, which parallelizes computation of blocks of the matrix, with a distributed BMF implementation that users asynchronous communication within each block. We show that the combination of the two methods gives substantial improvements in the scalability of BMF on web-scale datasets, when the goal is to reduce the wall-clock time.

Scalable Bayesian Non-linear Matrix Completion

Matrix completion aims to predict missing elements in a partially observed data matrix which in typical applications, such as collaborative filtering, is large and extremely sparsely observed. A standard solution is matrix factorization, which predicts unobserved entries as linear combinations of latent variables. We generalize to non-linear combinations in massive-scale matrices. Bayesian approaches have been proven beneficial in linear matrix completion, but not applied in the more general non-linear case, due to limited scalability. We introduce a Bayesian non-linear matrix completion algorithm, which is based on a recent Bayesian formulation of Gaussian process latent variable models. To solve the challenges regarding scalability and computation, we propose a data-parallel distributed computational approach with a restricted communication scheme. We evaluate our method on challenging out-of-matrix prediction tasks using both simulated and real-world data.

Embarrassingly parallel MCMC using deep invertible transformations

While MCMC methods have become a main work-horse for Bayesian inference, scaling them to large distributed datasets is still a challenge. Embarrassingly parallel MCMC strategies take a divide-and-conquer stance to achieve this by writing the target posterior as a product of subposteriors, running MCMC for each of them in parallel and subsequently combining the results. The challenge then lies in devising efficient aggregation strategies. Current strategies trade-off between approximation quality, and costs of communication and computation. In this work, we introduce a novel method that addresses these issues simultaneously. Our key insight is to introduce a deep invertible transformation to approximate each of the subposteriors. These approximations can be made accurate even for complex distributions and serve as intermediate representations, keeping the total communication cost limited. Moreover, they enable us to sample from the product of the subposteriors using an efficient and stable importance sampling scheme. We demonstrate the approach outperforms available state-of-the-art methods in a range of challenging scenarios, including high-dimensional and heterogeneous subposteriors.

Expectation propagation as a way of life: A framework for Bayesian inference on partitioned data

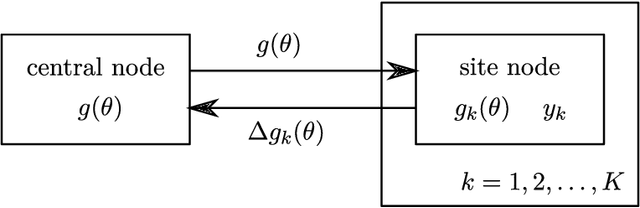
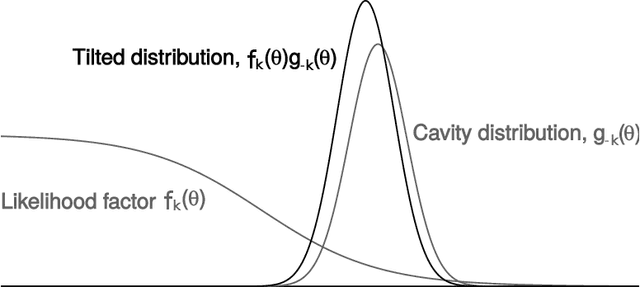
A common approach for Bayesian computation with big data is to partition the data into smaller pieces, perform local inference for each piece separately, and finally combine the results to obtain an approximation to the global posterior. Looking at this from the bottom up, one can perform separate analyses on individual sources of data and then combine these in a larger Bayesian model. In either case, the idea of distributed modeling and inference has both conceptual and computational appeal, but from the Bayesian perspective there is no general way of handling the prior distribution: if the prior is included in each separate inference, it will be multiply-counted when the inferences are combined; but if the prior is itself divided into pieces, it may not provide enough regularization for each separate computation, thus eliminating one of the key advantages of Bayesian methods. To resolve this dilemma, we propose expectation propagation (EP) as a general prototype for distributed Bayesian inference. The central idea is to factor the likelihood according to the data partitions, and to iteratively combine each factor with an approximate model of the prior and all other parts of the data, thus producing an overall approximation to the global posterior at convergence. In this paper, we give an introduction to EP and an overview of some recent developments of the method, with particular emphasis on its use in combining inferences from partitioned data. In addition to distributed modeling of large datasets, our unified treatment also includes hierarchical modeling of data with a naturally partitioned structure. The paper describes a general algorithmic framework, rather than a specific algorithm, and presents an example implementation for it.

Distributed Bayesian Matrix Factorization with Limited Communication

Bayesian matrix factorization (BMF) is a powerful tool for producing low-rank representations of matrices and for predicting missing values and their confidence intervals. Scaling up the posterior inference for massive-scale matrices is challenging and requires distributing both data and computation over many workers, making communication the main computational bottleneck. Embarrassingly parallel inference would remove the communication needed, by using completely independent computations on different data subsets, but suffers from the inherent unidentifiability of BMF solutions. We introduce a hierarchical decomposition of the joint posterior distribution, which couples the subset inferences, allowing for embarrassingly parallel computations in a sequence of at most three stages. Using an efficient approximate implementation, we show empirically on both real and simulated data that our distributed approach is able to achieve a speed-up of almost an order of magnitude, with a negligible effect on predictive accuracy.

Bayesian inference in hierarchical models by combining independent posteriors

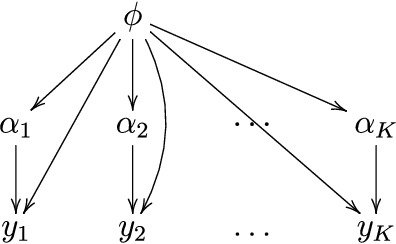
Hierarchical models are versatile tools for joint modeling of data sets arising from different, but related, sources. Fully Bayesian inference may, however, become computationally prohibitive if the source-specific data models are complex, or if the number of sources is very large. To facilitate computation, we propose an approach, where inference is first made independently for the parameters of each data set, whereupon the obtained posterior samples are used as observed data in a substitute hierarchical model, based on a scaled likelihood function. Compared to direct inference in a full hierarchical model, the approach has the advantage of being able to speed up convergence by breaking down the initial large inference problem into smaller individual subproblems with better convergence properties. Moreover it enables parallel processing of the possibly complex inferences of the source-specific parameters, which may otherwise create a computational bottleneck if processed jointly as part of a hierarchical model. The approach is illustrated with both simulated and real data.

Modelling-based experiment retrieval: A case study with gene expression clustering

Motivation: Public and private repositories of experimental data are growing to sizes that require dedicated methods for finding relevant data. To improve on the state of the art of keyword searches from annotations, methods for content-based retrieval have been proposed. In the context of gene expression experiments, most methods retrieve gene expression profiles, requiring each experiment to be expressed as a single profile, typically of case vs. control. A more general, recently suggested alternative is to retrieve experiments whose models are good for modelling the query dataset. However, for very noisy and high-dimensional query data, this retrieval criterion turns out to be very noisy as well. Results: We propose doing retrieval using a denoised model of the query dataset, instead of the original noisy dataset itself. To this end, we introduce a general probabilistic framework, where each experiment is modelled separately and the retrieval is done by finding related models. For retrieval of gene expression experiments, we use a probabilistic model called product partition model, which induces a clustering of genes that show similar expression patterns across a number of samples. The suggested metric for retrieval using clusterings is the normalized information distance. Empirical results finally suggest that inference for the full probabilistic model can be approximated with good performance using computationally faster heuristic clustering approaches (e.g. $k$-means). The method is highly scalable and straightforward to apply to construct a general-purpose gene expression experiment retrieval method. Availability: The method can be implemented using standard clustering algorithms and normalized information distance, available in many statistical software packages.