Distributed Bayesian Matrix Factorization with Limited Communication

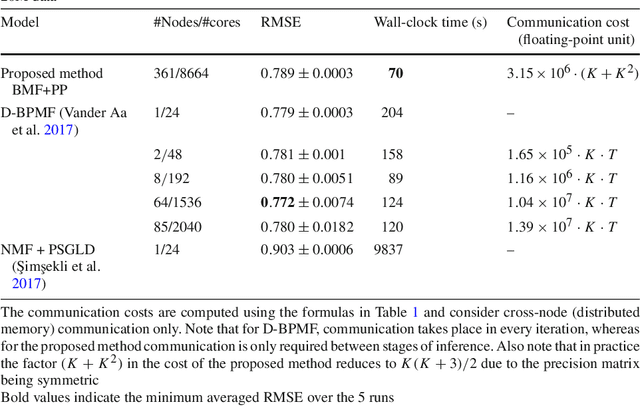
Bayesian matrix factorization (BMF) is a powerful tool for producing low-rank representations of matrices and for predicting missing values and their confidence intervals. Scaling up the posterior inference for massive-scale matrices is challenging and requires distributing both data and computation over many workers, making communication the main computational bottleneck. Embarrassingly parallel inference would remove the communication needed, by using completely independent computations on different data subsets, but suffers from the inherent unidentifiability of BMF solutions. We introduce a hierarchical decomposition of the joint posterior distribution, which couples the subset inferences, allowing for embarrassingly parallel computations in a sequence of at most three stages. Using an efficient approximate implementation, we show empirically on both real and simulated data that our distributed approach is able to achieve a speed-up of almost an order of magnitude, with a negligible effect on predictive accuracy.

Bayesian multi-tensor factorization

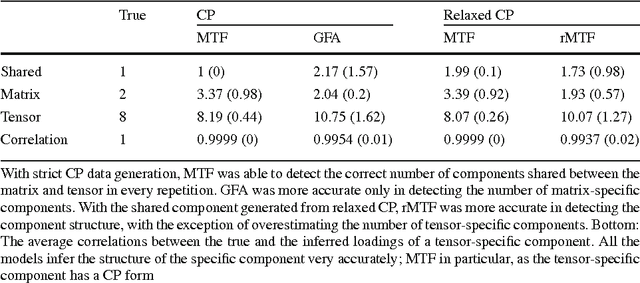
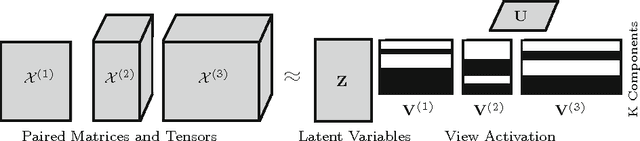
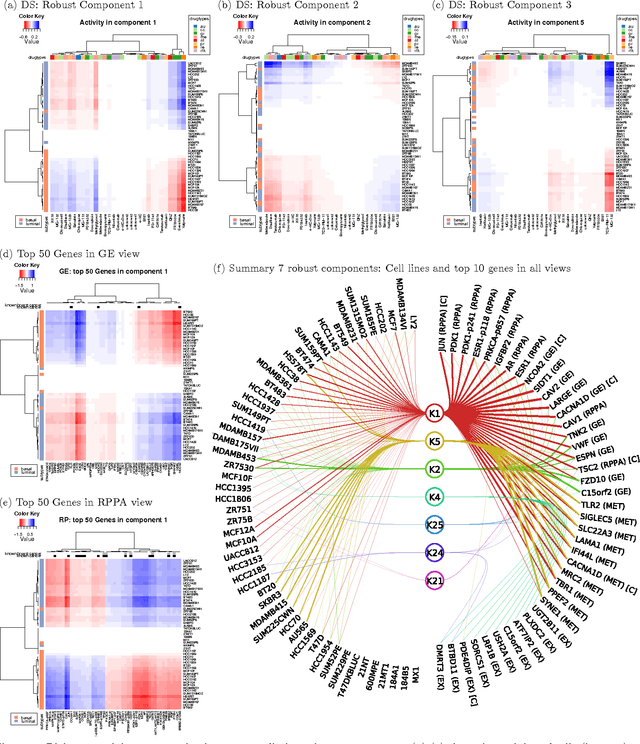
We introduce Bayesian multi-tensor factorization, a model that is the first Bayesian formulation for joint factorization of multiple matrices and tensors. The research problem generalizes the joint matrix-tensor factorization problem to arbitrary sets of tensors of any depth, including matrices, can be interpreted as unsupervised multi-view learning from multiple data tensors, and can be generalized to relax the usual trilinear tensor factorization assumptions. The result is a factorization of the set of tensors into factors shared by any subsets of the tensors, and factors private to individual tensors. We demonstrate the performance against existing baselines in multiple tensor factorization tasks in structural toxicogenomics and functional neuroimaging.

Sparse group factor analysis for biclustering of multiple data sources

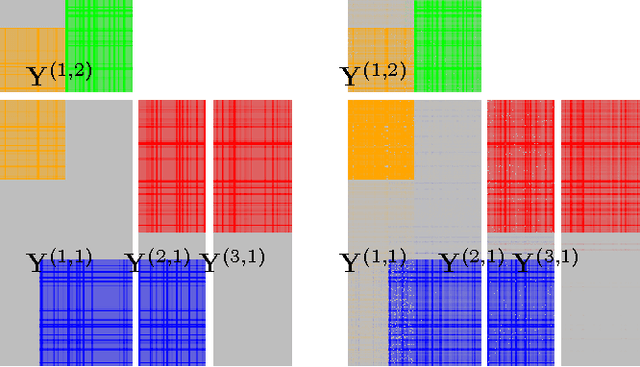
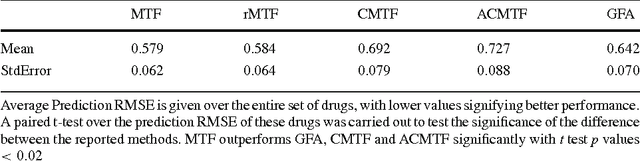
Motivation: Modelling methods that find structure in data are necessary with the current large volumes of genomic data, and there have been various efforts to find subsets of genes exhibiting consistent patterns over subsets of treatments. These biclustering techniques have focused on one data source, often gene expression data. We present a Bayesian approach for joint biclustering of multiple data sources, extending a recent method Group Factor Analysis (GFA) to have a biclustering interpretation with additional sparsity assumptions. The resulting method enables data-driven detection of linear structure present in parts of the data sources. Results: Our simulation studies show that the proposed method reliably infers bi-clusters from heterogeneous data sources. We tested the method on data from the NCI-DREAM drug sensitivity prediction challenge, resulting in an excellent prediction accuracy. Moreover, the predictions are based on several biclusters which provide insight into the data sources, in this case on gene expression, DNA methylation, protein abundance, exome sequence, functional connectivity fingerprints and drug sensitivity.

Group Factor Analysis

Factor analysis provides linear factors that describe relationships between individual variables of a data set. We extend this classical formulation into linear factors that describe relationships between groups of variables, where each group represents either a set of related variables or a data set. The model also naturally extends canonical correlation analysis to more than two sets, in a way that is more flexible than previous extensions. Our solution is formulated as variational inference of a latent variable model with structural sparsity, and it consists of two hierarchical levels: The higher level models the relationships between the groups, whereas the lower models the observed variables given the higher level. We show that the resulting solution solves the group factor analysis problem accurately, outperforming alternative factor analysis based solutions as well as more straightforward implementations of group factor analysis. The method is demonstrated on two life science data sets, one on brain activation and the other on systems biology, illustrating its applicability to the analysis of different types of high-dimensional data sources.