Distributed Bayesian Matrix Factorization with Limited Communication

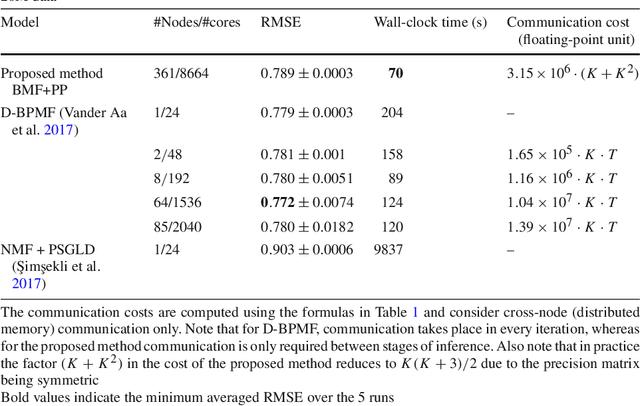
Bayesian matrix factorization (BMF) is a powerful tool for producing low-rank representations of matrices and for predicting missing values and their confidence intervals. Scaling up the posterior inference for massive-scale matrices is challenging and requires distributing both data and computation over many workers, making communication the main computational bottleneck. Embarrassingly parallel inference would remove the communication needed, by using completely independent computations on different data subsets, but suffers from the inherent unidentifiability of BMF solutions. We introduce a hierarchical decomposition of the joint posterior distribution, which couples the subset inferences, allowing for embarrassingly parallel computations in a sequence of at most three stages. Using an efficient approximate implementation, we show empirically on both real and simulated data that our distributed approach is able to achieve a speed-up of almost an order of magnitude, with a negligible effect on predictive accuracy.