Xiangju Qin
A High-Performance Implementation of Bayesian Matrix Factorization with Limited Communication
Apr 14, 2020



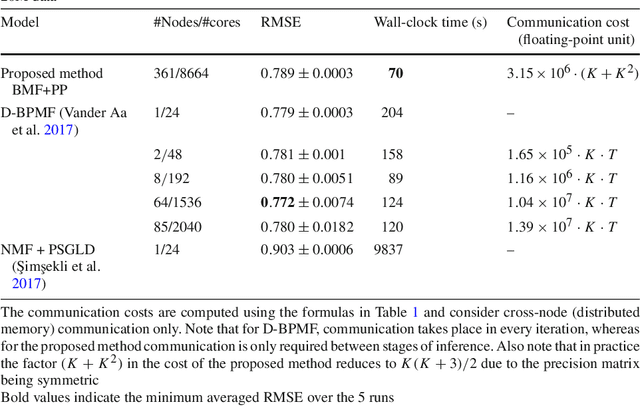
Abstract:Matrix factorization is a very common machine learning technique in recommender systems. Bayesian Matrix Factorization (BMF) algorithms would be attractive because of their ability to quantify uncertainty in their predictions and avoid over-fitting, combined with high prediction accuracy. However, they have not been widely used on large-scale data because of their prohibitive computational cost. In recent work, efforts have been made to reduce the cost, both by improving the scalability of the BMF algorithm as well as its implementation, but so far mainly separately. In this paper we show that the state-of-the-art of both approaches to scalability can be combined. We combine the recent highly-scalable Posterior Propagation algorithm for BMF, which parallelizes computation of blocks of the matrix, with a distributed BMF implementation that users asynchronous communication within each block. We show that the combination of the two methods gives substantial improvements in the scalability of BMF on web-scale datasets, when the goal is to reduce the wall-clock time.
Scalable Bayesian Non-linear Matrix Completion
Jul 31, 2019


Abstract:Matrix completion aims to predict missing elements in a partially observed data matrix which in typical applications, such as collaborative filtering, is large and extremely sparsely observed. A standard solution is matrix factorization, which predicts unobserved entries as linear combinations of latent variables. We generalize to non-linear combinations in massive-scale matrices. Bayesian approaches have been proven beneficial in linear matrix completion, but not applied in the more general non-linear case, due to limited scalability. We introduce a Bayesian non-linear matrix completion algorithm, which is based on a recent Bayesian formulation of Gaussian process latent variable models. To solve the challenges regarding scalability and computation, we propose a data-parallel distributed computational approach with a restricted communication scheme. We evaluate our method on challenging out-of-matrix prediction tasks using both simulated and real-world data.
Distributed Bayesian Matrix Factorization with Limited Communication
Feb 13, 2018


Abstract:Bayesian matrix factorization (BMF) is a powerful tool for producing low-rank representations of matrices and for predicting missing values and their confidence intervals. Scaling up the posterior inference for massive-scale matrices is challenging and requires distributing both data and computation over many workers, making communication the main computational bottleneck. Embarrassingly parallel inference would remove the communication needed, by using completely independent computations on different data subsets, but suffers from the inherent unidentifiability of BMF solutions. We introduce a hierarchical decomposition of the joint posterior distribution, which couples the subset inferences, allowing for embarrassingly parallel computations in a sequence of at most three stages. Using an efficient approximate implementation, we show empirically on both real and simulated data that our distributed approach is able to achieve a speed-up of almost an order of magnitude, with a negligible effect on predictive accuracy.
A Latent Space Analysis of Editor Lifecycles in Wikipedia
Jul 29, 2014



Abstract:Collaborations such as Wikipedia are a key part of the value of the modern Internet. At the same time there is concern that these collaborations are threatened by high levels of member turnover. In this paper we borrow ideas from topic analysis to editor activity on Wikipedia over time into a latent space that offers an insight into the evolving patterns of editor behavior. This latent space representation reveals a number of different categories of editor (e.g. content experts, social networkers) and we show that it does provide a signal that predicts an editor's departure from the community. We also show that long term editors gradually diversify their participation by shifting edit preference from one or two namespaces to multiple namespaces and experience relatively soft evolution in their editor profiles, while short term editors generally distribute their contribution randomly among the namespaces and experience considerably fluctuated evolution in their editor profiles.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge