Simplex-to-Euclidean Bijection for Conjugate and Calibrated Multiclass Gaussian Process

We propose a conjugate and calibrated Gaussian process (GP) model for multi-class classification by exploiting the geometry of the probability simplex. Our approach uses Aitchison geometry to map simplex-valued class probabilities to an unconstrained Euclidean representation, turning classification into a GP regression problem with fewer latent dimensions than standard multi-class GP classifiers. This yields conjugate inference and reliable predictive probabilities without relying on distributional approximations in the model construction. The method is compatible with standard sparse GP regression techniques, enabling scalable inference on larger datasets. Empirical results show well-calibrated and competitive performance across synthetic and real-world datasets.

Point-Identification of a Robust Predictor Under Latent Shift with Imperfect Proxies

Addressing the domain adaptation problem becomes more challenging when distribution shifts across domains stem from latent confounders that affect both covariates and outcomes. Existing proxy-based approaches that address latent shift rely on a strong completeness assumption to uniquely determine (point-identify) a robust predictor. Completeness requires that proxies have sufficient information about variations in latent confounders. For imperfect proxies the mapping from confounders to the space of proxy distributions is non-injective, and multiple latent confounder values can generate the same proxy distribution. This breaks the completeness assumption and observed data are consistent with multiple potential predictors (set-identified). To address this, we introduce latent equivalent classes (LECs). LECs are defined as groups of latent confounders that induce the same conditional proxy distribution. We show that point-identification for the robust predictor remains achievable as long as multiple domains differ sufficiently in how they mix proxy-induced LECs to form the robust predictor. This domain diversity condition is formalized as a cross-domain rank condition on the mixture weights, which is substantially weaker assumption than completeness. We introduce the Proximal Quasi-Bayesian Active learning (PQAL) framework, which actively queries a minimal set of diverse domains that satisfy this rank condition. PQAL can efficiently recover the point-identified predictor, demonstrates robustness to varying degrees of shift and outperforms previous methods on synthetic data and semi-synthetic dSprites dataset.

Consecutive Preferential Bayesian Optimization

Preferential Bayesian optimization allows optimization of objectives that are either expensive or difficult to measure directly, by relying on a minimal number of comparative evaluations done by a human expert. Generating candidate solutions for evaluation is also often expensive, but this cost is ignored by existing methods. We generalize preference-based optimization to explicitly account for production and evaluation costs with Consecutive Preferential Bayesian Optimization, reducing production cost by constraining comparisons to involve previously generated candidates. We also account for the perceptual ambiguity of the oracle providing the feedback by incorporating a Just-Noticeable Difference threshold into a probabilistic preference model to capture indifference to small utility differences. We adapt an information-theoretic acquisition strategy to this setting, selecting new configurations that are most informative about the unknown optimum under a preference model accounting for the perceptual ambiguity. We empirically demonstrate a notable increase in accuracy in setups with high production costs or with indifference feedback.

Simplex-to-Euclidean Bijections for Categorical Flow Matching

We propose a method for learning and sampling from probability distributions supported on the simplex. Our approach maps the open simplex to Euclidean space via smooth bijections, leveraging the Aitchison geometry to define the mappings, and supports modeling categorical data by a Dirichlet interpolation that dequantizes discrete observations into continuous ones. This enables density modeling in Euclidean space through the bijection while still allowing exact recovery of the original discrete distribution. Compared to previous methods that operate on the simplex using Riemannian geometry or custom noise processes, our approach works in Euclidean space while respecting the Aitchison geometry, and achieves competitive performance on both synthetic and real-world data sets.

On the Identifiability of Tensor Ranks via Prior Predictive Matching

Selecting the latent dimensions (ranks) in tensor factorization is a central challenge that often relies on heuristic methods. This paper introduces a rigorous approach to determine rank identifiability in probabilistic tensor models, based on prior predictive moment matching. We transform a set of moment matching conditions into a log-linear system of equations in terms of marginal moments, prior hyperparameters, and ranks; establishing an equivalence between rank identifiability and the solvability of such system. We apply this framework to four foundational tensor-models, demonstrating that the linear structure of the PARAFAC/CP model, the chain structure of the Tensor Train model, and the closed-loop structure of the Tensor Ring model yield solvable systems, making their ranks identifiable. In contrast, we prove that the symmetric topology of the Tucker model leads to an underdetermined system, rendering the ranks unidentifiable by this method. For the identifiable models, we derive explicit closed-form rank estimators based on the moments of observed data only. We empirically validate these estimators and evaluate the robustness of the proposal.

Learning geometry and topology via multi-chart flows

Real world data often lie on low-dimensional Riemannian manifolds embedded in high-dimensional spaces. This motivates learning degenerate normalizing flows that map between the ambient space and a low-dimensional latent space. However, if the manifold has a non-trivial topology, it can never be correctly learned using a single flow. Instead multiple flows must be `glued together'. In this paper, we first propose the general training scheme for learning such a collection of flows, and secondly we develop the first numerical algorithms for computing geodesics on such manifolds. Empirically, we demonstrate that this leads to highly significant improvements in topology estimation.

Geodesic Slice Sampler for Multimodal Distributions with Strong Curvature

Traditional Markov Chain Monte Carlo sampling methods often struggle with sharp curvatures, intricate geometries, and multimodal distributions. Slice sampling can resolve local exploration inefficiency issues and Riemannian geometries help with sharp curvatures. Recent extensions enable slice sampling on Riemannian manifolds, but they are restricted to cases where geodesics are available in closed form. We propose a method that generalizes Hit-and-Run slice sampling to more general geometries tailored to the target distribution, by approximating geodesics as solutions to differential equations. Our approach enables exploration of regions with strong curvature and rapid transitions between modes in multimodal distributions. We demonstrate the advantages of the approach over challenging sampling problems.

Density Ratio Estimation with Conditional Probability Paths

Density ratio estimation in high dimensions can be reframed as integrating a certain quantity, the time score, over probability paths which interpolate between the two densities. In practice, the time score has to be estimated based on samples from the two densities. However, existing methods for this problem remain computationally expensive and can yield inaccurate estimates. Inspired by recent advances in generative modeling, we introduce a novel framework for time score estimation, based on a conditioning variable. Choosing the conditioning variable judiciously enables a closed-form objective function. We demonstrate that, compared to previous approaches, our approach results in faster learning of the time score and competitive or better estimation accuracies of the density ratio on challenging tasks. Furthermore, we establish theoretical guarantees on the error of the estimated density ratio.

Preferential Normalizing Flows

Eliciting a high-dimensional probability distribution from an expert via noisy judgments is notoriously challenging, yet useful for many applications, such as prior elicitation and reward modeling. We introduce a method for eliciting the expert's belief density as a normalizing flow based solely on preferential questions such as comparing or ranking alternatives. This allows eliciting in principle arbitrarily flexible densities, but flow estimation is susceptible to the challenge of collapsing or diverging probability mass that makes it difficult in practice. We tackle this problem by introducing a novel functional prior for the flow, motivated by a decision-theoretic argument, and show empirically that the belief density can be inferred as the function-space maximum a posteriori estimate. We demonstrate our method by eliciting multivariate belief densities of simulated experts, including the prior belief of a general-purpose large language model over a real-world dataset.

Stochastic variance-reduced Gaussian variational inference on the Bures-Wasserstein manifold

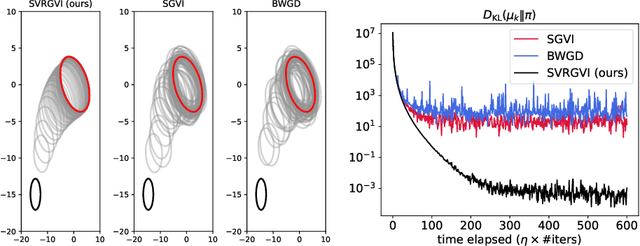
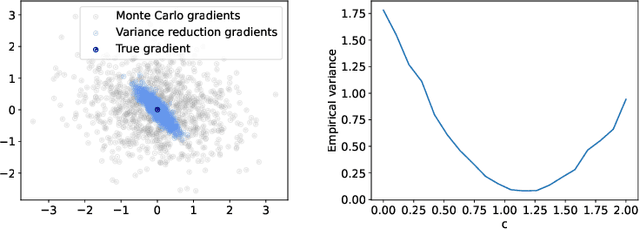
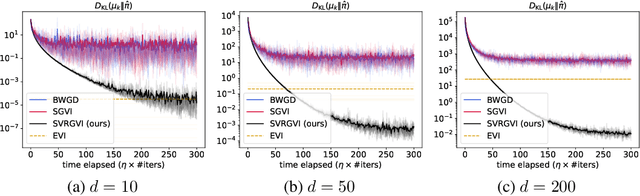
Optimization in the Bures-Wasserstein space has been gaining popularity in the machine learning community since it draws connections between variational inference and Wasserstein gradient flows. The variational inference objective function of Kullback-Leibler divergence can be written as the sum of the negative entropy and the potential energy, making forward-backward Euler the method of choice. Notably, the backward step admits a closed-form solution in this case, facilitating the practicality of the scheme. However, the forward step is no longer exact since the Bures-Wasserstein gradient of the potential energy involves "intractable" expectations. Recent approaches propose using the Monte Carlo method -- in practice a single-sample estimator -- to approximate these terms, resulting in high variance and poor performance. We propose a novel variance-reduced estimator based on the principle of control variates. We theoretically show that this estimator has a smaller variance than the Monte-Carlo estimator in scenarios of interest. We also prove that variance reduction helps improve the optimization bounds of the current analysis. We demonstrate that the proposed estimator gains order-of-magnitude improvements over the previous Bures-Wasserstein methods.