Normalizing Flow Regression for Bayesian Inference with Offline Likelihood Evaluations

Bayesian inference with computationally expensive likelihood evaluations remains a significant challenge in many scientific domains. We propose normalizing flow regression (NFR), a novel offline inference method for approximating posterior distributions. Unlike traditional surrogate approaches that require additional sampling or inference steps, NFR directly yields a tractable posterior approximation through regression on existing log-density evaluations. We introduce training techniques specifically for flow regression, such as tailored priors and likelihood functions, to achieve robust posterior and model evidence estimation. We demonstrate NFR's effectiveness on synthetic benchmarks and real-world applications from neuroscience and biology, showing superior or comparable performance to existing methods. NFR represents a promising approach for Bayesian inference when standard methods are computationally prohibitive or existing model evaluations can be recycled.

Preferential Normalizing Flows

Eliciting a high-dimensional probability distribution from an expert via noisy judgments is notoriously challenging, yet useful for many applications, such as prior elicitation and reward modeling. We introduce a method for eliciting the expert's belief density as a normalizing flow based solely on preferential questions such as comparing or ranking alternatives. This allows eliciting in principle arbitrarily flexible densities, but flow estimation is susceptible to the challenge of collapsing or diverging probability mass that makes it difficult in practice. We tackle this problem by introducing a novel functional prior for the flow, motivated by a decision-theoretic argument, and show empirically that the belief density can be inferred as the function-space maximum a posteriori estimate. We demonstrate our method by eliciting multivariate belief densities of simulated experts, including the prior belief of a general-purpose large language model over a real-world dataset.

Non-geodesically-convex optimization in the Wasserstein space

We study a class of optimization problems in the Wasserstein space (the space of probability measures) where the objective function is \emph{nonconvex} along generalized geodesics. When the regularization term is the negative entropy, the optimization problem becomes a sampling problem where it minimizes the Kullback-Leibler divergence between a probability measure (optimization variable) and a target probability measure whose logarithmic probability density is a nonconvex function. We derive multiple convergence insights for a novel {\em semi Forward-Backward Euler scheme} under several nonconvex (and possibly nonsmooth) regimes. Notably, the semi Forward-Backward Euler is just a slight modification of the Forward-Backward Euler whose convergence is -- to our knowledge -- still unknown in our very general non-geodesically-convex setting.

Cooperative Bayesian Optimization for Imperfect Agents

We introduce a cooperative Bayesian optimization problem for optimizing black-box functions of two variables where two agents choose together at which points to query the function but have only control over one variable each. This setting is inspired by human-AI teamwork, where an AI-assistant helps its human user solve a problem, in this simplest case, collaborative optimization. We formulate the solution as sequential decision-making, where the agent we control models the user as a computationally rational agent with prior knowledge about the function. We show that strategic planning of the queries enables better identification of the global maximum of the function as long as the user avoids excessive exploration. This planning is made possible by using Bayes Adaptive Monte Carlo planning and by endowing the agent with a user model that accounts for conservative belief updates and exploratory sampling of the points to query.

Multi-Fidelity Bayesian Optimization with Unreliable Information Sources

Bayesian optimization (BO) is a powerful framework for optimizing black-box, expensive-to-evaluate functions. Over the past decade, many algorithms have been proposed to integrate cheaper, lower-fidelity approximations of the objective function into the optimization process, with the goal of converging towards the global optimum at a reduced cost. This task is generally referred to as multi-fidelity Bayesian optimization (MFBO). However, MFBO algorithms can lead to higher optimization costs than their vanilla BO counterparts, especially when the low-fidelity sources are poor approximations of the objective function, therefore defeating their purpose. To address this issue, we propose rMFBO (robust MFBO), a methodology to make any GP-based MFBO scheme robust to the addition of unreliable information sources. rMFBO comes with a theoretical guarantee that its performance can be bound to its vanilla BO analog, with high controllable probability. We demonstrate the effectiveness of the proposed methodology on a number of numerical benchmarks, outperforming earlier MFBO methods on unreliable sources. We expect rMFBO to be particularly useful to reliably include human experts with varying knowledge within BO processes.

Bayesian Optimization Augmented with Actively Elicited Expert Knowledge

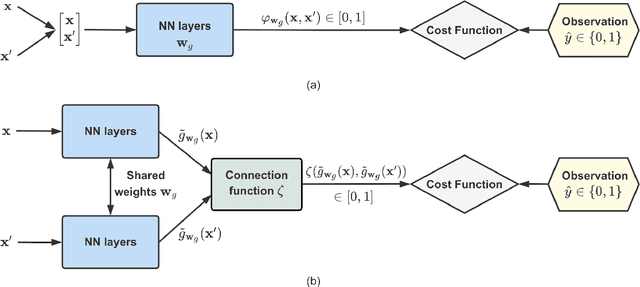
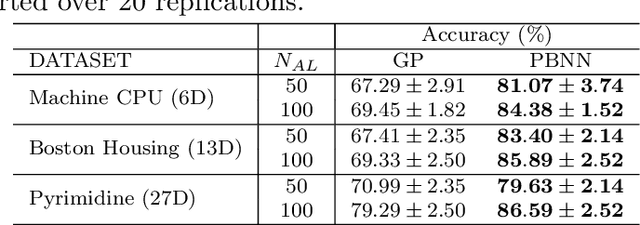
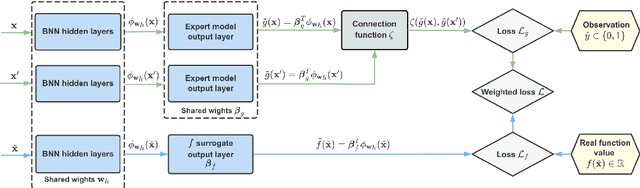
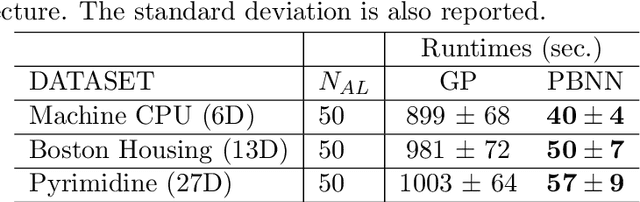
Bayesian optimization (BO) is a well-established method to optimize black-box functions whose direct evaluations are costly. In this paper, we tackle the problem of incorporating expert knowledge into BO, with the goal of further accelerating the optimization, which has received very little attention so far. We design a multi-task learning architecture for this task, with the goal of jointly eliciting the expert knowledge and minimizing the objective function. In particular, this allows for the expert knowledge to be transferred into the BO task. We introduce a specific architecture based on Siamese neural networks to handle the knowledge elicitation from pairwise queries. Experiments on various benchmark functions with both simulated and actual human experts show that the proposed method significantly speeds up BO even when the expert knowledge is biased compared to the objective function.

Targeted Active Learning for Bayesian Decision-Making

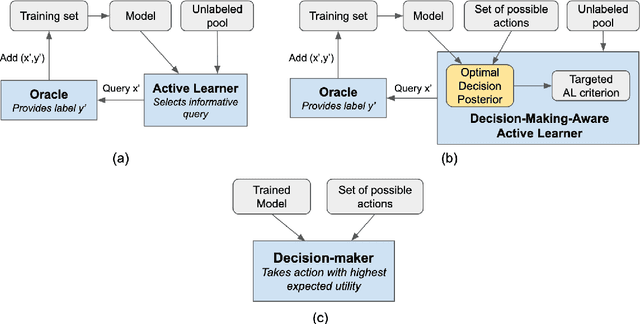
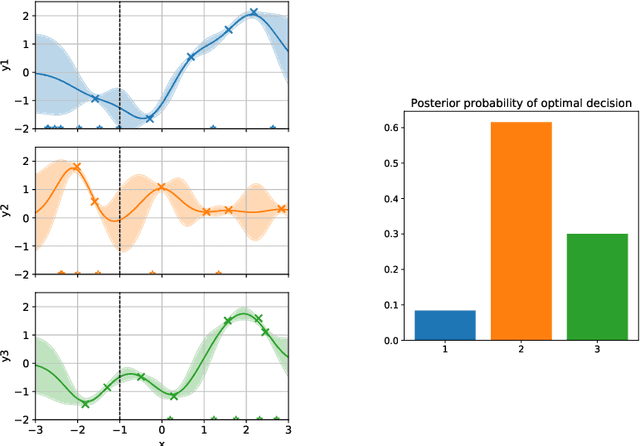
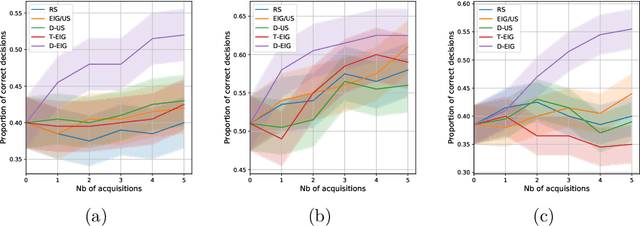
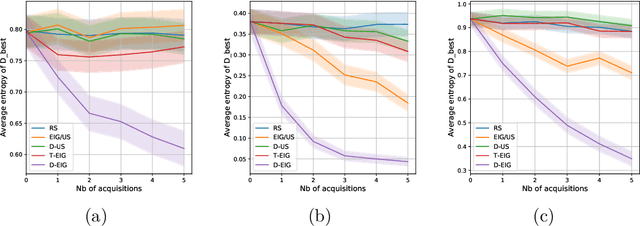
Active learning is usually applied to acquire labels of informative data points in supervised learning, to maximize accuracy in a sample-efficient way. However, maximizing the accuracy is not the end goal when the results are used for decision-making, for example in personalized medicine or economics. We argue that when acquiring samples sequentially, separating learning and decision-making is sub-optimal, and we introduce a novel active learning strategy which takes the down-the-line decision problem into account. Specifically, we introduce a novel active learning criterion which maximizes the expected information gain on the posterior distribution of the optimal decision. We compare our decision-making-aware active learning strategy to existing alternatives on both simulated and real data, and show improved performance in decision-making accuracy.

Projective Preferential Bayesian Optimization

Bayesian optimization is an effective method for finding extrema of a black-box function. We propose a new type of Bayesian optimization for learning user preferences in high-dimensional spaces. The central assumption is that the underlying objective function cannot be evaluated directly, but instead a minimizer along a projection can be queried, which we call a projective preferential query. The form of the query allows for feedback that is natural for a human to give, and which enables interaction. This is demonstrated in a user experiment in which the user feedback comes in the form of optimal position and orientation of a molecule adsorbing to a surface. We demonstrate that our framework is able to find a global minimum of a high-dimensional black-box function, which is an infeasible task for existing preferential Bayesian optimization frameworks that are based on pairwise comparisons.