Louis Filstroff
Cost-aware learning of relevant contextual variables within Bayesian optimization
May 24, 2023

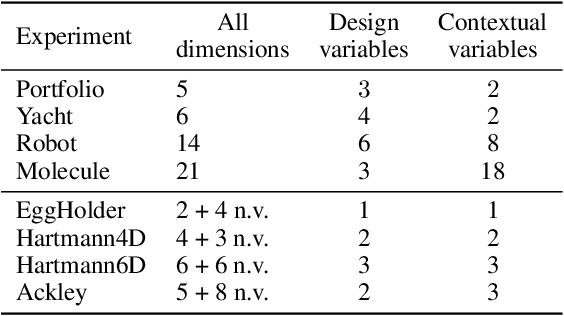

Abstract:Contextual Bayesian Optimization (CBO) is a powerful framework for optimizing black-box, expensive-to-evaluate functions with respect to design variables, while simultaneously efficiently integrating relevant contextual information regarding the environment, such as experimental conditions. However, in many practical scenarios, the relevance of contextual variables is not necessarily known beforehand. Moreover, the contextual variables can sometimes be optimized themselves, a setting that current CBO algorithms do not take into account. Optimizing contextual variables may be costly, which raises the question of determining a minimal relevant subset. In this paper, we frame this problem as a cost-aware model selection BO task and address it using a novel method, Sensitivity-Analysis-Driven Contextual BO (SADCBO). We learn the relevance of context variables by sensitivity analysis of the posterior surrogate model at specific input points, whilst minimizing the cost of optimization by leveraging recent developments on early stopping for BO. We empirically evaluate our proposed SADCBO against alternatives on synthetic experiments together with extensive ablation studies, and demonstrate a consistent improvement across examples.
Multi-Fidelity Bayesian Optimization with Unreliable Information Sources
Oct 25, 2022Abstract:Bayesian optimization (BO) is a powerful framework for optimizing black-box, expensive-to-evaluate functions. Over the past decade, many algorithms have been proposed to integrate cheaper, lower-fidelity approximations of the objective function into the optimization process, with the goal of converging towards the global optimum at a reduced cost. This task is generally referred to as multi-fidelity Bayesian optimization (MFBO). However, MFBO algorithms can lead to higher optimization costs than their vanilla BO counterparts, especially when the low-fidelity sources are poor approximations of the objective function, therefore defeating their purpose. To address this issue, we propose rMFBO (robust MFBO), a methodology to make any GP-based MFBO scheme robust to the addition of unreliable information sources. rMFBO comes with a theoretical guarantee that its performance can be bound to its vanilla BO analog, with high controllable probability. We demonstrate the effectiveness of the proposed methodology on a number of numerical benchmarks, outperforming earlier MFBO methods on unreliable sources. We expect rMFBO to be particularly useful to reliably include human experts with varying knowledge within BO processes.
Bayesian Optimization Augmented with Actively Elicited Expert Knowledge
Aug 18, 2022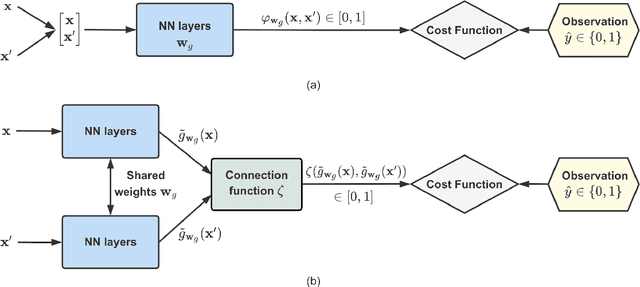
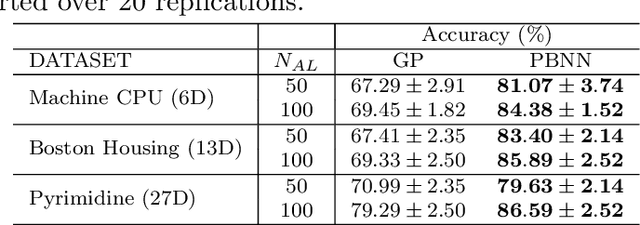
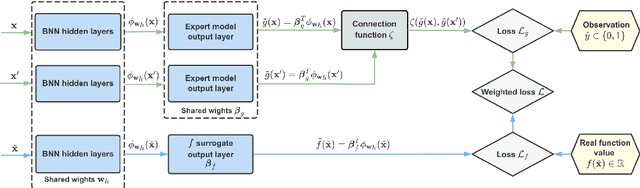
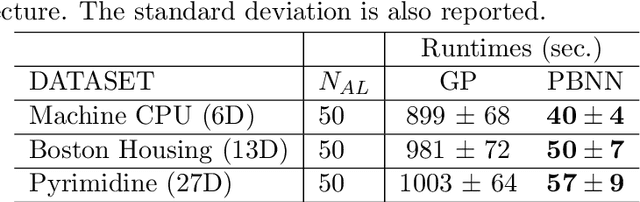
Abstract:Bayesian optimization (BO) is a well-established method to optimize black-box functions whose direct evaluations are costly. In this paper, we tackle the problem of incorporating expert knowledge into BO, with the goal of further accelerating the optimization, which has received very little attention so far. We design a multi-task learning architecture for this task, with the goal of jointly eliciting the expert knowledge and minimizing the objective function. In particular, this allows for the expert knowledge to be transferred into the BO task. We introduce a specific architecture based on Siamese neural networks to handle the knowledge elicitation from pairwise queries. Experiments on various benchmark functions with both simulated and actual human experts show that the proposed method significantly speeds up BO even when the expert knowledge is biased compared to the objective function.
Approximate Bayesian Computation with Domain Expert in the Loop
Jan 28, 2022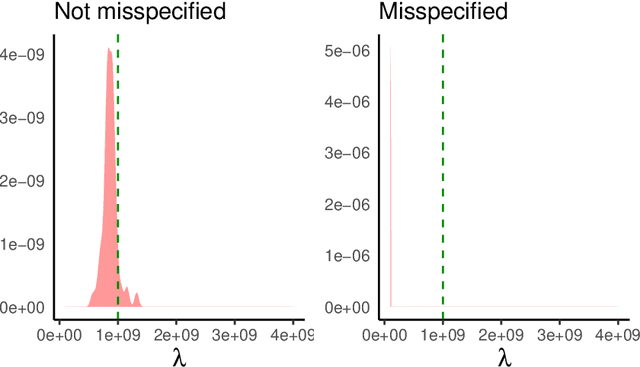

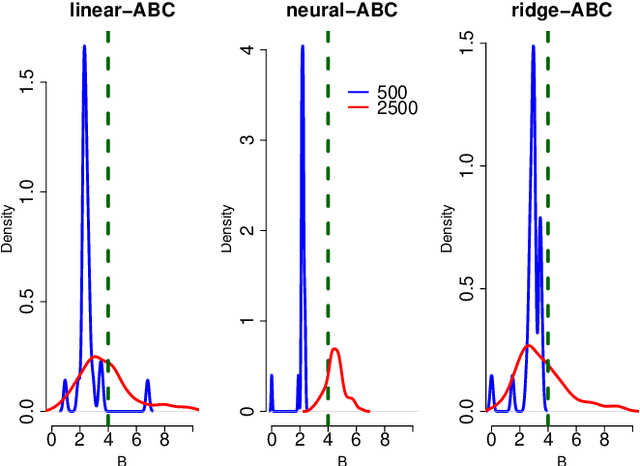

Abstract:Approximate Bayesian computation (ABC) is a popular likelihood-free inference method for models with intractable likelihood functions. As ABC methods usually rely on comparing summary statistics of observed and simulated data, the choice of the statistics is crucial. This choice involves a trade-off between loss of information and dimensionality reduction, and is often determined based on domain knowledge. However, handcrafting and selecting suitable statistics is a laborious task involving multiple trial-and-error steps. In this work, we introduce an active learning method for ABC statistics selection which reduces the domain expert's work considerably. By involving the experts, we are able to handle misspecified models, unlike the existing dimension reduction methods. Moreover, empirical results show better posterior estimates than with existing methods, when the simulation budget is limited.
Targeted Active Learning for Bayesian Decision-Making
Jun 08, 2021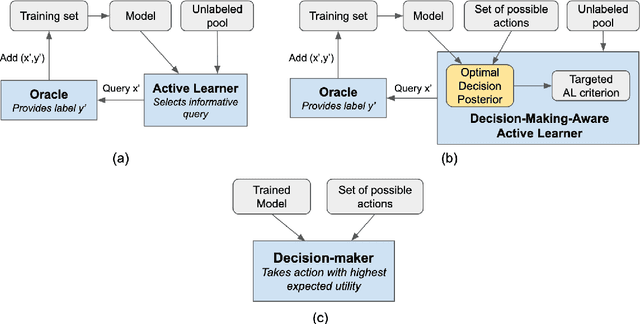
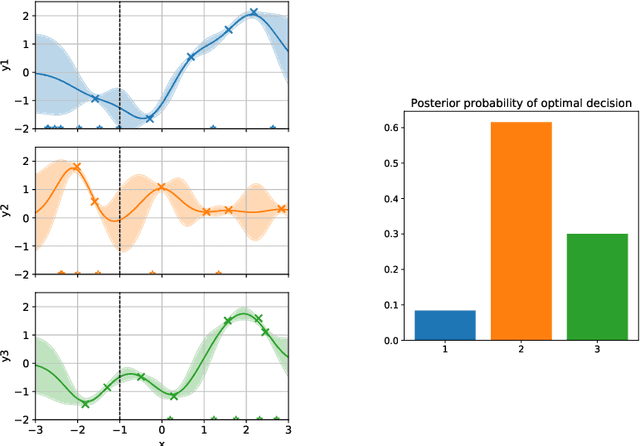
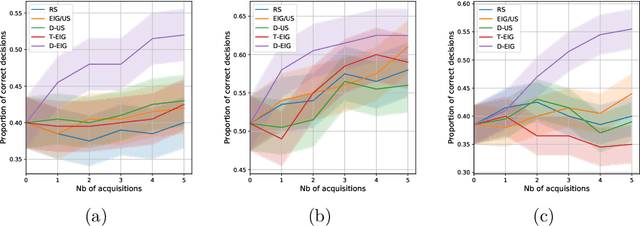
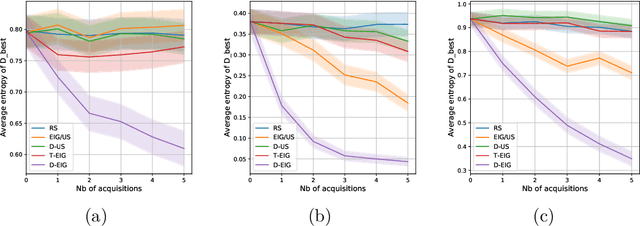
Abstract:Active learning is usually applied to acquire labels of informative data points in supervised learning, to maximize accuracy in a sample-efficient way. However, maximizing the accuracy is not the end goal when the results are used for decision-making, for example in personalized medicine or economics. We argue that when acquiring samples sequentially, separating learning and decision-making is sub-optimal, and we introduce a novel active learning strategy which takes the down-the-line decision problem into account. Specifically, we introduce a novel active learning criterion which maximizes the expected information gain on the posterior distribution of the optimal decision. We compare our decision-making-aware active learning strategy to existing alternatives on both simulated and real data, and show improved performance in decision-making accuracy.
A Comparative Study of Temporal Non-Negative Matrix Factorization with Gamma Markov Chains
Jun 23, 2020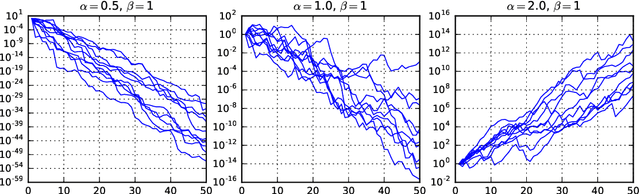

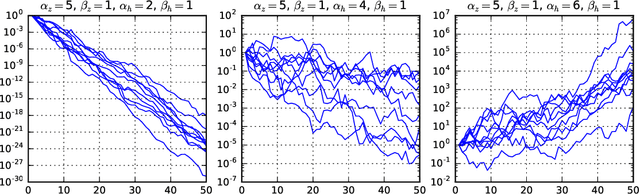

Abstract:Non-negative matrix factorization (NMF) has become a well-established class of methods for the analysis of non-negative data. In particular, a lot of effort has been devoted to probabilistic NMF, namely estimation or inference tasks in probabilistic models describing the data, based for example on Poisson or exponential likelihoods. When dealing with time series data, several works have proposed to model the evolution of the activation coefficients as a non-negative Markov chain, most of the time in relation with the Gamma distribution, giving rise to so-called temporal NMF models. In this paper, we review three Gamma Markov chains of the NMF literature, and show that they all share the same drawback: the absence of a well-defined stationary distribution. We then introduce a fourth process, an overlooked model of the time series literature named BGAR(1), which overcomes this limitation. These four temporal NMF models are then compared in a MAP framework on a prediction task, in the context of the Poisson likelihood.
A Ranking Model Motivated by Nonnegative Matrix Factorization with Applications to Tennis Tournaments
Mar 15, 2019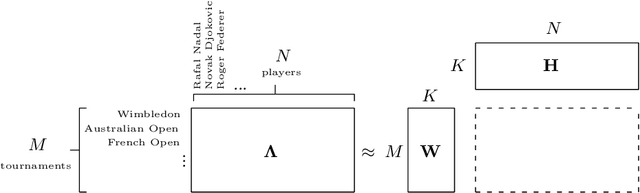
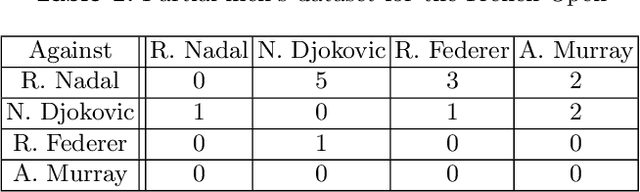
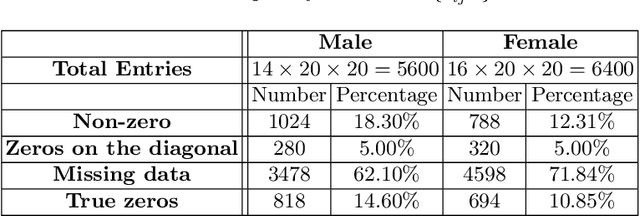
Abstract:We propose a novel ranking model that combines the Bradley-Terry-Luce probability model with a nonnegative matrix factorization framework to model and uncover the presence of latent variables that influence the performance of top tennis players. We derive an efficient, provably convergent, and numerically stable majorization-minimization-based algorithm to maximize the likelihood of datasets under the proposed statistical model. The model is tested on datasets involving the outcomes of matches between 20 top male and female tennis players over 14 major tournaments for men (including the Grand Slams and the ATP Masters 1000) and 16 major tournaments for women over the past 10 years. Our model automatically infers that the surface of the court (e.g., clay or hard court) is a key determinant of the performances of male players, but less so for females. Top players on various surfaces over this longitudinal period are also identified in an objective manner.
Bayesian Mean-parameterized Nonnegative Binary Matrix Factorization
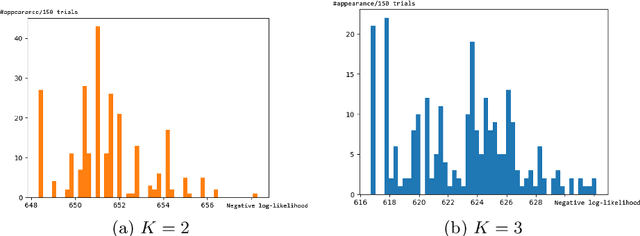
Dec 17, 2018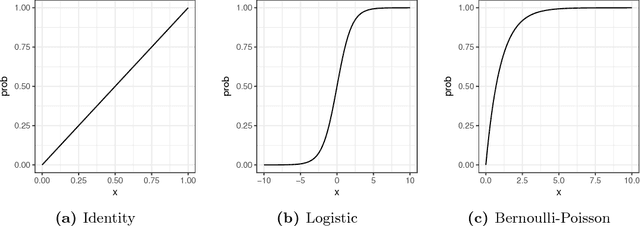
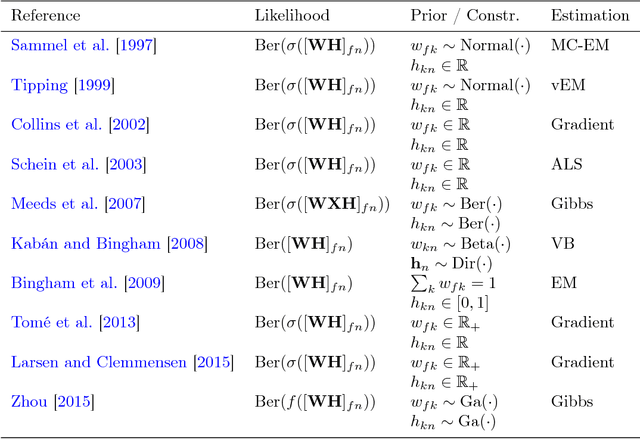

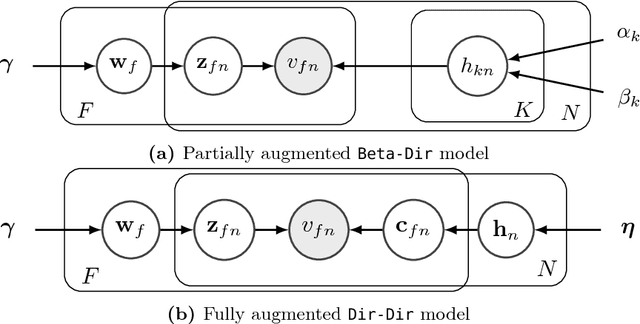
Abstract:Binary data matrices can represent many types of data such as social networks, votes or gene expression. In some cases, the analysis of binary matrices can be tackled with nonnegative matrix factorization (NMF), where the observed data matrix is approximated by the product of two smaller nonnegative matrices. In this context, probabilistic NMF assumes a generative model where the data is usually Bernoulli-distributed. Often, a link function is used to map the factorization to the $[0,1]$ range, ensuring a valid Bernoulli mean parameter. However, link functions have the potential disadvantage to lead to uninterpretable models. Mean-parameterized NMF, on the contrary, overcomes this problem. We propose a unified framework for Bayesian mean-parameterized nonnegative binary matrix factorization models (NBMF). We analyze three models which correspond to three possible constraints that respect the mean-parametrization without the need for link functions. Furthermore, we derive a novel collapsed Gibbs sampler and a collapsed variational algorithm to infer the posterior distribution of the factors. Next, we extend the proposed models to a nonparametric setting where the number of used latent dimensions is automatically driven by the observed data. We analyze the performance of our NBMF methods in multiple datasets for different tasks such as dictionary learning and prediction of missing data. Experiments show that our methods provide similar or superior results than the state of the art, while automatically detecting the number of relevant components.
Closed-form Marginal Likelihood in Gamma-Poisson Matrix Factorization
May 31, 2018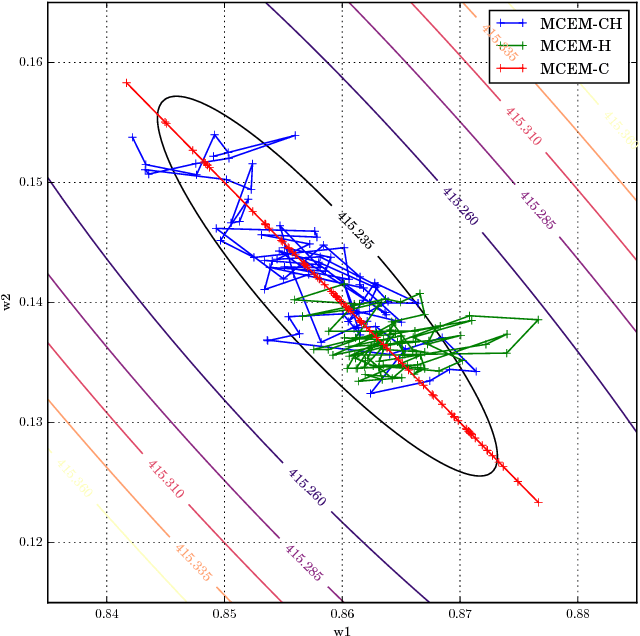
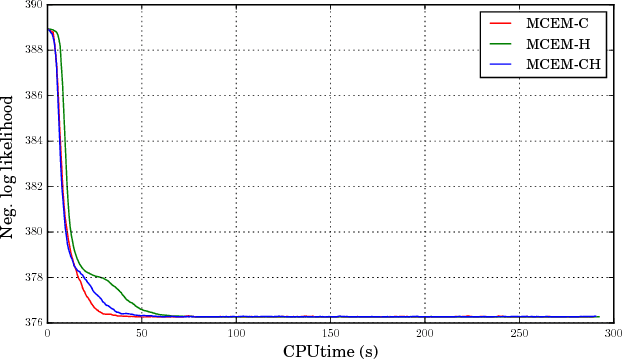
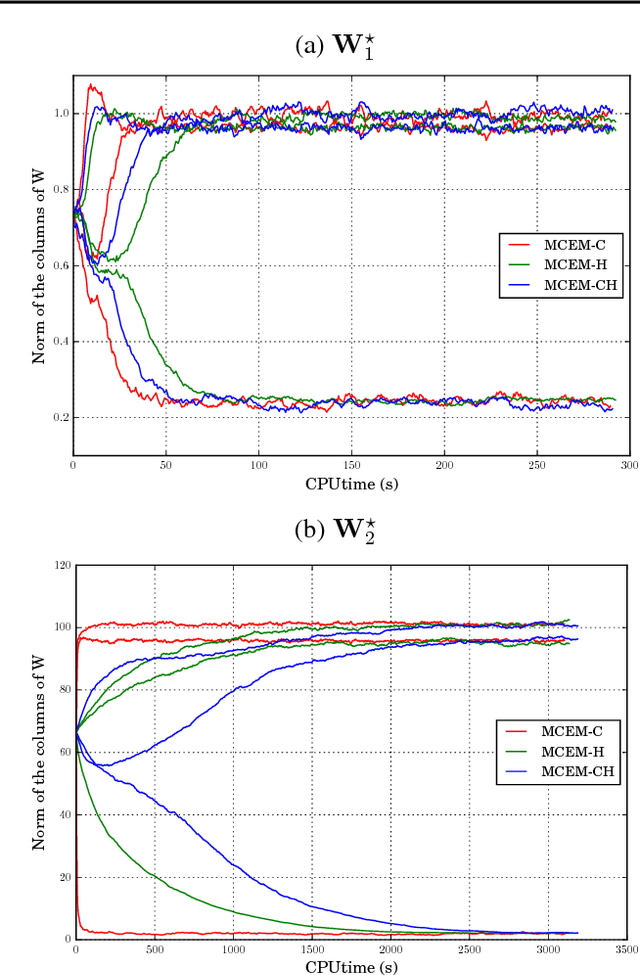
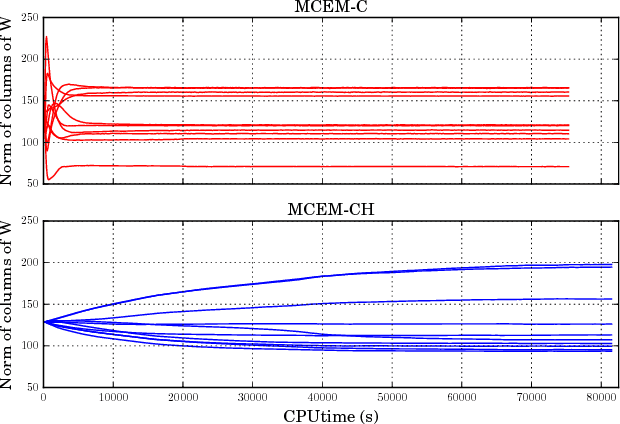
Abstract:We present novel understandings of the Gamma-Poisson (GaP) model, a probabilistic matrix factorization model for count data. We show that GaP can be rewritten free of the score/activation matrix. This gives us new insights about the estimation of the topic/dictionary matrix by maximum marginal likelihood estimation. In particular, this explains the robustness of this estimator to over-specified values of the factorization rank, especially its ability to automatically prune irrelevant dictionary columns, as empirically observed in previous work. The marginalization of the activation matrix leads in turn to a new Monte Carlo Expectation-Maximization algorithm with favorable properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge