The Lucie-7B LLM and the Lucie Training Dataset: Open resources for multilingual language generation

We present both the Lucie Training Dataset and the Lucie-7B foundation model. The Lucie Training Dataset is a multilingual collection of textual corpora centered around French and designed to offset anglo-centric biases found in many datasets for large language model pretraining. Its French data is pulled not only from traditional web sources, but also from French cultural heritage documents, filling an important gap in modern datasets. Beyond French, which makes up the largest share of the data, we added documents to support several other European languages, including English, Spanish, German, and Italian. Apart from its value as a resource for French language and culture, an important feature of this dataset is that it prioritizes data rights by minimizing copyrighted material. In addition, building on the philosophy of past open projects, it is redistributed in the form used for training and its processing is described on Hugging Face and GitHub. The Lucie-7B foundation model is trained on equal amounts of data in French and English -- roughly 33% each -- in an effort to better represent cultural aspects of French-speaking communities. We also describe two instruction fine-tuned models, Lucie-7B-Instruct-v1.1 and Lucie-7B-Instruct-human-data, which we release as demonstrations of Lucie-7B in use. These models achieve promising results compared to state-of-the-art models, demonstrating that an open approach prioritizing data rights can still deliver strong performance. We see these models as an initial step toward developing more performant, aligned models in the near future. Model weights for Lucie-7B and the Lucie instruct models, along with intermediate checkpoints for the former, are published on Hugging Face, while model training and data preparation code is available on GitHub. This makes Lucie-7B one of the first OSI compliant language models according to the new OSI definition.

TEARS: Textual Representations for Scrutable Recommendations

Traditional recommender systems rely on high-dimensional (latent) embeddings for modeling user-item interactions, often resulting in opaque representations that lack interpretability. Moreover, these systems offer limited control to users over their recommendations. Inspired by recent work, we introduce TExtuAl Representations for Scrutable recommendations (TEARS) to address these challenges. Instead of representing a user's interests through a latent embedding, TEARS encodes them in natural text, providing transparency and allowing users to edit them. To do so, TEARS uses a modern LLM to generate user summaries based on user preferences. We find the summaries capture user preferences uniquely. Using these summaries, we take a hybrid approach where we use an optimal transport procedure to align the summaries' representation with the learned representation of a standard VAE for collaborative filtering. We find this approach can surpass the performance of three popular VAE models while providing user-controllable recommendations. We also analyze the controllability of TEARS through three simulated user tasks to evaluate the effectiveness of a user editing its summary.

A Comparative Study of Temporal Non-Negative Matrix Factorization with Gamma Markov Chains

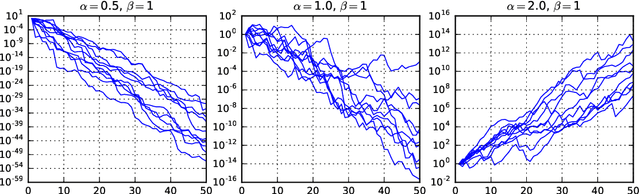
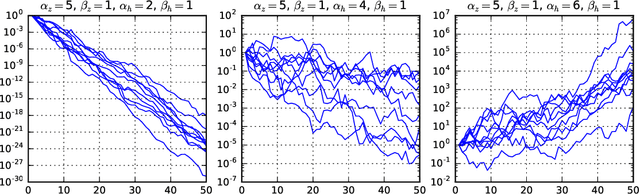
Non-negative matrix factorization (NMF) has become a well-established class of methods for the analysis of non-negative data. In particular, a lot of effort has been devoted to probabilistic NMF, namely estimation or inference tasks in probabilistic models describing the data, based for example on Poisson or exponential likelihoods. When dealing with time series data, several works have proposed to model the evolution of the activation coefficients as a non-negative Markov chain, most of the time in relation with the Gamma distribution, giving rise to so-called temporal NMF models. In this paper, we review three Gamma Markov chains of the NMF literature, and show that they all share the same drawback: the absence of a well-defined stationary distribution. We then introduce a fourth process, an overlooked model of the time series literature named BGAR(1), which overcomes this limitation. These four temporal NMF models are then compared in a MAP framework on a prediction task, in the context of the Poisson likelihood.

Ordinal Non-negative Matrix Factorization for Recommendation

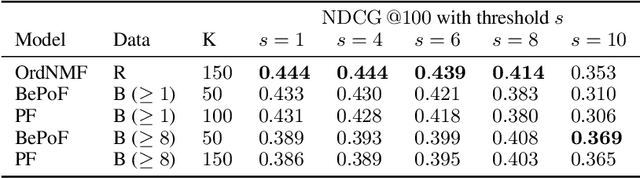
We introduce a new non-negative matrix factorization (NMF) method for ordinal data, called OrdNMF. Ordinal data are categorical data which exhibit a natural ordering between the categories. In particular, they can be found in recommender systems, either with explicit data (such as ratings) or implicit data (such as quantized play counts). OrdNMF is a probabilistic latent factor model that generalizes Bernoulli-Poisson factorization (BePoF) and Poisson factorization (PF) applied to binarized data. Contrary to these methods, OrdNMF circumvents binarization and can exploit a more informative representation of the data. We design an efficient variational algorithm based on a suitable model augmentation and related to variational PF. In particular, our algorithm preserves the scalability of PF and can be applied to huge sparse datasets. We report recommendation experiments on explicit and implicit datasets, and show that OrdNMF outperforms BePoF and PF applied to binarized data.

Recommendation from Raw Data with Adaptive Compound Poisson Factorization

Count data are often used in recommender systems: they are widespread (song play counts, product purchases, clicks on web pages) and can reveal user preference without any explicit rating from the user. Such data are known to be sparse, over-dispersed and bursty, which makes their direct use in recommender systems challenging, often leading to pre-processing steps such as binarization. The aim of this paper is to build recommender systems from these raw data, by means of the recently proposed compound Poisson Factorization (cPF). The paper contributions are three-fold: we present a unified framework for discrete data (dcPF), leading to an adaptive and scalable algorithm; we show that our framework achieves a trade-off between Poisson Factorization (PF) applied to raw and binarized data; we study four specific instances that are relevant to recommendation and exhibit new links with combinatorics. Experiments with three different datasets show that dcPF is able to effectively adjust to over-dispersion, leading to better recommendation scores when compared with PF on either raw or binarized data.

Negative Binomial Matrix Factorization for Recommender Systems

We introduce negative binomial matrix factorization (NBMF), a matrix factorization technique specially designed for analyzing over-dispersed count data. It can be viewed as an extension of Poisson matrix factorization (PF) perturbed by a multiplicative term which models exposure. This term brings a degree of freedom for controlling the dispersion, making NBMF more robust to outliers. We show that NBMF allows to skip traditional pre-processing stages, such as binarization, which lead to loss of information. Two estimation approaches are presented: maximum likelihood and variational Bayes inference. We test our model with a recommendation task and show its ability to predict user tastes with better precision than PF.