Ayush Bharti
ALINE: Joint Amortization for Bayesian Inference and Active Data Acquisition
Jun 08, 2025Abstract:Many critical applications, from autonomous scientific discovery to personalized medicine, demand systems that can both strategically acquire the most informative data and instantaneously perform inference based upon it. While amortized methods for Bayesian inference and experimental design offer part of the solution, neither approach is optimal in the most general and challenging task, where new data needs to be collected for instant inference. To tackle this issue, we introduce the Amortized Active Learning and Inference Engine (ALINE), a unified framework for amortized Bayesian inference and active data acquisition. ALINE leverages a transformer architecture trained via reinforcement learning with a reward based on self-estimated information gain provided by its own integrated inference component. This allows it to strategically query informative data points while simultaneously refining its predictions. Moreover, ALINE can selectively direct its querying strategy towards specific subsets of model parameters or designated predictive tasks, optimizing for posterior estimation, data prediction, or a mixture thereof. Empirical results on regression-based active learning, classical Bayesian experimental design benchmarks, and a psychometric model with selectively targeted parameters demonstrate that ALINE delivers both instant and accurate inference along with efficient selection of informative points.
Multilevel neural simulation-based inference
Jun 06, 2025Abstract:Neural simulation-based inference (SBI) is a popular set of methods for Bayesian inference when models are only available in the form of a simulator. These methods are widely used in the sciences and engineering, where writing down a likelihood can be significantly more challenging than constructing a simulator. However, the performance of neural SBI can suffer when simulators are computationally expensive, thereby limiting the number of simulations that can be performed. In this paper, we propose a novel approach to neural SBI which leverages multilevel Monte Carlo techniques for settings where several simulators of varying cost and fidelity are available. We demonstrate through both theoretical analysis and extensive experiments that our method can significantly enhance the accuracy of SBI methods given a fixed computational budget.
Robust Simulation-Based Inference under Missing Data via Neural Processes
Mar 03, 2025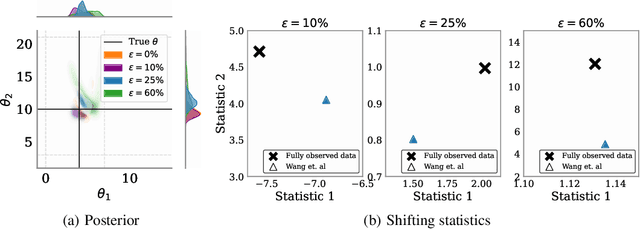

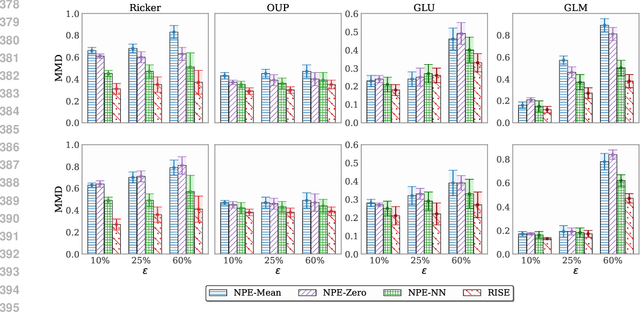
Abstract:Simulation-based inference (SBI) methods typically require fully observed data to infer parameters of models with intractable likelihood functions. However, datasets often contain missing values due to incomplete observations, data corruptions (common in astrophysics), or instrument limitations (e.g., in high-energy physics applications). In such scenarios, missing data must be imputed before applying any SBI method. We formalize the problem of missing data in SBI and demonstrate that naive imputation methods can introduce bias in the estimation of SBI posterior. We also introduce a novel amortized method that addresses this issue by jointly learning the imputation model and the inference network within a neural posterior estimation (NPE) framework. Extensive empirical results on SBI benchmarks show that our approach provides robust inference outcomes compared to standard baselines for varying levels of missing data. Moreover, we demonstrate the merits of our imputation model on two real-world bioactivity datasets (Adrenergic and Kinase assays). Code is available at https://github.com/Aalto-QuML/RISE.
Cost-aware Simulation-based Inference
Oct 10, 2024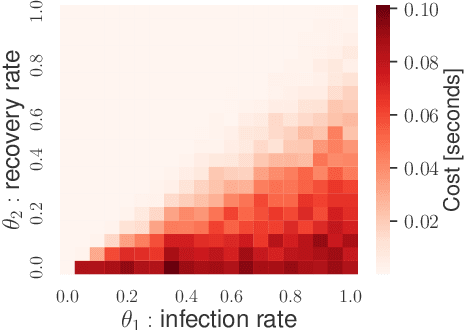
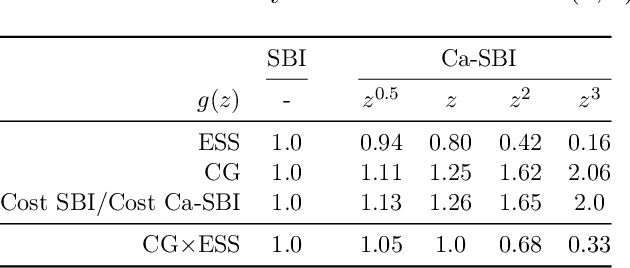
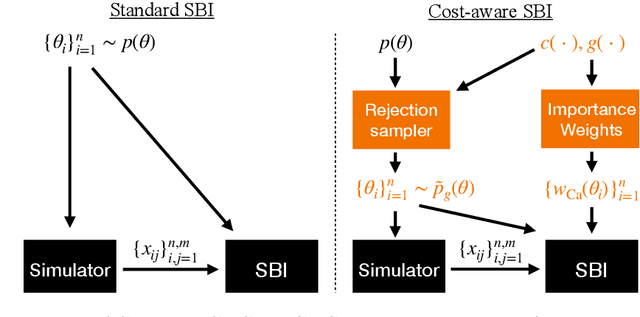

Abstract:Simulation-based inference (SBI) is the preferred framework for estimating parameters of intractable models in science and engineering. A significant challenge in this context is the large computational cost of simulating data from complex models, and the fact that this cost often depends on parameter values. We therefore propose \textit{cost-aware SBI methods} which can significantly reduce the cost of existing sampling-based SBI methods, such as neural SBI and approximate Bayesian computation. This is achieved through a combination of rejection and self-normalised importance sampling, which significantly reduces the number of expensive simulations needed. Our approach is studied extensively on models from epidemiology to telecommunications engineering, where we obtain significant reductions in the overall cost of inference.
The Fundamental Dilemma of Bayesian Active Meta-learning
Oct 23, 2023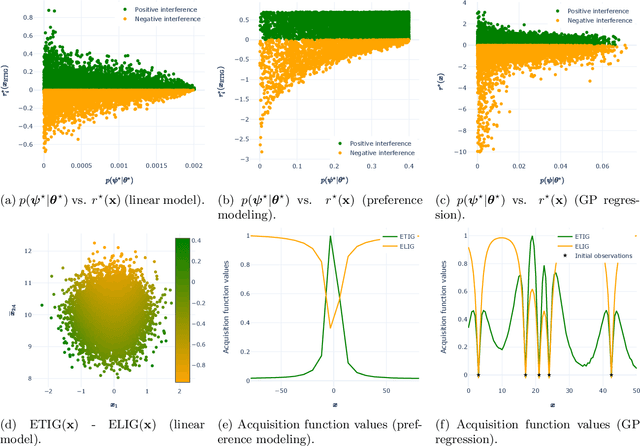
Abstract:Many applications involve estimation of parameters that generalize across multiple diverse, but related, data-scarce task environments. Bayesian active meta-learning, a form of sequential optimal experimental design, provides a framework for solving such problems. The active meta-learner's goal is to gain transferable knowledge (estimate the transferable parameters) in the presence of idiosyncratic characteristics of the current task (task-specific parameters). We show that in such a setting, greedy pursuit of this goal can actually hurt estimation of the transferable parameters (induce so-called negative transfer). The learner faces a dilemma akin to but distinct from the exploration--exploitation dilemma: should they spend their acquisition budget pursuing transferable knowledge, or identifying the current task-specific parameters? We show theoretically that some tasks pose an inevitable and arbitrarily large threat of negative transfer, and that task identification is critical to reducing this threat. Our results generalize to analysis of prior misspecification over nuisance parameters. Finally, we empirically illustrate circumstances that lead to negative transfer.
Learning Robust Statistics for Simulation-based Inference under Model Misspecification
May 25, 2023



Abstract:Simulation-based inference (SBI) methods such as approximate Bayesian computation (ABC), synthetic likelihood, and neural posterior estimation (NPE) rely on simulating statistics to infer parameters of intractable likelihood models. However, such methods are known to yield untrustworthy and misleading inference outcomes under model misspecification, thus hindering their widespread applicability. In this work, we propose the first general approach to handle model misspecification that works across different classes of SBI methods. Leveraging the fact that the choice of statistics determines the degree of misspecification in SBI, we introduce a regularized loss function that penalises those statistics that increase the mismatch between the data and the model. Taking NPE and ABC as use cases, we demonstrate the superior performance of our method on high-dimensional time-series models that are artificially misspecified. We also apply our method to real data from the field of radio propagation where the model is known to be misspecified. We show empirically that the method yields robust inference in misspecified scenarios, whilst still being accurate when the model is well-specified.
Cost-aware learning of relevant contextual variables within Bayesian optimization
May 24, 2023

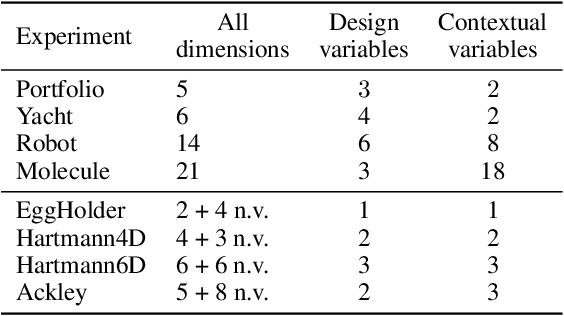

Abstract:Contextual Bayesian Optimization (CBO) is a powerful framework for optimizing black-box, expensive-to-evaluate functions with respect to design variables, while simultaneously efficiently integrating relevant contextual information regarding the environment, such as experimental conditions. However, in many practical scenarios, the relevance of contextual variables is not necessarily known beforehand. Moreover, the contextual variables can sometimes be optimized themselves, a setting that current CBO algorithms do not take into account. Optimizing contextual variables may be costly, which raises the question of determining a minimal relevant subset. In this paper, we frame this problem as a cost-aware model selection BO task and address it using a novel method, Sensitivity-Analysis-Driven Contextual BO (SADCBO). We learn the relevance of context variables by sensitivity analysis of the posterior surrogate model at specific input points, whilst minimizing the cost of optimization by leveraging recent developments on early stopping for BO. We empirically evaluate our proposed SADCBO against alternatives on synthetic experiments together with extensive ablation studies, and demonstrate a consistent improvement across examples.
Optimally-Weighted Estimators of the Maximum Mean Discrepancy for Likelihood-Free Inference
Jan 30, 2023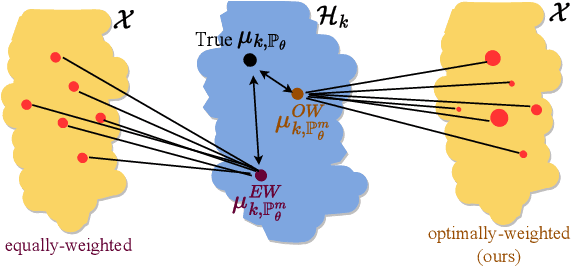

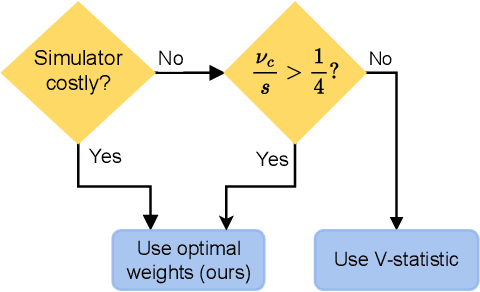
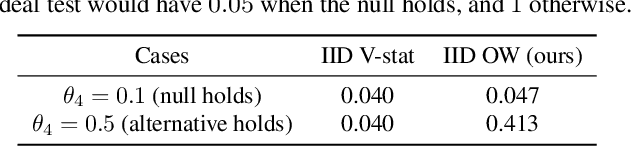
Abstract:Likelihood-free inference methods typically make use of a distance between simulated and real data. A common example is the maximum mean discrepancy (MMD), which has previously been used for approximate Bayesian computation, minimum distance estimation, generalised Bayesian inference, and within the nonparametric learning framework. The MMD is commonly estimated at a root-$m$ rate, where $m$ is the number of simulated samples. This can lead to significant computational challenges since a large $m$ is required to obtain an accurate estimate, which is crucial for parameter estimation. In this paper, we propose a novel estimator for the MMD with significantly improved sample complexity. The estimator is particularly well suited for computationally expensive smooth simulators with low- to mid-dimensional inputs. This claim is supported through both theoretical results and an extensive simulation study on benchmark simulators.
Approximate Bayesian Computation with Domain Expert in the Loop
Jan 28, 2022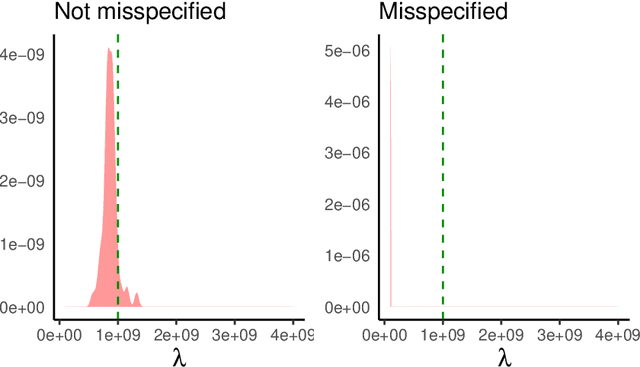

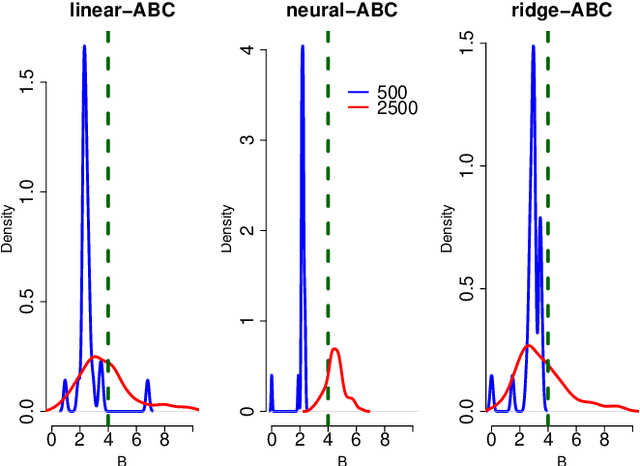

Abstract:Approximate Bayesian computation (ABC) is a popular likelihood-free inference method for models with intractable likelihood functions. As ABC methods usually rely on comparing summary statistics of observed and simulated data, the choice of the statistics is crucial. This choice involves a trade-off between loss of information and dimensionality reduction, and is often determined based on domain knowledge. However, handcrafting and selecting suitable statistics is a laborious task involving multiple trial-and-error steps. In this work, we introduce an active learning method for ABC statistics selection which reduces the domain expert's work considerably. By involving the experts, we are able to handle misspecified models, unlike the existing dimension reduction methods. Moreover, empirical results show better posterior estimates than with existing methods, when the simulation budget is limited.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge