Sabina J. Sloman
Robust Experimental Design via Generalised Bayesian Inference
Nov 10, 2025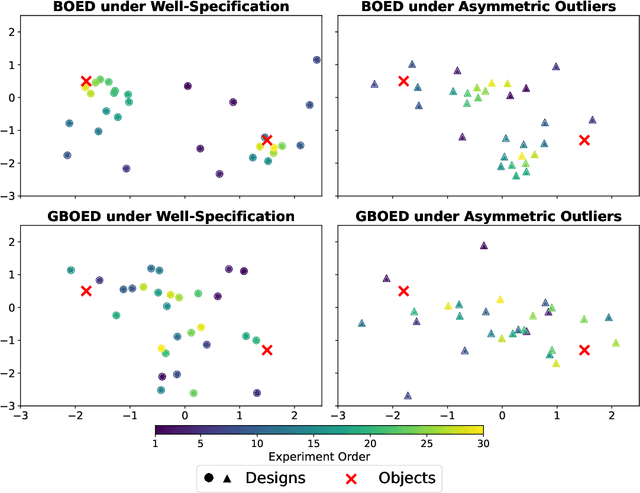
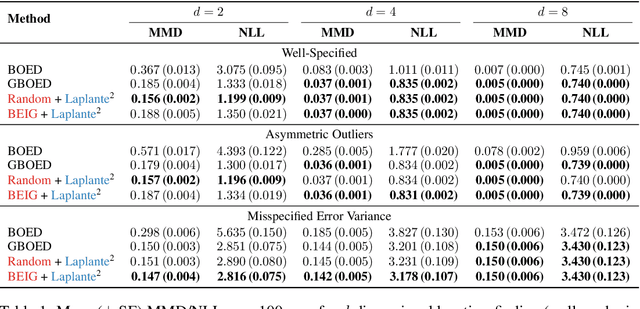
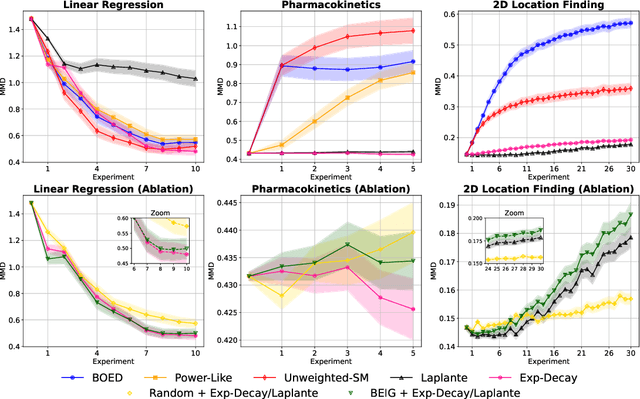
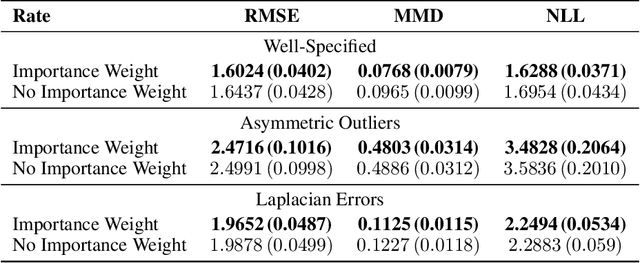
Abstract:Bayesian optimal experimental design is a principled framework for conducting experiments that leverages Bayesian inference to quantify how much information one can expect to gain from selecting a certain design. However, accurate Bayesian inference relies on the assumption that one's statistical model of the data-generating process is correctly specified. If this assumption is violated, Bayesian methods can lead to poor inference and estimates of information gain. Generalised Bayesian (or Gibbs) inference is a more robust probabilistic inference framework that replaces the likelihood in the Bayesian update by a suitable loss function. In this work, we present Generalised Bayesian Optimal Experimental Design (GBOED), an extension of Gibbs inference to the experimental design setting which achieves robustness in both design and inference. Using an extended information-theoretic framework, we derive a new acquisition function, the Gibbs expected information gain (Gibbs EIG). Our empirical results demonstrate that GBOED enhances robustness to outliers and incorrect assumptions about the outcome noise distribution.
Generalization Analysis for Bayesian Optimal Experiment Design under Model Misspecification
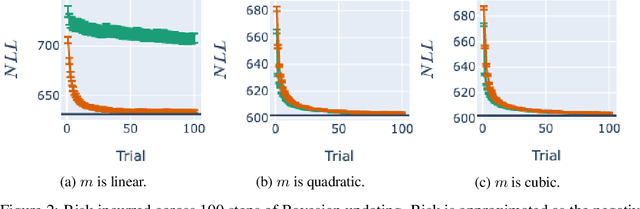
Jun 09, 2025Abstract:In many settings in science and industry, such as drug discovery and clinical trials, a central challenge is designing experiments under time and budget constraints. Bayesian Optimal Experimental Design (BOED) is a paradigm to pick maximally informative designs that has been increasingly applied to such problems. During training, BOED selects inputs according to a pre-determined acquisition criterion. During testing, the model learned during training encounters a naturally occurring distribution of test samples. This leads to an instance of covariate shift, where the train and test samples are drawn from different distributions. Prior work has shown that in the presence of model misspecification, covariate shift amplifies generalization error. Our first contribution is to provide a mathematical decomposition of generalization error that reveals key contributors to generalization error in the presence of model misspecification. We show that generalization error under misspecification is the result of, in addition to covariate shift, a phenomenon we term error (de-)amplification which has not been identified or studied in prior work. Our second contribution is to provide a detailed empirical analysis to show that methods that result in representative and de-amplifying training data increase generalization performance. Our third contribution is to develop a novel acquisition function that mitigates the effects of model misspecification by including a term for representativeness and implicitly inducing de-amplification. Our experimental results demonstrate that our method outperforms traditional BOED in the presence of misspecification.
Epistemic Errors of Imperfect Multitask Learners When Distributions Shift
May 29, 2025Abstract:When data are noisy, a statistical learner's goal is to resolve epistemic uncertainty about the data it will encounter at test-time, i.e., to identify the distribution of test (target) data. Many real-world learning settings introduce sources of epistemic uncertainty that can not be resolved on the basis of training (source) data alone: The source data may arise from multiple tasks (multitask learning), the target data may differ systematically from the source data tasks (distribution shift), and/or the learner may not arrive at an accurate characterization of the source data (imperfect learning). We introduce a principled definition of epistemic error, and provide a generic, decompositional epistemic error bound. Our error bound is the first to (i) consider epistemic error specifically, (ii) accommodate all the sources of epistemic uncertainty above, and (iii) separately attribute the error to each of multiple aspects of the learning procedure and environment. As corollaries of the generic result, we provide (i) epistemic error bounds specialized to the settings of Bayesian transfer learning and distribution shift within $\epsilon$-neighborhoods, and (ii) a set of corresponding generalization bounds. Finally, we provide a novel definition of negative transfer, and validate its insights in a synthetic experimental setting.
Proxy-informed Bayesian transfer learning with unknown sources
Nov 05, 2024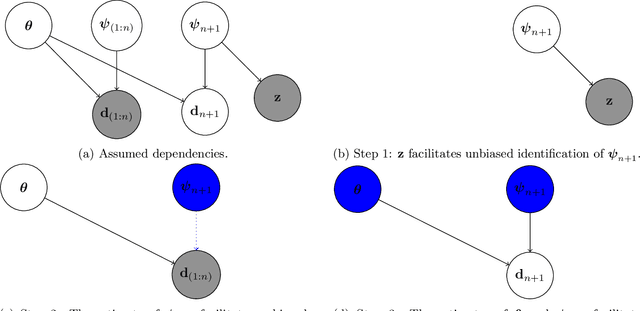
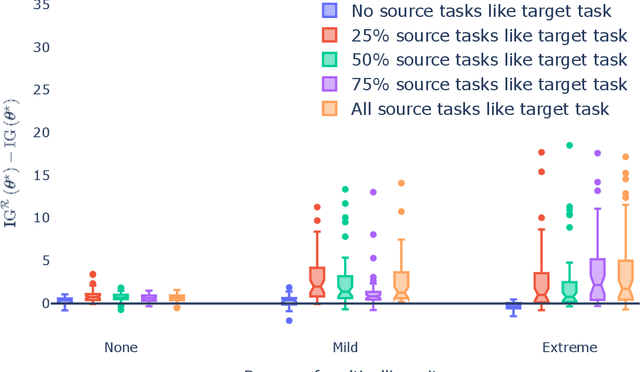
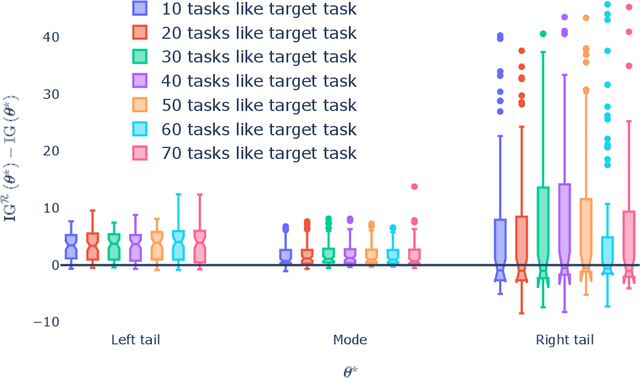
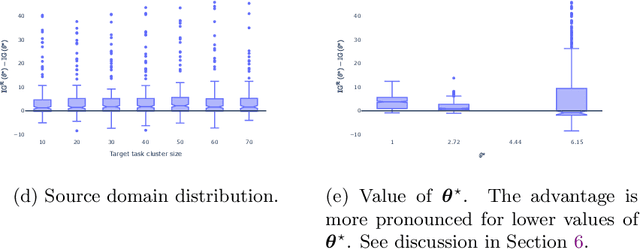
Abstract:Generalization outside the scope of one's training data requires leveraging prior knowledge about the effects that transfer, and the effects that don't, between different data sources. Bayesian transfer learning is a principled paradigm for specifying this knowledge, and refining it on the basis of data from the source (training) and target (prediction) tasks. We address the challenging transfer learning setting where the learner (i) cannot fine-tune in the target task, and (ii) does not know which source data points correspond to the same task (i.e., the data sources are unknown). We propose a proxy-informed robust method for probabilistic transfer learning (PROMPT), which provides a posterior predictive estimate tailored to the structure of the target task, without requiring the learner have access to any outcome information from the target task. Instead, PROMPT relies on the availability of proxy information. PROMPT uses the same proxy information for two purposes: (i) estimation of effects specific to the target task, and (ii) construction of a robust reweighting of the source data for estimation of effects that transfer between tasks. We provide theoretical results on the effect of this reweighting on the risk of negative transfer, and demonstrate application of PROMPT in two synthetic settings.
One system for learning and remembering episodes and rules
Jul 08, 2024
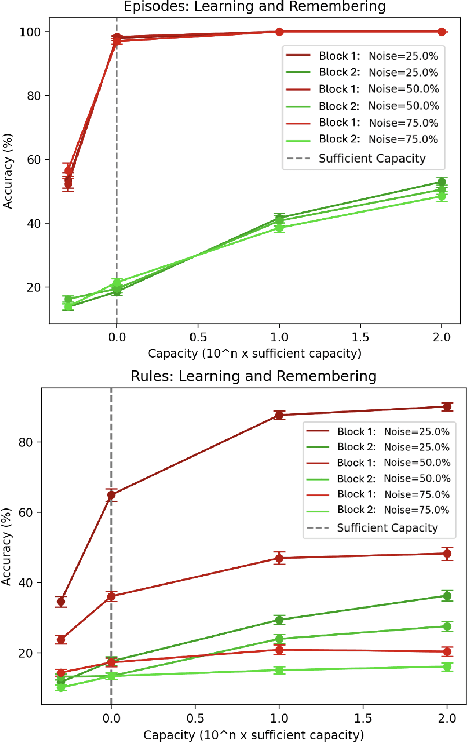
Abstract:Humans can learn individual episodes and generalizable rules and also successfully retain both kinds of acquired knowledge over time. In the cognitive science literature, (1) learning individual episodes and rules and (2) learning and remembering are often both conceptualized as competing processes that necessitate separate, complementary learning systems. Inspired by recent research in statistical learning, we challenge these trade-offs, hypothesizing that they arise from capacity limitations rather than from the inherent incompatibility of the underlying cognitive processes. Using an associative learning task, we show that one system with excess representational capacity can learn and remember both episodes and rules.
The Fundamental Dilemma of Bayesian Active Meta-learning
Oct 23, 2023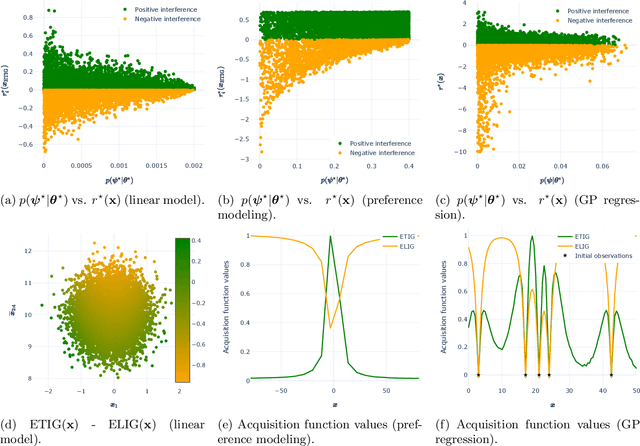
Abstract:Many applications involve estimation of parameters that generalize across multiple diverse, but related, data-scarce task environments. Bayesian active meta-learning, a form of sequential optimal experimental design, provides a framework for solving such problems. The active meta-learner's goal is to gain transferable knowledge (estimate the transferable parameters) in the presence of idiosyncratic characteristics of the current task (task-specific parameters). We show that in such a setting, greedy pursuit of this goal can actually hurt estimation of the transferable parameters (induce so-called negative transfer). The learner faces a dilemma akin to but distinct from the exploration--exploitation dilemma: should they spend their acquisition budget pursuing transferable knowledge, or identifying the current task-specific parameters? We show theoretically that some tasks pose an inevitable and arbitrarily large threat of negative transfer, and that task identification is critical to reducing this threat. Our results generalize to analysis of prior misspecification over nuisance parameters. Finally, we empirically illustrate circumstances that lead to negative transfer.
Characterizing the robustness of Bayesian adaptive experimental designs to active learning bias
May 27, 2022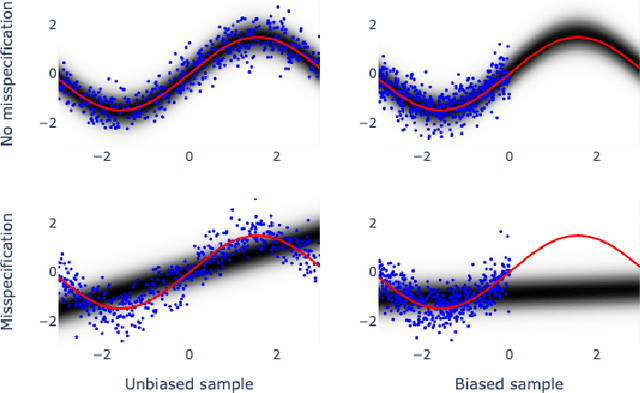
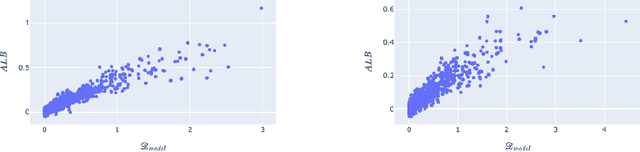
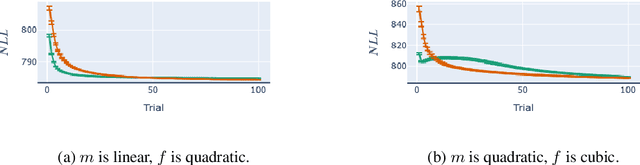
Abstract:Bayesian adaptive experimental design is a form of active learning, which chooses samples to maximize the information they give about uncertain parameters. Prior work has shown that other forms of active learning can suffer from active learning bias, where unrepresentative sampling leads to inconsistent parameter estimates. We show that active learning bias can also afflict Bayesian adaptive experimental design, depending on model misspecification. We develop an information-theoretic measure of misspecification, and show that worse misspecification implies more severe active learning bias. At the same time, model classes incorporating more "noise" - i.e., specifying higher inherent variance in observations - suffer less from active learning bias, because their predictive distributions are likely to overlap more with the true distribution. Finally, we show how these insights apply to a (simulated) preference learning experiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge