Characterizing the robustness of Bayesian adaptive experimental designs to active learning bias
Paper and Code
May 27, 2022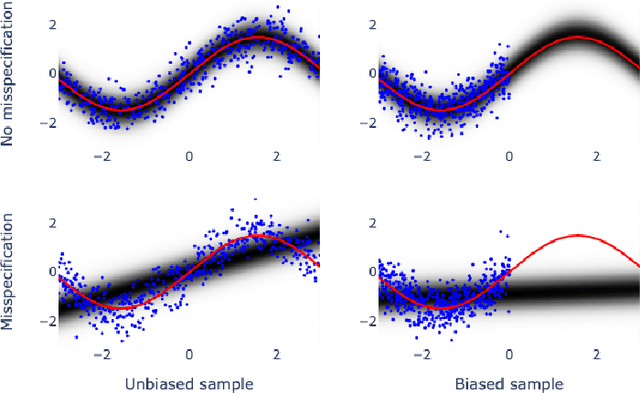
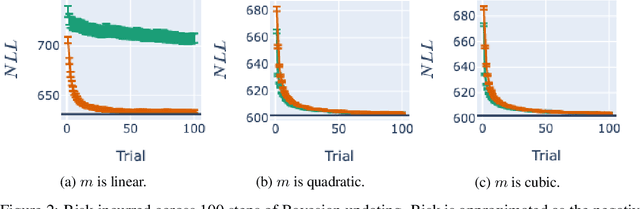
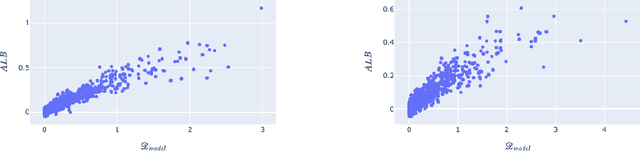
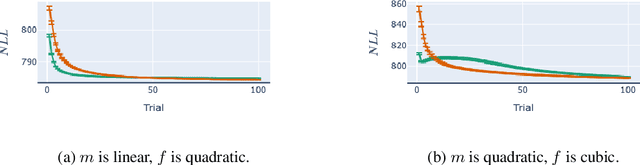
Bayesian adaptive experimental design is a form of active learning, which chooses samples to maximize the information they give about uncertain parameters. Prior work has shown that other forms of active learning can suffer from active learning bias, where unrepresentative sampling leads to inconsistent parameter estimates. We show that active learning bias can also afflict Bayesian adaptive experimental design, depending on model misspecification. We develop an information-theoretic measure of misspecification, and show that worse misspecification implies more severe active learning bias. At the same time, model classes incorporating more "noise" - i.e., specifying higher inherent variance in observations - suffer less from active learning bias, because their predictive distributions are likely to overlap more with the true distribution. Finally, we show how these insights apply to a (simulated) preference learning experiment.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge