Characterizing the robustness of Bayesian adaptive experimental designs to active learning bias

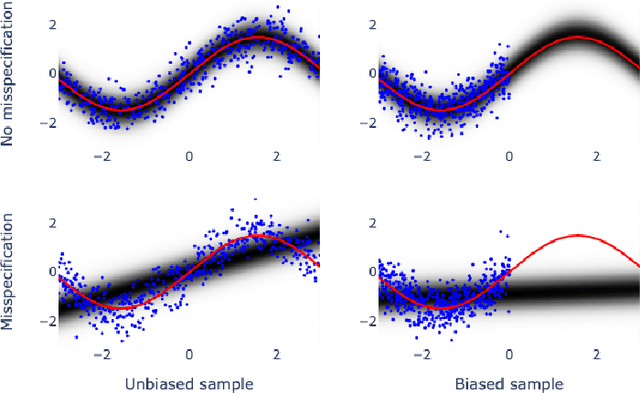
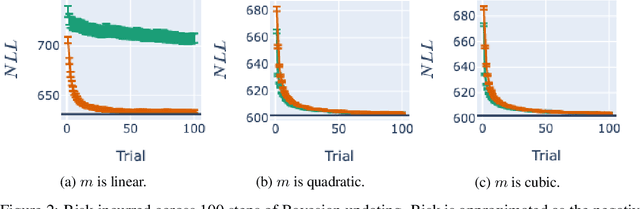
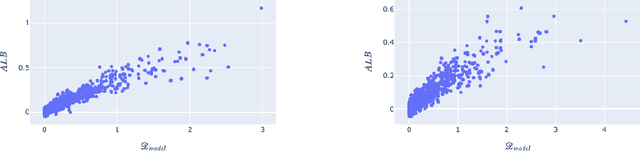
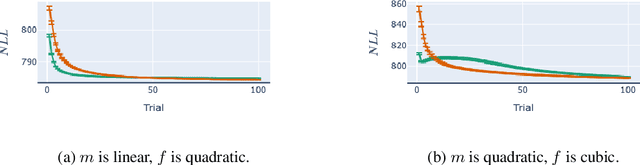
Bayesian adaptive experimental design is a form of active learning, which chooses samples to maximize the information they give about uncertain parameters. Prior work has shown that other forms of active learning can suffer from active learning bias, where unrepresentative sampling leads to inconsistent parameter estimates. We show that active learning bias can also afflict Bayesian adaptive experimental design, depending on model misspecification. We develop an information-theoretic measure of misspecification, and show that worse misspecification implies more severe active learning bias. At the same time, model classes incorporating more "noise" - i.e., specifying higher inherent variance in observations - suffer less from active learning bias, because their predictive distributions are likely to overlap more with the true distribution. Finally, we show how these insights apply to a (simulated) preference learning experiment.

Rademacher complexity of stationary sequences

We show how to control the generalization error of time series models wherein past values of the outcome are used to predict future values. The results are based on a generalization of standard i.i.d. concentration inequalities to dependent data without the mixing assumptions common in the time series setting. Our proof and the result are simpler than previous analyses with dependent data or stochastic adversaries which use sequential Rademacher complexities rather than the expected Rademacher complexity for i.i.d. processes. We also derive empirical Rademacher results without mixing assumptions resulting in fully calculable upper bounds.

The LICORS Cabinet: Nonparametric Algorithms for Spatio-temporal Prediction

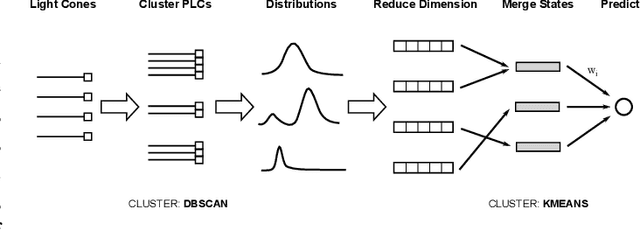
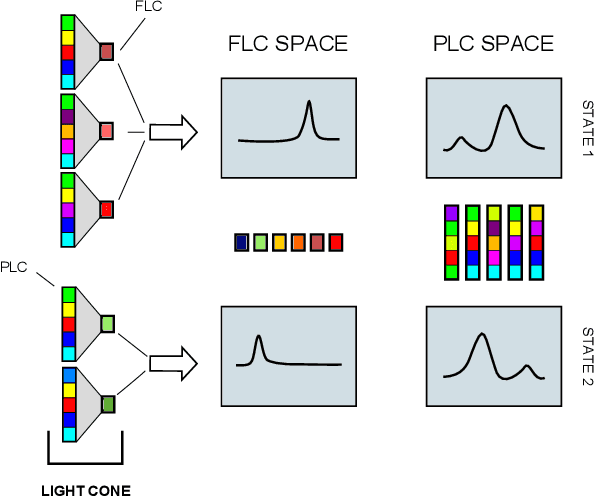
Spatio-temporal data is intrinsically high dimensional, so unsupervised modeling is only feasible if we can exploit structure in the process. When the dynamics are local in both space and time, this structure can be exploited by splitting the global field into many lower-dimensional "light cones". We review light cone decompositions for predictive state reconstruction, introducing three simple light cone algorithms. These methods allow for tractable inference of spatio-temporal data, such as full-frame video. The algorithms make few assumptions on the underlying process yet have good predictive performance and can provide distributions over spatio-temporal data, enabling sophisticated probabilistic inference.

Nonparametric risk bounds for time-series forecasting

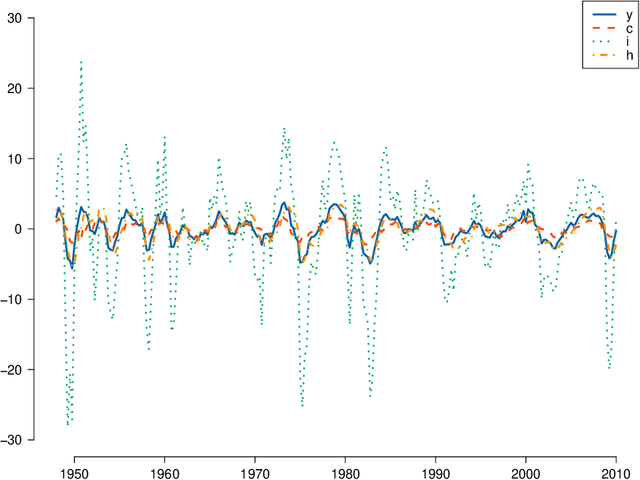
We derive generalization error bounds for traditional time-series forecasting models. Our results hold for many standard forecasting tools including autoregressive models, moving average models, and, more generally, linear state-space models. These non-asymptotic bounds need only weak assumptions on the data-generating process, yet allow forecasters to select among competing models and to guarantee, with high probability, that their chosen model will perform well. We motivate our techniques with and apply them to standard economic and financial forecasting tools---a GARCH model for predicting equity volatility and a dynamic stochastic general equilibrium model (DSGE), the standard tool in macroeconomic forecasting. We demonstrate in particular how our techniques can aid forecasters and policy makers in choosing models which behave well under uncertainty and mis-specification.

Predictive PAC Learning and Process Decompositions

We informally call a stochastic process learnable if it admits a generalization error approaching zero in probability for any concept class with finite VC-dimension (IID processes are the simplest example). A mixture of learnable processes need not be learnable itself, and certainly its generalization error need not decay at the same rate. In this paper, we argue that it is natural in predictive PAC to condition not on the past observations but on the mixture component of the sample path. This definition not only matches what a realistic learner might demand, but also allows us to sidestep several otherwise grave problems in learning from dependent data. In particular, we give a novel PAC generalization bound for mixtures of learnable processes with a generalization error that is not worse than that of each mixture component. We also provide a characterization of mixtures of absolutely regular ($\beta$-mixing) processes, of independent probability-theoretic interest.

Model Selection for Degree-corrected Block Models

The proliferation of models for networks raises challenging problems of model selection: the data are sparse and globally dependent, and models are typically high-dimensional and have large numbers of latent variables. Together, these issues mean that the usual model-selection criteria do not work properly for networks. We illustrate these challenges, and show one way to resolve them, by considering the key network-analysis problem of dividing a graph into communities or blocks of nodes with homogeneous patterns of links to the rest of the network. The standard tool for doing this is the stochastic block model, under which the probability of a link between two nodes is a function solely of the blocks to which they belong. This imposes a homogeneous degree distribution within each block; this can be unrealistic, so degree-corrected block models add a parameter for each node, modulating its over-all degree. The choice between ordinary and degree-corrected block models matters because they make very different inferences about communities. We present the first principled and tractable approach to model selection between standard and degree-corrected block models, based on new large-graph asymptotics for the distribution of log-likelihood ratios under the stochastic block model, finding substantial departures from classical results for sparse graphs. We also develop linear-time approximations for log-likelihoods under both the stochastic block model and the degree-corrected model, using belief propagation. Applications to simulated and real networks show excellent agreement with our approximations. Our results thus both solve the practical problem of deciding on degree correction, and point to a general approach to model selection in network analysis.

Mixed LICORS: A Nonparametric Algorithm for Predictive State Reconstruction

We introduce 'mixed LICORS', an algorithm for learning nonlinear, high-dimensional dynamics from spatio-temporal data, suitable for both prediction and simulation. Mixed LICORS extends the recent LICORS algorithm (Goerg and Shalizi, 2012) from hard clustering of predictive distributions to a non-parametric, EM-like soft clustering. This retains the asymptotic predictive optimality of LICORS, but, as we show in simulations, greatly improves out-of-sample forecasts with limited data. The new method is implemented in the publicly-available R package "LICORS" (http://cran.r-project.org/web/packages/LICORS/).

Estimated VC dimension for risk bounds

Vapnik-Chervonenkis (VC) dimension is a fundamental measure of the generalization capacity of learning algorithms. However, apart from a few special cases, it is hard or impossible to calculate analytically. Vapnik et al. [10] proposed a technique for estimating the VC dimension empirically. While their approach behaves well in simulations, it could not be used to bound the generalization risk of classifiers, because there were no bounds for the estimation error of the VC dimension itself. We rectify this omission, providing high probability concentration results for the proposed estimator and deriving corresponding generalization bounds.

Adapting to Non-stationarity with Growing Expert Ensembles

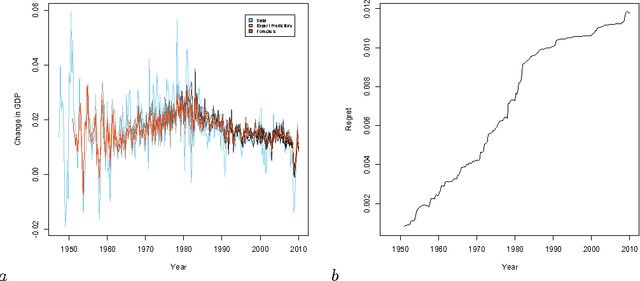
When dealing with time series with complex non-stationarities, low retrospective regret on individual realizations is a more appropriate goal than low prospective risk in expectation. Online learning algorithms provide powerful guarantees of this form, and have often been proposed for use with non-stationary processes because of their ability to switch between different forecasters or ``experts''. However, existing methods assume that the set of experts whose forecasts are to be combined are all given at the start, which is not plausible when dealing with a genuinely historical or evolutionary system. We show how to modify the ``fixed shares'' algorithm for tracking the best expert to cope with a steadily growing set of experts, obtained by fitting new models to new data as it becomes available, and obtain regret bounds for the growing ensemble.

Generalization error bounds for stationary autoregressive models

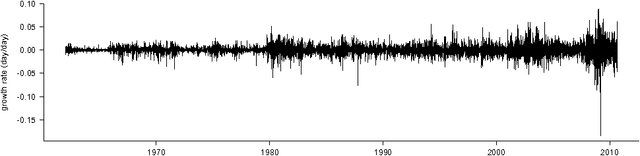
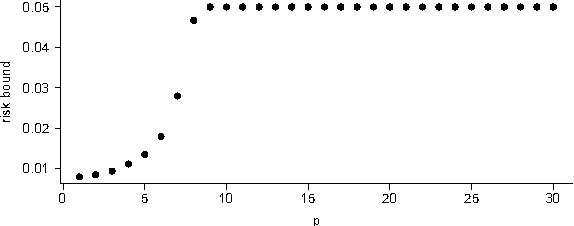
We derive generalization error bounds for stationary univariate autoregressive (AR) models. We show that imposing stationarity is enough to control the Gaussian complexity without further regularization. This lets us use structural risk minimization for model selection. We demonstrate our methods by predicting interest rate movements.