Rademacher complexity of stationary sequences

We show how to control the generalization error of time series models wherein past values of the outcome are used to predict future values. The results are based on a generalization of standard i.i.d. concentration inequalities to dependent data without the mixing assumptions common in the time series setting. Our proof and the result are simpler than previous analyses with dependent data or stochastic adversaries which use sequential Rademacher complexities rather than the expected Rademacher complexity for i.i.d. processes. We also derive empirical Rademacher results without mixing assumptions resulting in fully calculable upper bounds.

Nonparametric risk bounds for time-series forecasting

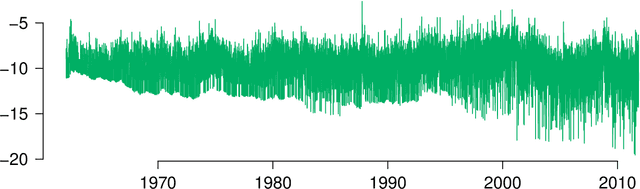
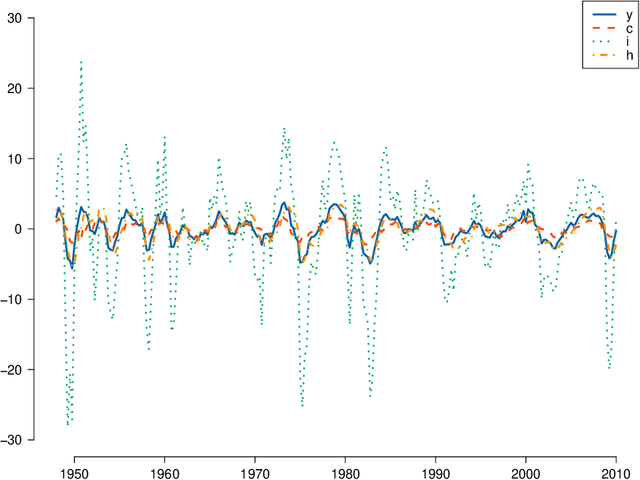
We derive generalization error bounds for traditional time-series forecasting models. Our results hold for many standard forecasting tools including autoregressive models, moving average models, and, more generally, linear state-space models. These non-asymptotic bounds need only weak assumptions on the data-generating process, yet allow forecasters to select among competing models and to guarantee, with high probability, that their chosen model will perform well. We motivate our techniques with and apply them to standard economic and financial forecasting tools---a GARCH model for predicting equity volatility and a dynamic stochastic general equilibrium model (DSGE), the standard tool in macroeconomic forecasting. We demonstrate in particular how our techniques can aid forecasters and policy makers in choosing models which behave well under uncertainty and mis-specification.

Risk-consistency of cross-validation with lasso-type procedures

The lasso and related sparsity inducing algorithms have been the target of substantial theoretical and applied research. Correspondingly, many results are known about their behavior for a fixed or optimally chosen tuning parameter specified up to unknown constants. In practice, however, this oracle tuning parameter is inaccessible so one must use the data to select one. Common statistical practice is to use a variant of cross-validation for this task. However, little is known about the theoretical properties of the resulting predictions with such data-dependent methods. We consider the high-dimensional setting with random design wherein the number of predictors $p$ grows with the number of observations $n$. Under typical assumptions on the data generating process, similar to those in the literature, we recover oracle rates up to a log factor when choosing the tuning parameter with cross-validation. Under weaker conditions, when the true model is not necessarily linear, we show that the lasso remains risk consistent relative to its linear oracle. We also generalize these results to the group lasso and square-root lasso and investigate the predictive and model selection performance of cross-validation via simulation.

Risk estimation for high-dimensional lasso regression

In high-dimensional estimation, analysts are faced with more parameters $p$ than available observations $n$, and asymptotic analysis of performance allows the ratio $p/n\rightarrow \infty$. This situation makes regularization both necessary and desirable in order for estimators to possess theoretical guarantees. However, the amount of regularization, often determined by one or more tuning parameters, is integral to achieving good performance. In practice, choosing the tuning parameter is done through resampling methods (e.g. cross-validation), generalized information criteria, or reformulating the optimization problem (e.g. square-root lasso or scaled sparse regression). Each of these techniques comes with varying levels of theoretical guarantee for the low- or high-dimensional regimes. However, there are some notable deficiencies in the literature. The theory, and sometimes practice, of many methods relies on either the knowledge or estimation of the variance parameter, which is difficult to estimate in high dimensions. In this paper, we provide theoretical intuition suggesting that some previously proposed approaches based on information criteria work poorly in high dimensions. We introduce a suite of new risk estimators leveraging the burgeoning literature on high-dimensional variance estimation. Finally, we compare our proposal to many existing methods for choosing the tuning parameters for lasso regression by providing an extensive simulation to examine their finite sample performance. We find that our new estimators perform quite well, often better than the existing approaches across a wide range of simulation conditions and evaluation criteria.

On the Nyström and Column-Sampling Methods for the Approximate Principal Components Analysis of Large Data Sets

In this paper we analyze approximate methods for undertaking a principal components analysis (PCA) on large data sets. PCA is a classical dimension reduction method that involves the projection of the data onto the subspace spanned by the leading eigenvectors of the covariance matrix. This projection can be used either for exploratory purposes or as an input for further analysis, e.g. regression. If the data have billions of entries or more, the computational and storage requirements for saving and manipulating the design matrix in fast memory is prohibitive. Recently, the Nystr\"om and column-sampling methods have appeared in the numerical linear algebra community for the randomized approximation of the singular value decomposition of large matrices. However, their utility for statistical applications remains unclear. We compare these approximations theoretically by bounding the distance between the induced subspaces and the desired, but computationally infeasible, PCA subspace. Additionally we show empirically, through simulations and a real data example involving a corpus of emails, the trade-off of approximation accuracy and computational complexity.

Estimated VC dimension for risk bounds

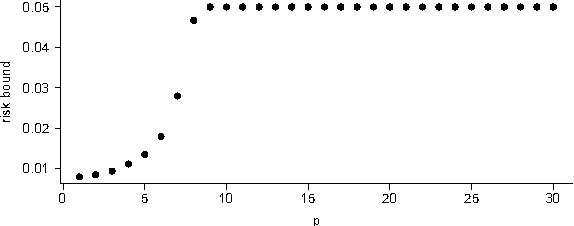
Vapnik-Chervonenkis (VC) dimension is a fundamental measure of the generalization capacity of learning algorithms. However, apart from a few special cases, it is hard or impossible to calculate analytically. Vapnik et al. [10] proposed a technique for estimating the VC dimension empirically. While their approach behaves well in simulations, it could not be used to bound the generalization risk of classifiers, because there were no bounds for the estimation error of the VC dimension itself. We rectify this omission, providing high probability concentration results for the proposed estimator and deriving corresponding generalization bounds.

Spectral approximations in machine learning

In many areas of machine learning, it becomes necessary to find the eigenvector decompositions of large matrices. We discuss two methods for reducing the computational burden of spectral decompositions: the more venerable Nystom extension and a newly introduced algorithm based on random projections. Previous work has centered on the ability to reconstruct the original matrix. We argue that a more interesting and relevant comparison is their relative performance in clustering and classification tasks using the approximate eigenvectors as features. We demonstrate that performance is task specific and depends on the rank of the approximation.

Generalization error bounds for stationary autoregressive models

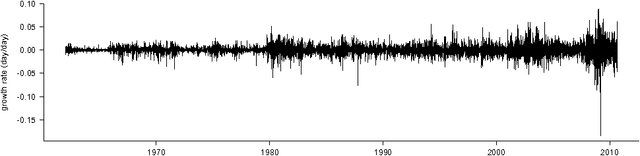
We derive generalization error bounds for stationary univariate autoregressive (AR) models. We show that imposing stationarity is enough to control the Gaussian complexity without further regularization. This lets us use structural risk minimization for model selection. We demonstrate our methods by predicting interest rate movements.

Estimating $β$-mixing coefficients

The literature on statistical learning for time series assumes the asymptotic independence or ``mixing' of the data-generating process. These mixing assumptions are never tested, nor are there methods for estimating mixing rates from data. We give an estimator for the $\beta$-mixing rate based on a single stationary sample path and show it is $L_1$-risk consistent.