Nonparametric risk bounds for time-series forecasting

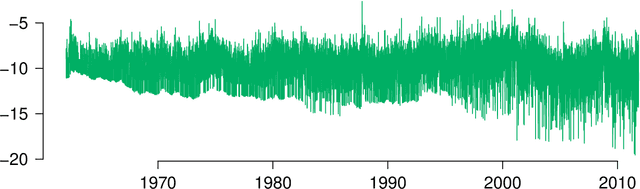
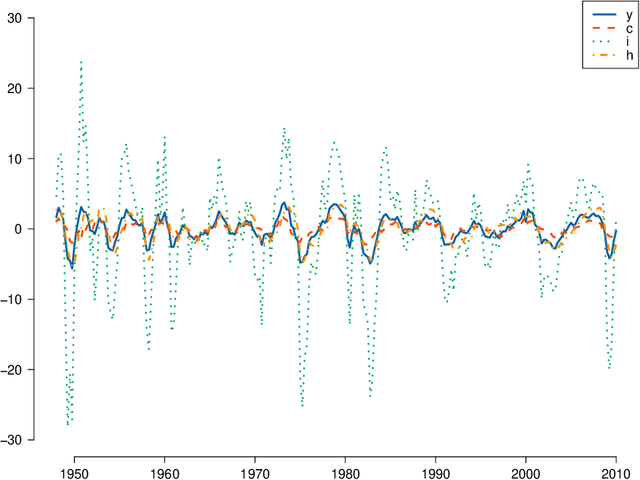
We derive generalization error bounds for traditional time-series forecasting models. Our results hold for many standard forecasting tools including autoregressive models, moving average models, and, more generally, linear state-space models. These non-asymptotic bounds need only weak assumptions on the data-generating process, yet allow forecasters to select among competing models and to guarantee, with high probability, that their chosen model will perform well. We motivate our techniques with and apply them to standard economic and financial forecasting tools---a GARCH model for predicting equity volatility and a dynamic stochastic general equilibrium model (DSGE), the standard tool in macroeconomic forecasting. We demonstrate in particular how our techniques can aid forecasters and policy makers in choosing models which behave well under uncertainty and mis-specification.

Estimated VC dimension for risk bounds

Vapnik-Chervonenkis (VC) dimension is a fundamental measure of the generalization capacity of learning algorithms. However, apart from a few special cases, it is hard or impossible to calculate analytically. Vapnik et al. [10] proposed a technique for estimating the VC dimension empirically. While their approach behaves well in simulations, it could not be used to bound the generalization risk of classifiers, because there were no bounds for the estimation error of the VC dimension itself. We rectify this omission, providing high probability concentration results for the proposed estimator and deriving corresponding generalization bounds.

Generalization error bounds for stationary autoregressive models

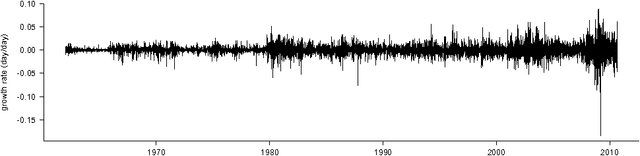
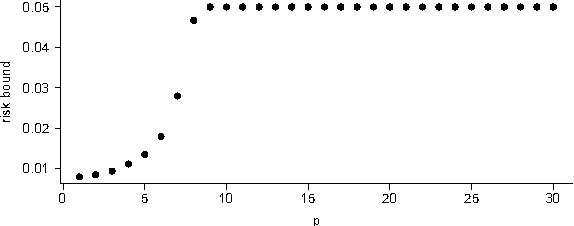
We derive generalization error bounds for stationary univariate autoregressive (AR) models. We show that imposing stationarity is enough to control the Gaussian complexity without further regularization. This lets us use structural risk minimization for model selection. We demonstrate our methods by predicting interest rate movements.

Estimating $β$-mixing coefficients

The literature on statistical learning for time series assumes the asymptotic independence or ``mixing' of the data-generating process. These mixing assumptions are never tested, nor are there methods for estimating mixing rates from data. We give an estimator for the $\beta$-mixing rate based on a single stationary sample path and show it is $L_1$-risk consistent.