Tensor cumulants for statistical inference on invariant distributions

Many problems in high-dimensional statistics appear to have a statistical-computational gap: a range of values of the signal-to-noise ratio where inference is information-theoretically possible, but (conjecturally) computationally intractable. A canonical such problem is Tensor PCA, where we observe a tensor $Y$ consisting of a rank-one signal plus Gaussian noise. Multiple lines of work suggest that Tensor PCA becomes computationally hard at a critical value of the signal's magnitude. In particular, below this transition, no low-degree polynomial algorithm can detect the signal with high probability; conversely, various spectral algorithms are known to succeed above this transition. We unify and extend this work by considering tensor networks, orthogonally invariant polynomials where multiple copies of $Y$ are "contracted" to produce scalars, vectors, matrices, or other tensors. We define a new set of objects, tensor cumulants, which provide an explicit, near-orthogonal basis for invariant polynomials of a given degree. This basis lets us unify and strengthen previous results on low-degree hardness, giving a combinatorial explanation of the hardness transition and of a continuum of subexponential-time algorithms that work below it, and proving tight lower bounds against low-degree polynomials for recovering rather than just detecting the signal. It also lets us analyze a new problem of distinguishing between different tensor ensembles, such as Wigner and Wishart tensors, establishing a sharp computational threshold and giving evidence of a new statistical-computational gap in the Central Limit Theorem for random tensors. Finally, we believe these cumulants are valuable mathematical objects in their own right: they generalize the free cumulants of free probability theory from matrices to tensors, and share many of their properties, including additivity under additive free convolution.

A model for efficient dynamical ranking in networks

We present a physics-inspired method for inferring dynamic rankings in directed temporal networks - networks in which each directed and timestamped edge reflects the outcome and timing of a pairwise interaction. The inferred ranking of each node is real-valued and varies in time as each new edge, encoding an outcome like a win or loss, raises or lowers the node's estimated strength or prestige, as is often observed in real scenarios including sequences of games, tournaments, or interactions in animal hierarchies. Our method works by solving a linear system of equations and requires only one parameter to be tuned. As a result, the corresponding algorithm is scalable and efficient. We test our method by evaluating its ability to predict interactions (edges' existence) and their outcomes (edges' directions) in a variety of applications, including both synthetic and real data. Our analysis shows that in many cases our method's performance is better than existing methods for predicting dynamic rankings and interaction outcomes.

Belief propagation for permutations, rankings, and partial orders

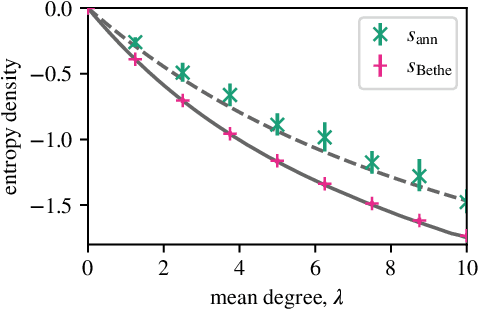
Many datasets give partial information about an ordering or ranking by indicating which team won a game, which item a user prefers, or who infected whom. We define a continuous spin system whose Gibbs distribution is the posterior distribution on permutations, given a probabilistic model of these interactions. Using the cavity method we derive a belief propagation algorithm that computes the marginal distribution of each node's position. In addition, the Bethe free energy lets us approximate the number of linear extensions of a partial order and perform model selection.

Improved Reconstruction of Random Geometric Graphs

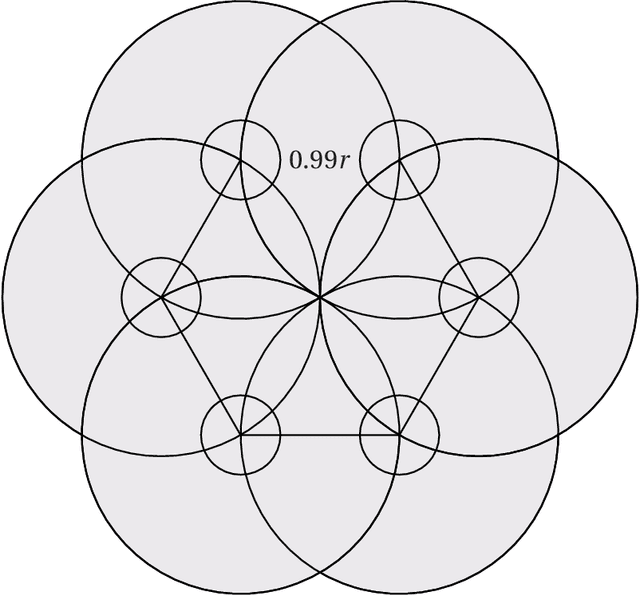
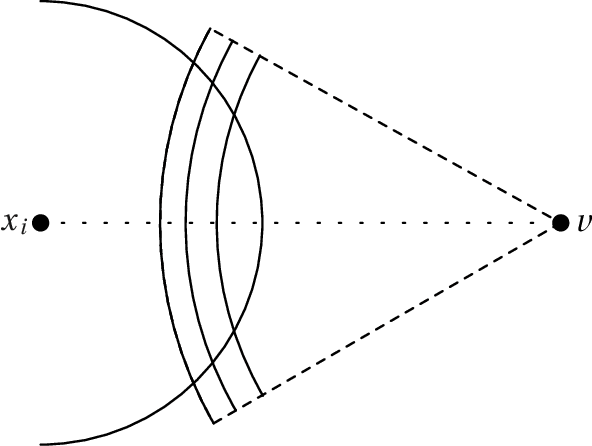
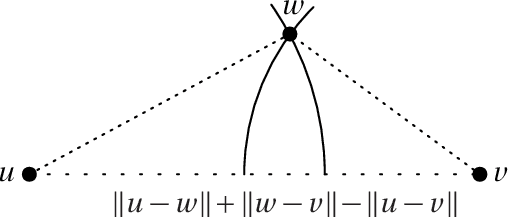
Embedding graphs in a geographical or latent space, i.e., inferring locations for vertices in Euclidean space or on a smooth submanifold, is a common task in network analysis, statistical inference, and graph visualization. We consider the classic model of random geometric graphs where $n$ points are scattered uniformly in a square of area $n$, and two points have an edge between them if and only if their Euclidean distance is less than $r$. The reconstruction problem then consists of inferring the vertex positions, up to symmetry, given only the adjacency matrix of the resulting graph. We give an algorithm that, if $r=n^\alpha$ for $\alpha > 0$, with high probability reconstructs the vertex positions with a maximum error of $O(n^\beta)$ where $\beta=1/2-(4/3)\alpha$, until $\alpha \ge 3/8$ where $\beta=0$ and the error becomes $O(\sqrt{\log n})$. This improves over earlier results, which were unable to reconstruct with error less than $r$. Our method estimates Euclidean distances using a hybrid of graph distances and short-range estimates based on the number of common neighbors. We sketch proofs that our results also apply on the surface of a sphere, and (with somewhat different exponents) in any fixed dimension.

The Planted Matching Problem: Phase Transitions and Exact Results

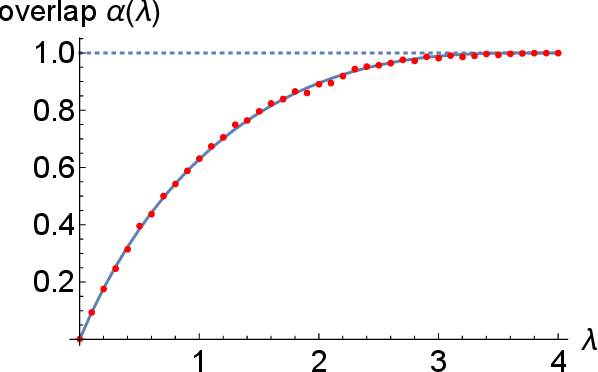
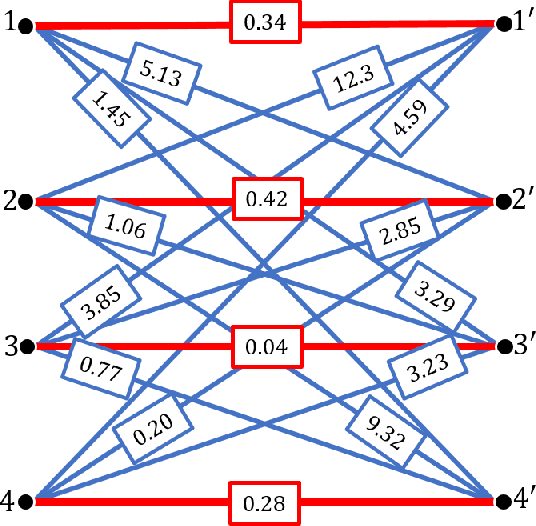
We study the problem of recovering a planted matching in randomly weighted complete bipartite graphs $K_{n,n}$. For some unknown perfect matching $M^*$, the weight of an edge is drawn from one distribution $P$ if $e \in M^*$ and another distribution $Q$ if $e \in M^*$. Our goal is to infer $M^*$, exactly or approximately, from the edge weights. In this paper we take $P=\exp(\lambda)$ and $Q=\exp(1/n)$, in which case the maximum-likelihood estimator of $M^*$ is the minimum-weight matching $M_{\min}$. We obtain precise results on the overlap between $M^*$ and $M_{\min}$, i.e., the fraction of edges they have in common. For $\lambda \ge 4$ we have almost-perfect recovery, with overlap $1-o(1)$ with high probability. For $\lambda < 4$ the expected overlap is an explicit function $\alpha(\lambda) < 1$: we compute it by generalizing Aldous' celebrated proof of M\'ezard and Parisi's $\zeta(2)$ conjecture for the un-planted model, using local weak convergence to relate $K_{n,n}$ to a type of weighted infinite tree, and then deriving a system of differential equations from a message-passing algorithm on this tree.

The Kikuchi Hierarchy and Tensor PCA

For the tensor PCA (principal component analysis) problem, we propose a new hierarchy of algorithms that are increasingly powerful yet require increasing runtime. Our hierarchy is analogous to the sum-of-squares (SOS) hierarchy but is instead inspired by statistical physics and related algorithms such as belief propagation and AMP (approximate message passing). Our level-$\ell$ algorithm can be thought of as a (linearized) message-passing algorithm that keeps track of $\ell$-wise dependencies among the hidden variables. Specifically, our algorithms are spectral methods based on the Kikuchi Hessian matrix, which generalizes the well-studied Bethe Hessian matrix to the higher-order Kikuchi free energies. It is known that AMP, the flagship algorithm of statistical physics, has substantially worse performance than SOS for tensor PCA. In this work we `redeem' the statistical physics approach by showing that our hierarchy gives a polynomial-time algorithm matching the performance of SOS. Our hierarchy also yields a continuum of subexponential-time algorithms, and we prove that these achieve the same (conjecturally optimal) tradeoff between runtime and statistical power as SOS. Our results hold for even-order tensors, and we conjecture that they also hold for odd-order tensors. Our methods suggest a new avenue for systematically obtaining optimal algorithms for Bayesian inference problems, and our results constitute a step toward unifying the statistical physics and sum-of-squares approaches to algorithm design.

Accurate and scalable social recommendation using mixed-membership stochastic block models

With ever-increasing amounts of online information available, modeling and predicting individual preferences-for books or articles, for example-is becoming more and more important. Good predictions enable us to improve advice to users, and obtain a better understanding of the socio-psychological processes that determine those preferences. We have developed a collaborative filtering model, with an associated scalable algorithm, that makes accurate predictions of individuals' preferences. Our approach is based on the explicit assumption that there are groups of individuals and of items, and that the preferences of an individual for an item are determined only by their group memberships. Importantly, we allow each individual and each item to belong simultaneously to mixtures of different groups and, unlike many popular approaches, such as matrix factorization, we do not assume implicitly or explicitly that individuals in each group prefer items in a single group of items. The resulting overlapping groups and the predicted preferences can be inferred with a expectation-maximization algorithm whose running time scales linearly (per iteration). Our approach enables us to predict individual preferences in large datasets, and is considerably more accurate than the current algorithms for such large datasets.

Detectability thresholds and optimal algorithms for community structure in dynamic networks

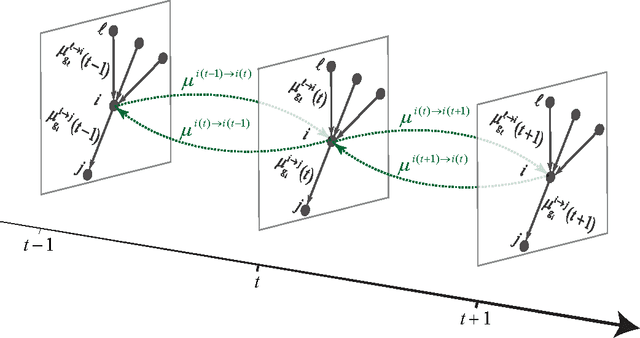
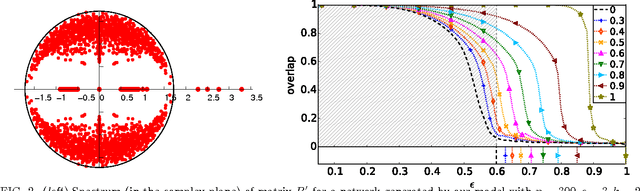
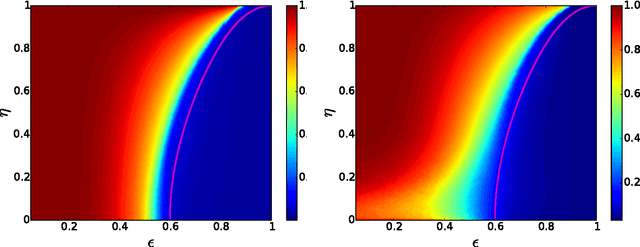
We study the fundamental limits on learning latent community structure in dynamic networks. Specifically, we study dynamic stochastic block models where nodes change their community membership over time, but where edges are generated independently at each time step. In this setting (which is a special case of several existing models), we are able to derive the detectability threshold exactly, as a function of the rate of change and the strength of the communities. Below this threshold, we claim that no algorithm can identify the communities better than chance. We then give two algorithms that are optimal in the sense that they succeed all the way down to this limit. The first uses belief propagation (BP), which gives asymptotically optimal accuracy, and the second is a fast spectral clustering algorithm, based on linearizing the BP equations. We verify our analytic and algorithmic results via numerical simulation, and close with a brief discussion of extensions and open questions.

On the universal structure of human lexical semantics

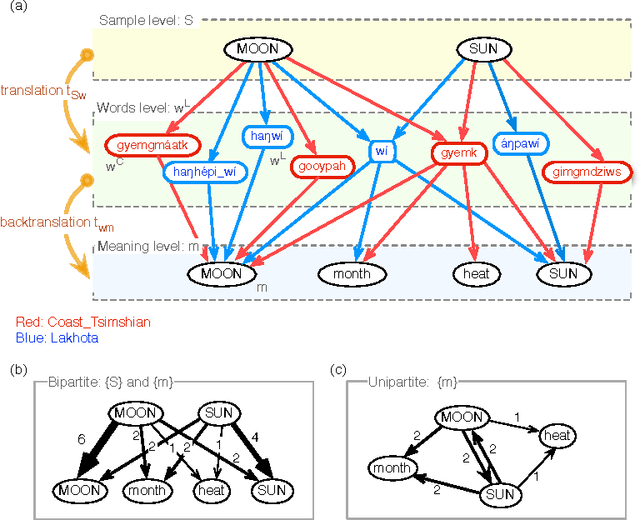
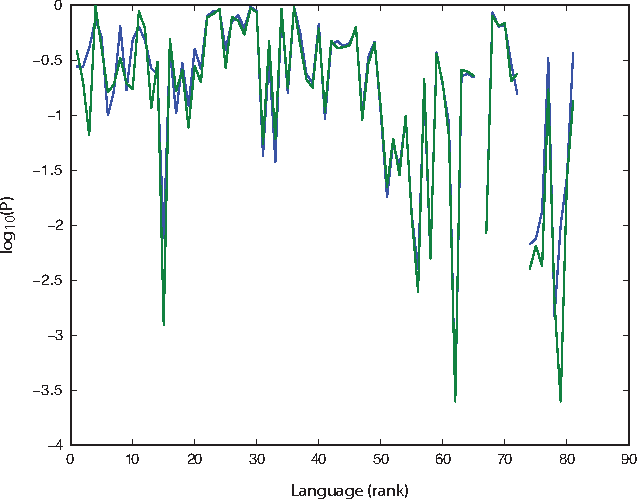
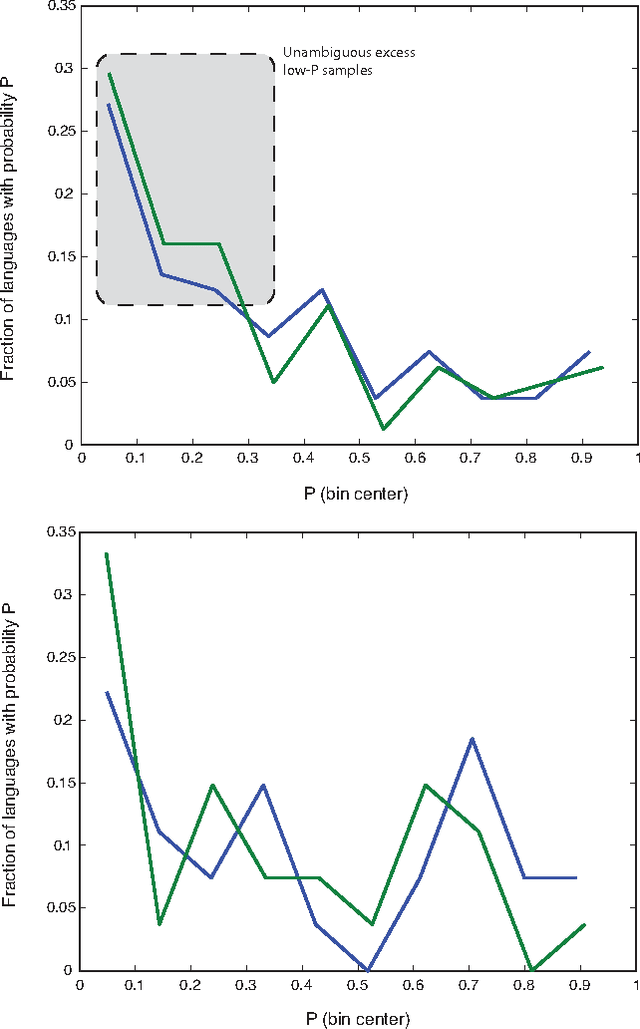
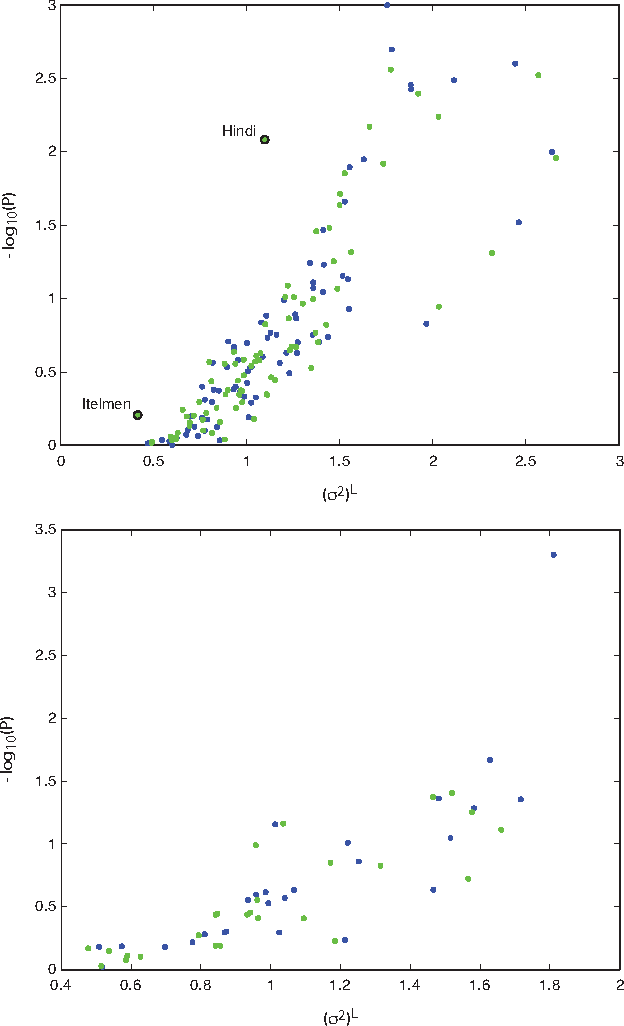
How universal is human conceptual structure? The way concepts are organized in the human brain may reflect distinct features of cultural, historical, and environmental background in addition to properties universal to human cognition. Semantics, or meaning expressed through language, provides direct access to the underlying conceptual structure, but meaning is notoriously difficult to measure, let alone parameterize. Here we provide an empirical measure of semantic proximity between concepts using cross-linguistic dictionaries. Across languages carefully selected from a phylogenetically and geographically stratified sample of genera, translations of words reveal cases where a particular language uses a single polysemous word to express concepts represented by distinct words in another. We use the frequency of polysemies linking two concepts as a measure of their semantic proximity, and represent the pattern of such linkages by a weighted network. This network is highly uneven and fragmented: certain concepts are far more prone to polysemy than others, and there emerge naturally interpretable clusters loosely connected to each other. Statistical analysis shows such structural properties are consistent across different language groups, largely independent of geography, environment, and literacy. It is therefore possible to conclude the conceptual structure connecting basic vocabulary studied is primarily due to universal features of human cognition and language use.

Scalable detection of statistically significant communities and hierarchies, using message-passing for modularity

Modularity is a popular measure of community structure. However, maximizing the modularity can lead to many competing partitions, with almost the same modularity, that are poorly correlated with each other. It can also produce illusory "communities" in random graphs where none exist. We address this problem by using the modularity as a Hamiltonian at finite temperature, and using an efficient Belief Propagation algorithm to obtain the consensus of many partitions with high modularity, rather than looking for a single partition that maximizes it. We show analytically and numerically that the proposed algorithm works all the way down to the detectability transition in networks generated by the stochastic block model. It also performs well on real-world networks, revealing large communities in some networks where previous work has claimed no communities exist. Finally we show that by applying our algorithm recursively, subdividing communities until no statistically-significant subcommunities can be found, we can detect hierarchical structure in real-world networks more efficiently than previous methods.