Fundamental limits to learning closed-form mathematical models from data

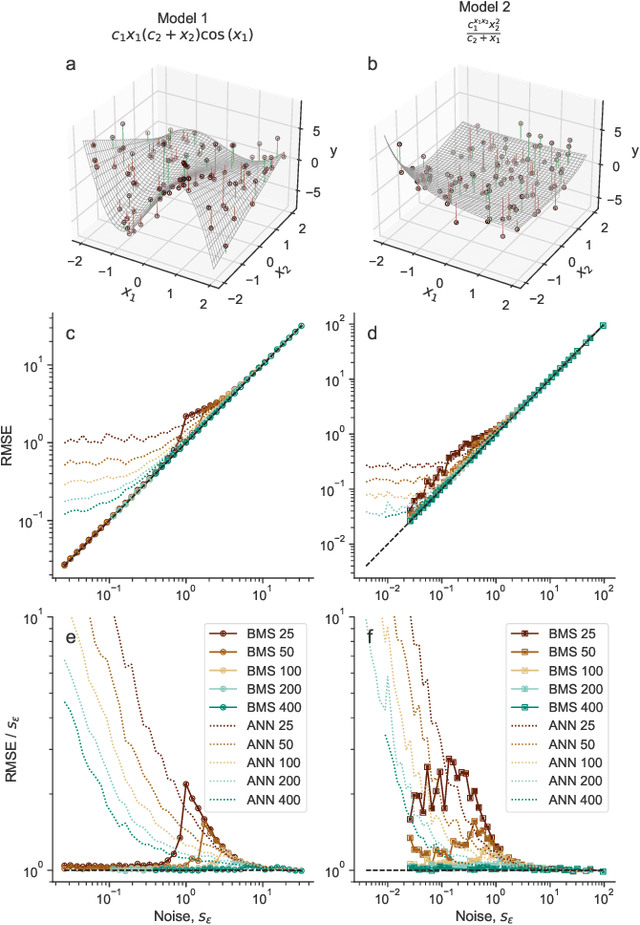
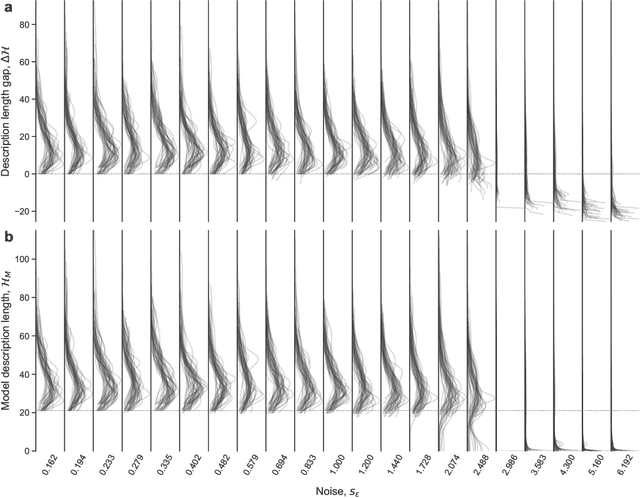
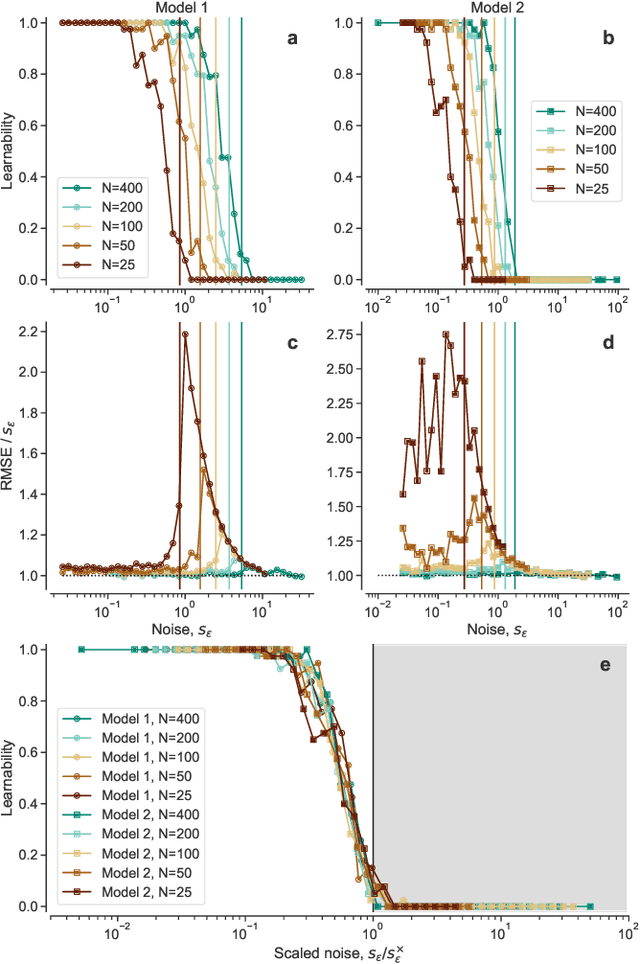
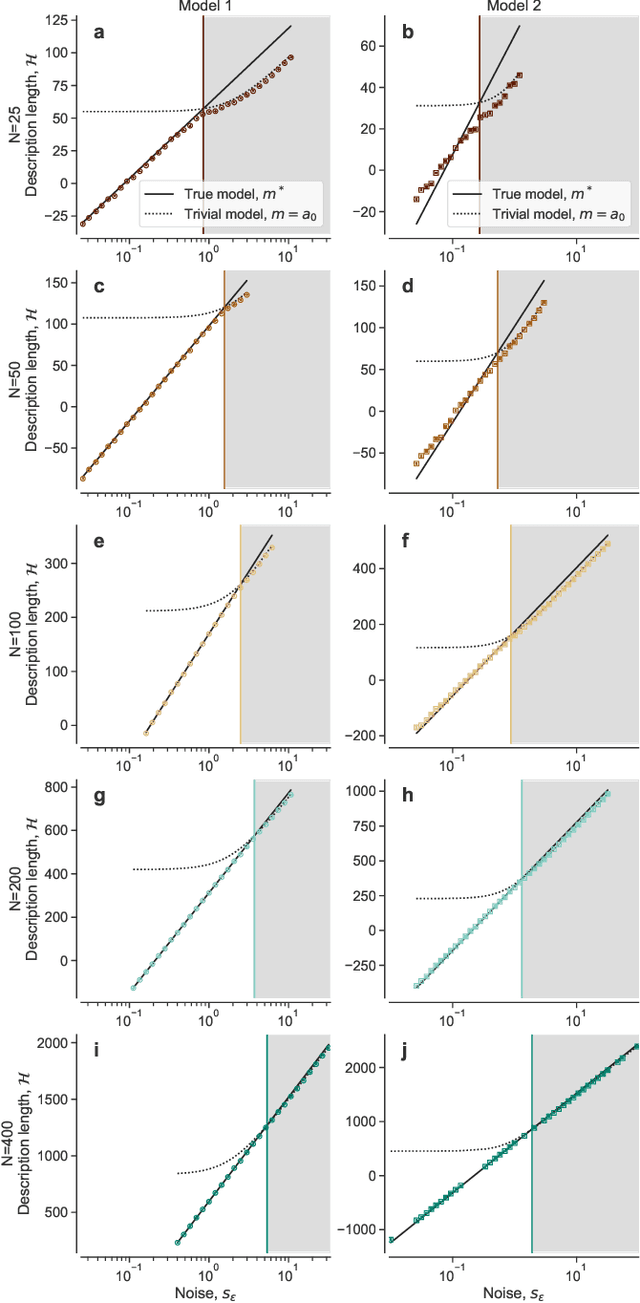
Given a finite and noisy dataset generated with a closed-form mathematical model, when is it possible to learn the true generating model from the data alone? This is the question we investigate here. We show that this model-learning problem displays a transition from a low-noise phase in which the true model can be learned, to a phase in which the observation noise is too high for the true model to be learned by any method. Both in the low-noise phase and in the high-noise phase, probabilistic model selection leads to optimal generalization to unseen data. This is in contrast to standard machine learning approaches, including artificial neural networks, which are limited, in the low-noise phase, by their ability to interpolate. In the transition region between the learnable and unlearnable phases, generalization is hard for all approaches including probabilistic model selection.

Node metadata can produce predictability transitions in network inference problems

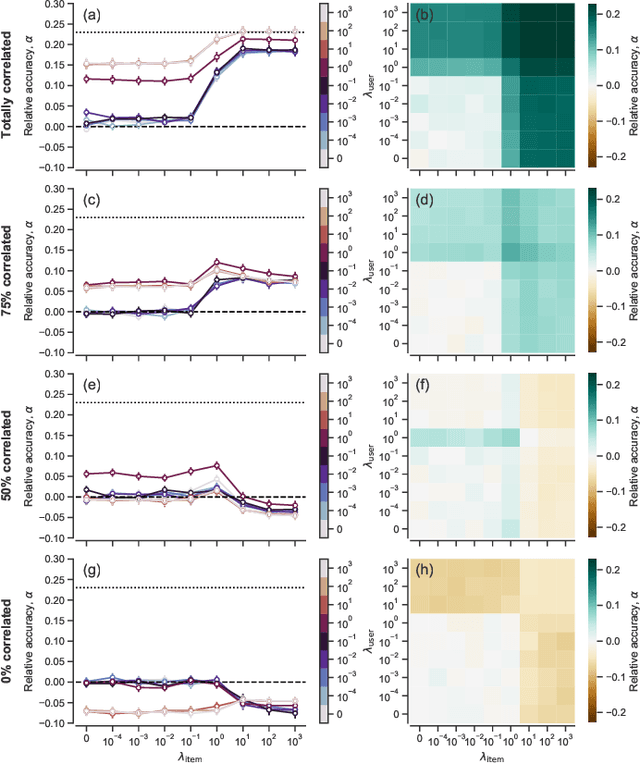
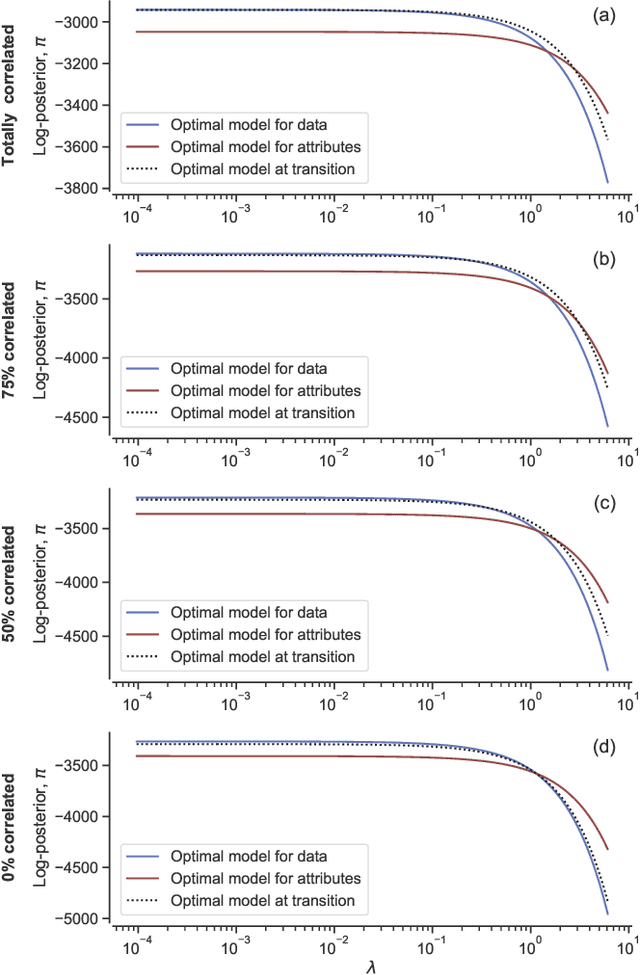
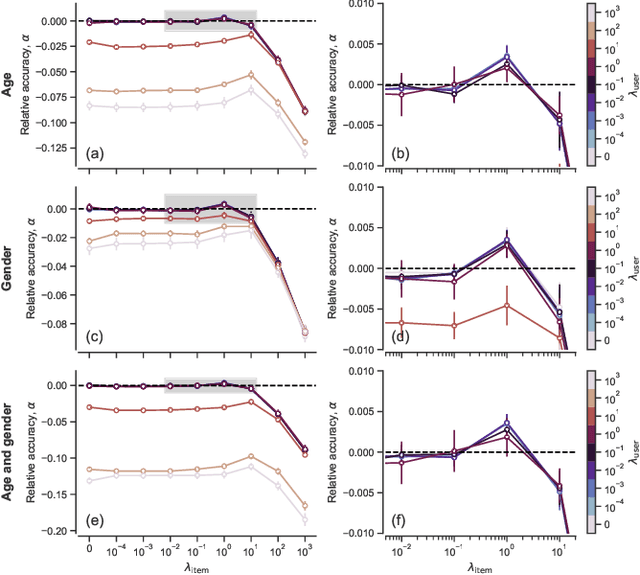
Network inference is the process of learning the properties of complex networks from data. Besides using information about known links in the network, node attributes and other forms of network metadata can help to solve network inference problems. Indeed, several approaches have been proposed to introduce metadata into probabilistic network models and to use them to make better inferences. However, we know little about the effect of such metadata in the inference process. Here, we investigate this issue. We find that, rather than affecting inference gradually, adding metadata causes abrupt transitions in the inference process and in our ability to make accurate predictions, from a situation in which metadata does not play any role to a situation in which metadata completely dominates the inference process. When network data and metadata are partly correlated, metadata optimally contributes to the inference process at the transition between data-dominated and metadata-dominated regimes.

A Bayesian machine scientist to aid in the solution of challenging scientific problems

Closed-form, interpretable mathematical models have been instrumental for advancing our understanding of the world; with the data revolution, we may now be in a position to uncover new such models for many systems from physics to the social sciences. However, to deal with increasing amounts of data, we need "machine scientists" that are able to extract these models automatically from data. Here, we introduce a Bayesian machine scientist, which establishes the plausibility of models using explicit approximations to the exact marginal posterior over models and establishes its prior expectations about models by learning from a large empirical corpus of mathematical expressions. It explores the space of models using Markov chain Monte Carlo. We show that this approach uncovers accurate models for synthetic and real data and provides out-of-sample predictions that are more accurate than those of existing approaches and of other nonparametric methods.

Network-based models for social recommender systems

With the overwhelming online products available in recent years, there is an increasing need to filter and deliver relevant personalized advice for users. Recommender systems solve this problem by modeling and predicting individual preferences for a great variety of items such as movies, books or research articles. In this chapter, we explore rigorous network-based models that outperform leading approaches for recommendation. The network models we consider are based on the explicit assumption that there are groups of individuals and of items, and that the preferences of an individual for an item are determined only by their group memberships. The accurate prediction of individual user preferences over items can be accomplished by different methodologies, such as Monte Carlo sampling or Expectation-Maximization methods, the latter resulting in a scalable algorithm which is suitable for large datasets.

Tensorial and bipartite block models for link prediction in layered networks and temporal networks

Many real-world complex systems are well represented as multilayer networks; predicting interactions in those systems is one of the most pressing problems in predictive network science. To address this challenge, we introduce two stochastic block models for multilayer and temporal networks; one of them uses nodes as its fundamental unit, whereas the other focuses on links. We also develop scalable algorithms for inferring the parameters of these models. Because our models describe all layers simultaneously, our approach takes full advantage of the information contained in the whole network when making predictions about any particular layer. We illustrate the potential of our approach by analyzing two empirical datasets---a temporal network of email communications, and a network of drug interactions for treating different cancer types. We find that modeling all layers simultaneously does result, in general, in more accurate link prediction. However, the most predictive model depends on the dataset under consideration; whereas the node-based model is more appropriate for predicting drug interactions, the link-based model is more appropriate for predicting email communication.

Accurate and scalable social recommendation using mixed-membership stochastic block models

With ever-increasing amounts of online information available, modeling and predicting individual preferences-for books or articles, for example-is becoming more and more important. Good predictions enable us to improve advice to users, and obtain a better understanding of the socio-psychological processes that determine those preferences. We have developed a collaborative filtering model, with an associated scalable algorithm, that makes accurate predictions of individuals' preferences. Our approach is based on the explicit assumption that there are groups of individuals and of items, and that the preferences of an individual for an item are determined only by their group memberships. Importantly, we allow each individual and each item to belong simultaneously to mixtures of different groups and, unlike many popular approaches, such as matrix factorization, we do not assume implicitly or explicitly that individuals in each group prefer items in a single group of items. The resulting overlapping groups and the predicted preferences can be inferred with a expectation-maximization algorithm whose running time scales linearly (per iteration). Our approach enables us to predict individual preferences in large datasets, and is considerably more accurate than the current algorithms for such large datasets.

Justice blocks and predictability of US Supreme Court votes

Successful attempts to predict judges' votes shed light into how legal decisions are made and, ultimately, into the behavior and evolution of the judiciary. Here, we investigate to what extent it is possible to make predictions of a justice's vote based on the other justices' votes in the same case. For our predictions, we use models and methods that have been developed to uncover hidden associations between actors in complex social networks. We show that these methods are more accurate at predicting justice's votes than forecasts made by legal experts and by algorithms that take into consideration the content of the cases. We argue that, within our framework, high predictability is a quantitative proxy for stable justice (and case) blocks, which probably reflect stable a priori attitudes toward the law. We find that U. S. Supreme Court justice votes are more predictable than one would expect from an ideal court composed of perfectly independent justices. Deviations from ideal behavior are most apparent in divided 5-4 decisions, where justice blocks seem to be most stable. Moreover, we find evidence that justice predictability decreased during the 50-year period spanning from the Warren Court to the Rehnquist Court, and that aggregate court predictability has been significantly lower during Democratic presidencies. More broadly, our results show that it is possible to use methods developed for the analysis of complex social networks to quantitatively investigate historical questions related to political decision-making.

Predicting human preferences using the block structure of complex social networks

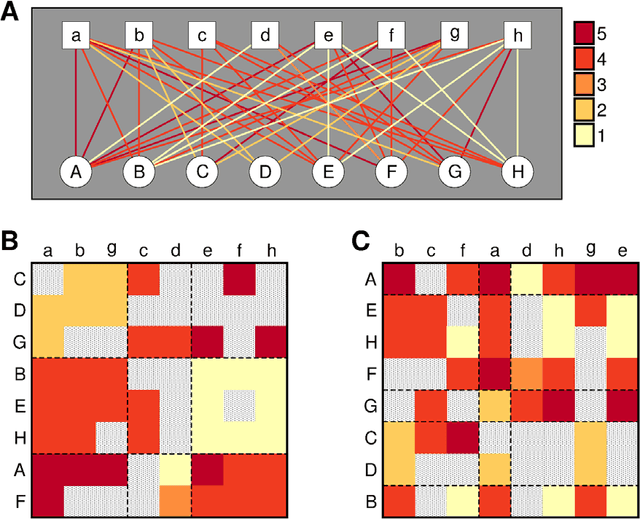
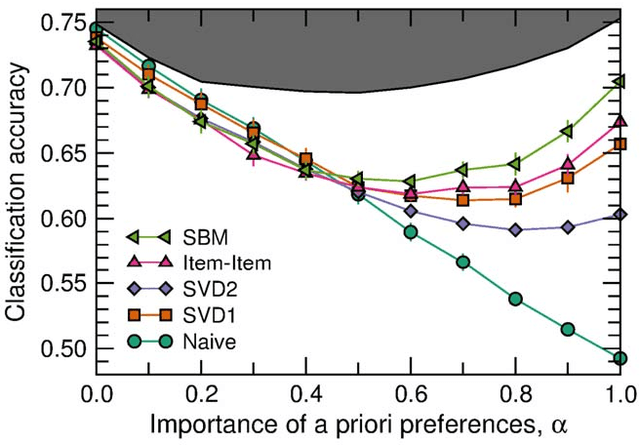
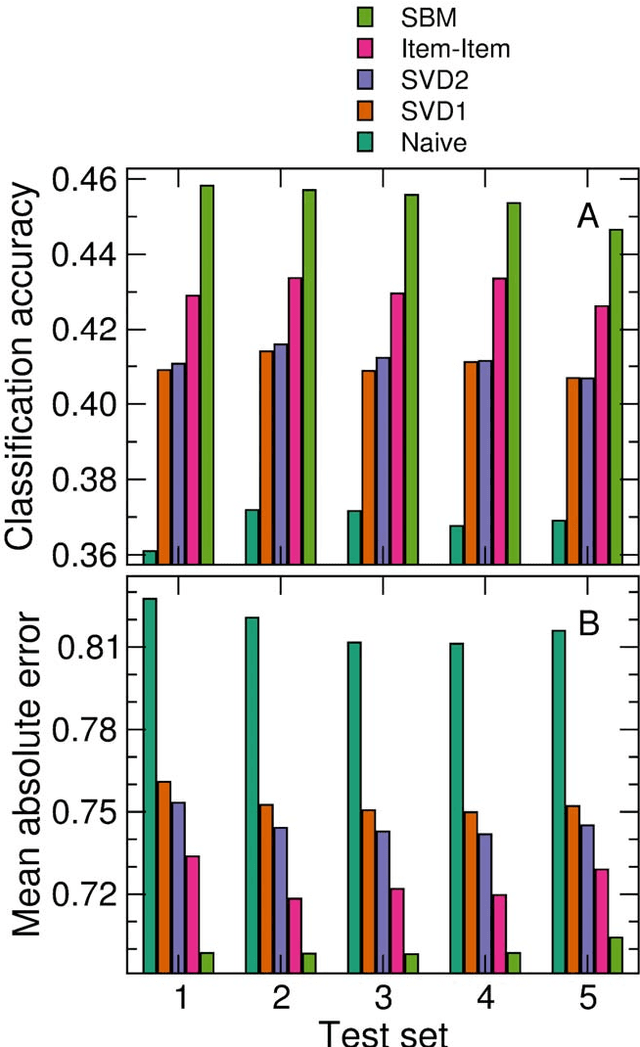
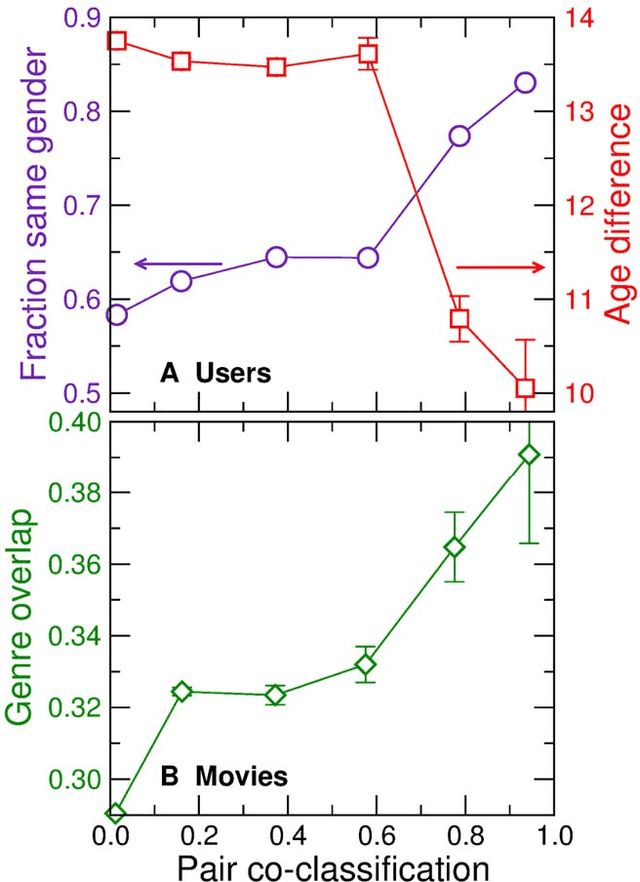
With ever-increasing available data, predicting individuals' preferences and helping them locate the most relevant information has become a pressing need. Understanding and predicting preferences is also important from a fundamental point of view, as part of what has been called a "new" computational social science. Here, we propose a novel approach based on stochastic block models, which have been developed by sociologists as plausible models of complex networks of social interactions. Our model is in the spirit of predicting individuals' preferences based on the preferences of others but, rather than fitting a particular model, we rely on a Bayesian approach that samples over the ensemble of all possible models. We show that our approach is considerably more accurate than leading recommender algorithms, with major relative improvements between 38% and 99% over industry-level algorithms. Besides, our approach sheds light on decision-making processes by identifying groups of individuals that have consistently similar preferences, and enabling the analysis of the characteristics of those groups.