Fundamental limits to learning closed-form mathematical models from data

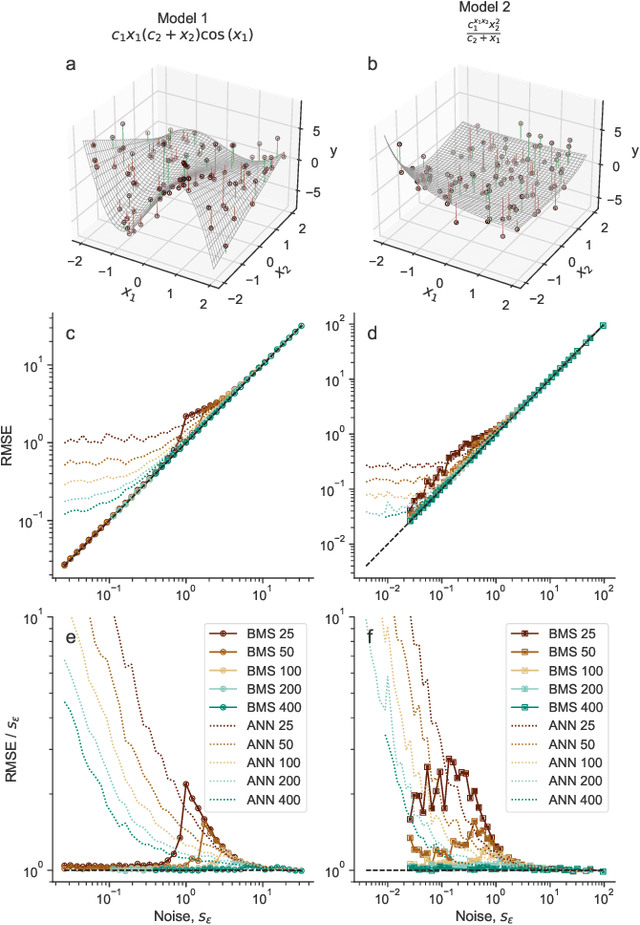
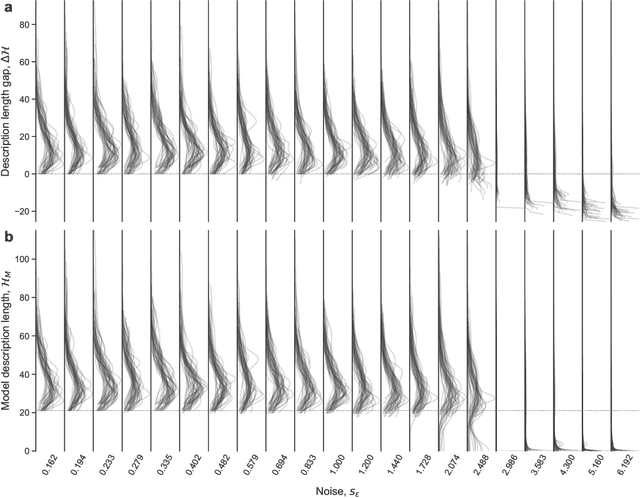
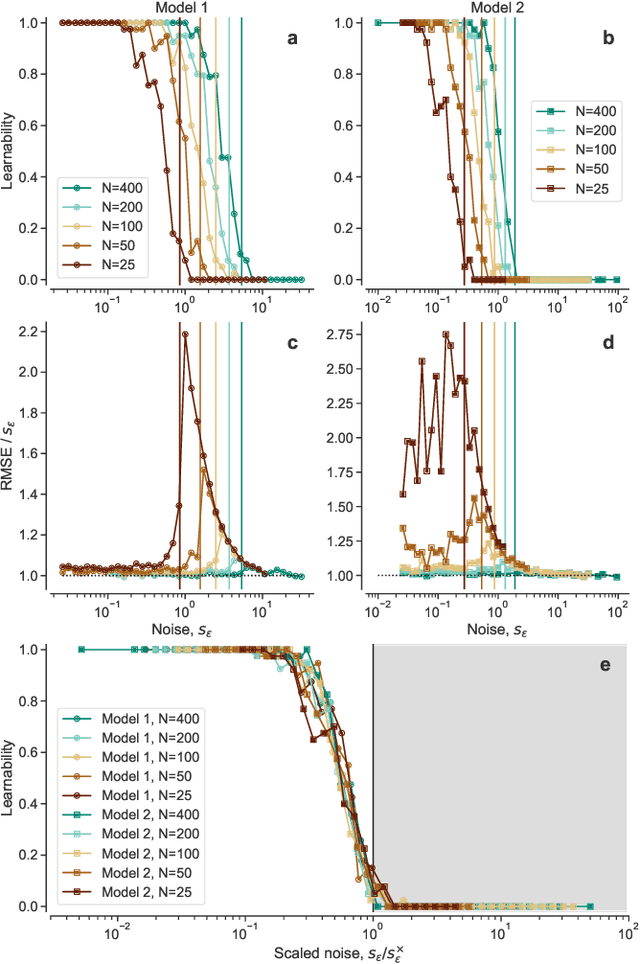
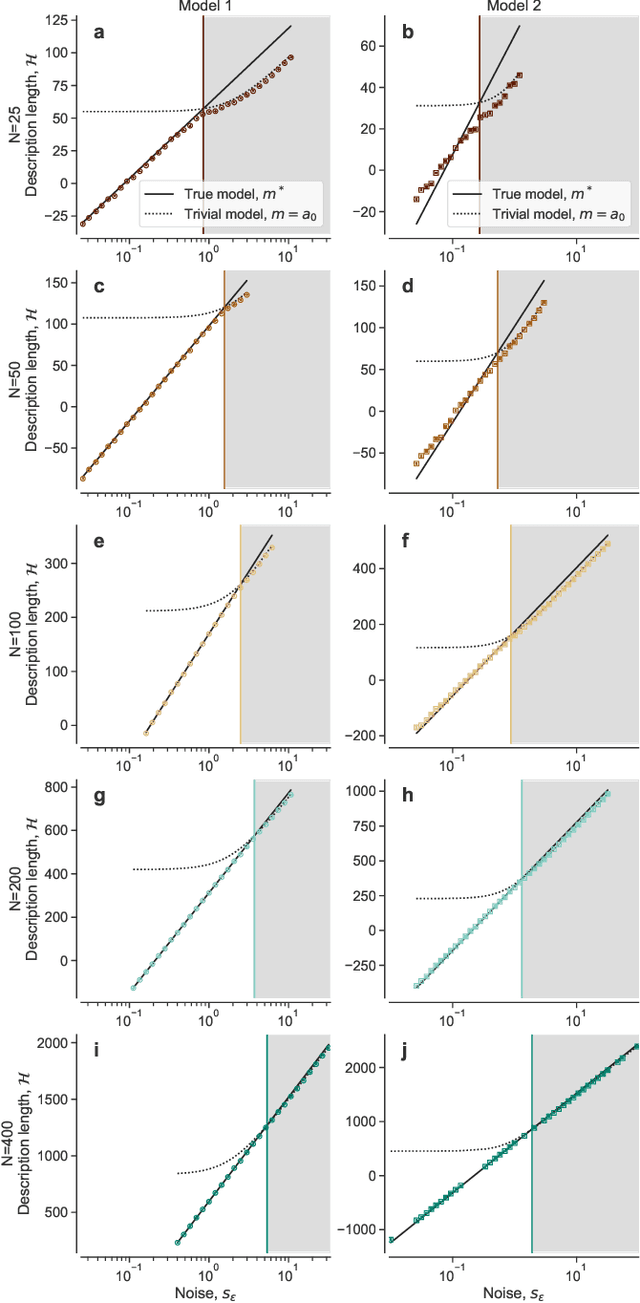
Given a finite and noisy dataset generated with a closed-form mathematical model, when is it possible to learn the true generating model from the data alone? This is the question we investigate here. We show that this model-learning problem displays a transition from a low-noise phase in which the true model can be learned, to a phase in which the observation noise is too high for the true model to be learned by any method. Both in the low-noise phase and in the high-noise phase, probabilistic model selection leads to optimal generalization to unseen data. This is in contrast to standard machine learning approaches, including artificial neural networks, which are limited, in the low-noise phase, by their ability to interpolate. In the transition region between the learnable and unlearnable phases, generalization is hard for all approaches including probabilistic model selection.

Node metadata can produce predictability transitions in network inference problems

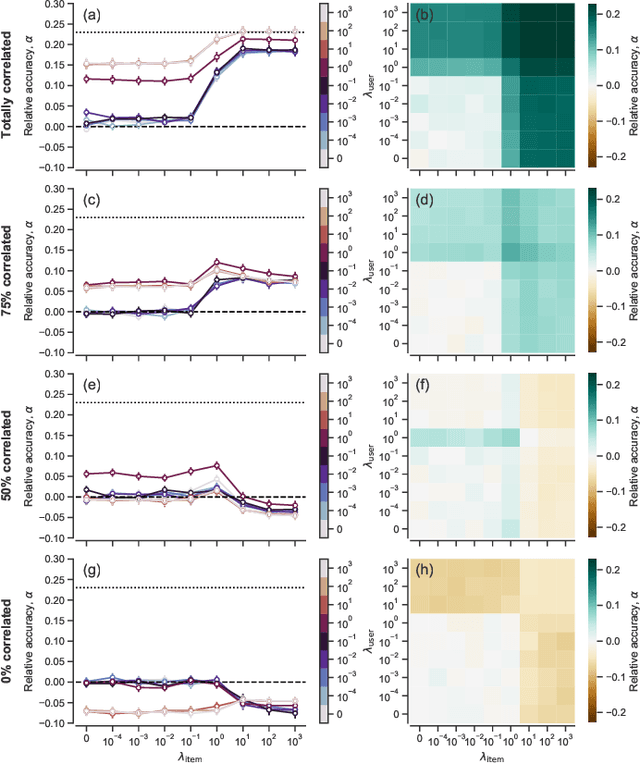
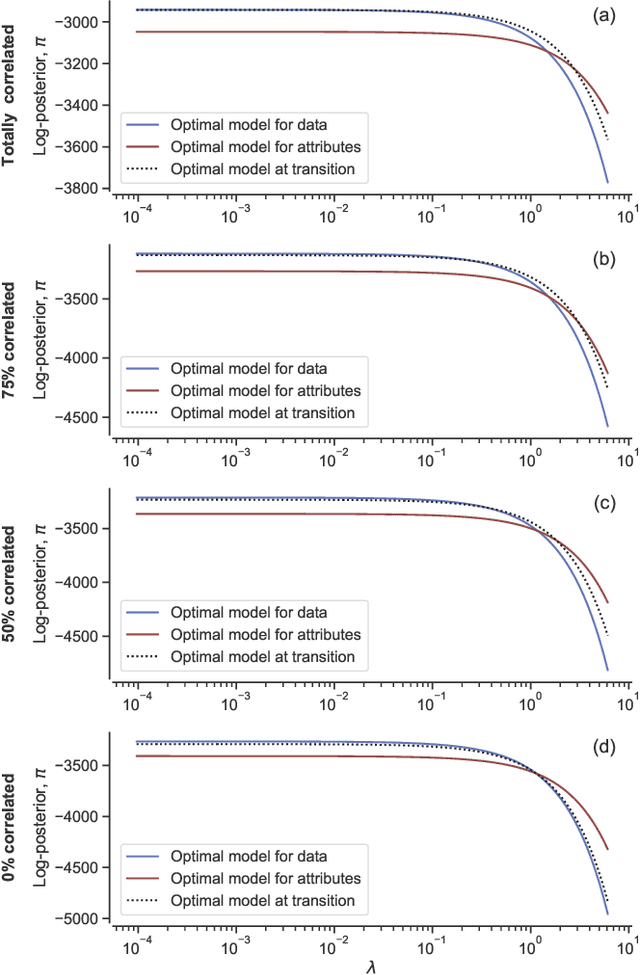
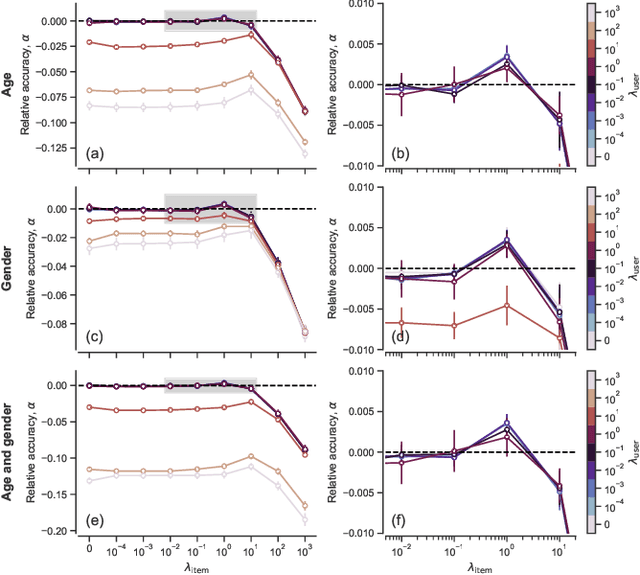
Network inference is the process of learning the properties of complex networks from data. Besides using information about known links in the network, node attributes and other forms of network metadata can help to solve network inference problems. Indeed, several approaches have been proposed to introduce metadata into probabilistic network models and to use them to make better inferences. However, we know little about the effect of such metadata in the inference process. Here, we investigate this issue. We find that, rather than affecting inference gradually, adding metadata causes abrupt transitions in the inference process and in our ability to make accurate predictions, from a situation in which metadata does not play any role to a situation in which metadata completely dominates the inference process. When network data and metadata are partly correlated, metadata optimally contributes to the inference process at the transition between data-dominated and metadata-dominated regimes.