Backward and Forward Inference in Interacting Independent-Cascade Processes: A Scalable and Convergent Message-Passing Approach

We study the problems of estimating the past and future evolutions of two diffusion processes that spread concurrently on a network. Specifically, given a known network $G=(V, \overrightarrow{E})$ and a (possibly noisy) snapshot $\mathcal{O}_n$ of its state taken at (a possibly unknown) time $W$, we wish to determine the posterior distributions of the initial state of the network and the infection times of its nodes. These distributions are useful in finding source nodes of epidemics and rumors -- $\textit{backward inference}$ -- , and estimating the spread of a fixed set of source nodes -- $\textit{forward inference}$. To model the interaction between the two processes, we study an extension of the independent-cascade (IC) model where, when a node gets infected with either process, its susceptibility to the other one changes. First, we derive the exact joint probability of the initial state of the network and the observation-snapshot $\mathcal{O}_n$. Then, using the machinery of factor-graphs, factor-graph transformations, and the generalized distributive-law, we derive a Belief-Propagation (BP) based algorithm that is scalable to large networks and can converge on graphs of arbitrary topology (at a likely expense in approximation accuracy).

Performance Bounds for Policy-Based Average Reward Reinforcement Learning Algorithms

Many policy-based reinforcement learning (RL) algorithms can be viewed as instantiations of approximate policy iteration (PI), i.e., where policy improvement and policy evaluation are both performed approximately. In applications where the average reward objective is the meaningful performance metric, often discounted reward formulations are used with the discount factor being close to 1, which is equivalent to making the expected horizon very large. However, the corresponding theoretical bounds for error performance scale with the square of the horizon. Thus, even after dividing the total reward by the length of the horizon, the corresponding performance bounds for average reward problems go to infinity. Therefore, an open problem has been to obtain meaningful performance bounds for approximate PI and RL algorithms for the average-reward setting. In this paper, we solve this open problem by obtaining the first non-trivial error bounds for average-reward MDPs which go to zero in the limit where when policy evaluation and policy improvement errors go to zero.

Modified Policy Iteration for Exponential Cost Risk Sensitive MDPs

Modified policy iteration (MPI) also known as optimistic policy iteration is at the core of many reinforcement learning algorithms. It works by combining elements of policy iteration and value iteration. The convergence of MPI has been well studied in the case of discounted and average-cost MDPs. In this work, we consider the exponential cost risk-sensitive MDP formulation, which is known to provide some robustness to model parameters. Although policy iteration and value iteration have been well studied in the context of risk sensitive MDPs, modified policy iteration is relatively unexplored. We provide the first proof that MPI also converges for the risk-sensitive problem in the case of finite state and action spaces. Since the exponential cost formulation deals with the multiplicative Bellman equation, our main contribution is a convergence proof which is quite different than existing results for discounted and risk-neutral average-cost problems. The proof of approximate modified policy iteration for risk sensitive MDPs is also provided in the appendix.

Learning a Discrete Set of Optimal Allocation Rules in Queueing Systems with Unknown Service Rates

We study learning-based admission control for a classical Erlang-B blocking system with unknown service rate, i.e., an $M/M/k/k$ queueing system. At every job arrival, a dispatcher decides to assign the job to an available server or to block it. Every served job yields a fixed reward for the dispatcher, but it also results in a cost per unit time of service. Our goal is to design a dispatching policy that maximizes the long-term average reward for the dispatcher based on observing the arrival times and the state of the system at each arrival; critically, the dispatcher observes neither the service times nor departure times. We develop our learning-based dispatch scheme as a parametric learning problem a'la self-tuning adaptive control. In our problem, certainty equivalent control switches between an always admit policy (always explore) and a never admit policy (immediately terminate learning), which is distinct from the adaptive control literature. Our learning scheme then uses maximum likelihood estimation followed by certainty equivalent control but with judicious use of the always admit policy so that learning doesn't stall. We prove that for all service rates, the proposed policy asymptotically learns to take the optimal action. Further, we also present finite-time regret guarantees for our scheme. The extreme contrast in the certainty equivalent optimal control policies leads to difficulties in learning that show up in our regret bounds for different parameter regimes. We explore this aspect in our simulations and also follow-up sampling related questions for our continuous-time system.

The Planted Matching Problem: Phase Transitions and Exact Results

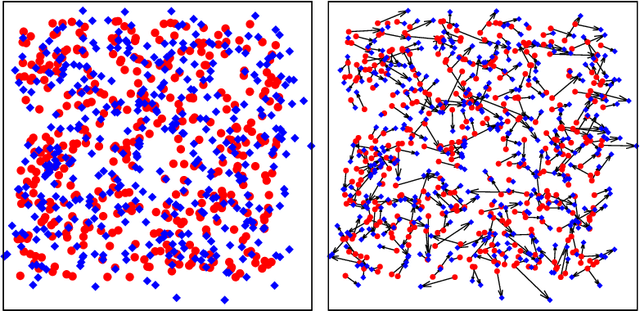
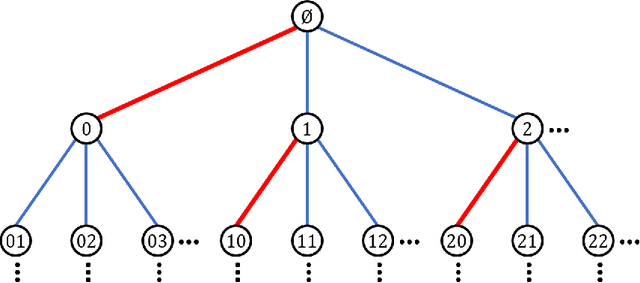
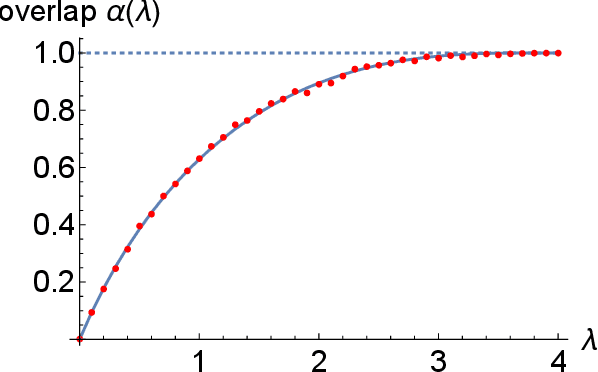
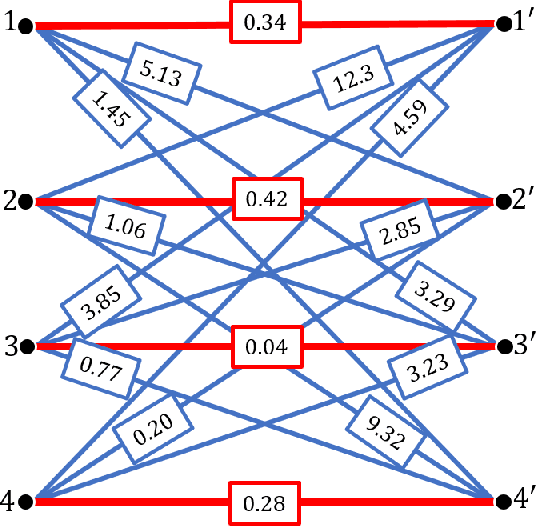
We study the problem of recovering a planted matching in randomly weighted complete bipartite graphs $K_{n,n}$. For some unknown perfect matching $M^*$, the weight of an edge is drawn from one distribution $P$ if $e \in M^*$ and another distribution $Q$ if $e \in M^*$. Our goal is to infer $M^*$, exactly or approximately, from the edge weights. In this paper we take $P=\exp(\lambda)$ and $Q=\exp(1/n)$, in which case the maximum-likelihood estimator of $M^*$ is the minimum-weight matching $M_{\min}$. We obtain precise results on the overlap between $M^*$ and $M_{\min}$, i.e., the fraction of edges they have in common. For $\lambda \ge 4$ we have almost-perfect recovery, with overlap $1-o(1)$ with high probability. For $\lambda < 4$ the expected overlap is an explicit function $\alpha(\lambda) < 1$: we compute it by generalizing Aldous' celebrated proof of M\'ezard and Parisi's $\zeta(2)$ conjecture for the un-planted model, using local weak convergence to relate $K_{n,n}$ to a type of weighted infinite tree, and then deriving a system of differential equations from a message-passing algorithm on this tree.