Backward and Forward Inference in Interacting Independent-Cascade Processes: A Scalable and Convergent Message-Passing Approach

We study the problems of estimating the past and future evolutions of two diffusion processes that spread concurrently on a network. Specifically, given a known network $G=(V, \overrightarrow{E})$ and a (possibly noisy) snapshot $\mathcal{O}_n$ of its state taken at (a possibly unknown) time $W$, we wish to determine the posterior distributions of the initial state of the network and the infection times of its nodes. These distributions are useful in finding source nodes of epidemics and rumors -- $\textit{backward inference}$ -- , and estimating the spread of a fixed set of source nodes -- $\textit{forward inference}$. To model the interaction between the two processes, we study an extension of the independent-cascade (IC) model where, when a node gets infected with either process, its susceptibility to the other one changes. First, we derive the exact joint probability of the initial state of the network and the observation-snapshot $\mathcal{O}_n$. Then, using the machinery of factor-graphs, factor-graph transformations, and the generalized distributive-law, we derive a Belief-Propagation (BP) based algorithm that is scalable to large networks and can converge on graphs of arbitrary topology (at a likely expense in approximation accuracy).

Bayesian Learning of Optimal Policies in Markov Decision Processes with Countably Infinite State-Space

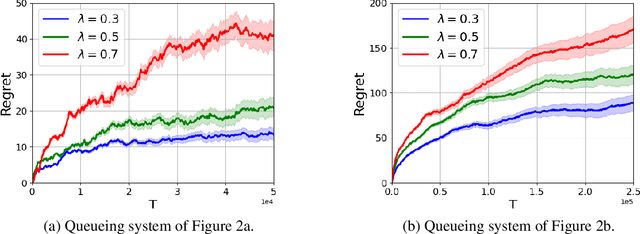
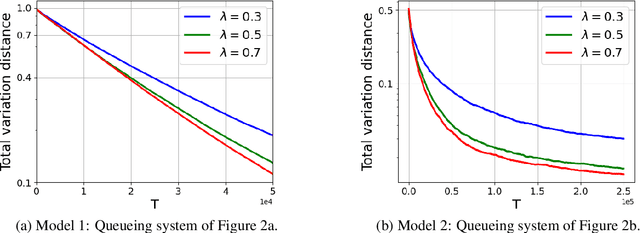
Models of many real-life applications, such as queuing models of communication networks or computing systems, have a countably infinite state-space. Algorithmic and learning procedures that have been developed to produce optimal policies mainly focus on finite state settings, and do not directly apply to these models. To overcome this lacuna, in this work we study the problem of optimal control of a family of discrete-time countable state-space Markov Decision Processes (MDPs) governed by an unknown parameter $\theta\in\Theta$, and defined on a countably-infinite state space $\mathcal X=\mathbb{Z}_+^d$, with finite action space $\mathcal A$, and an unbounded cost function. We take a Bayesian perspective with the random unknown parameter $\boldsymbol{\theta}^*$ generated via a given fixed prior distribution on $\Theta$. To optimally control the unknown MDP, we propose an algorithm based on Thompson sampling with dynamically-sized episodes: at the beginning of each episode, the posterior distribution formed via Bayes' rule is used to produce a parameter estimate, which then decides the policy applied during the episode. To ensure the stability of the Markov chain obtained by following the policy chosen for each parameter, we impose ergodicity assumptions. From this condition and using the solution of the average cost Bellman equation, we establish an $\tilde O(\sqrt{|\mathcal A|T})$ upper bound on the Bayesian regret of our algorithm, where $T$ is the time-horizon. Finally, to elucidate the applicability of our algorithm, we consider two different queuing models with unknown dynamics, and show that our algorithm can be applied to develop approximately optimal control algorithms.

OpenGridGym: An Open-Source AI-Friendly Toolkit for Distribution Market Simulation

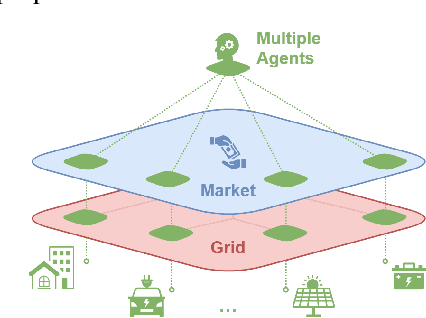
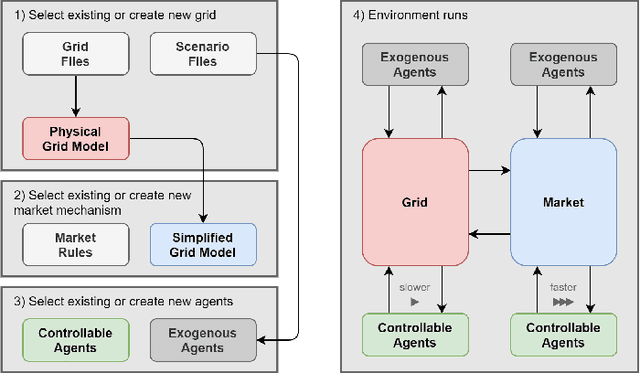
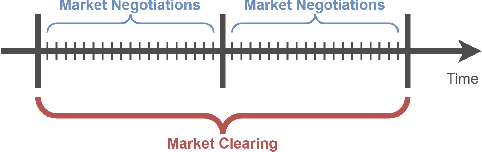
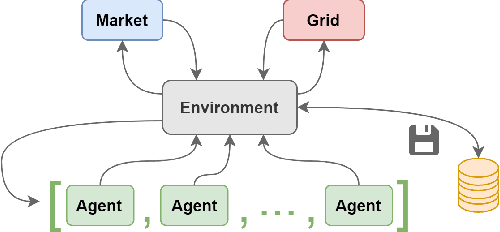
This paper presents OpenGridGym, an open-source Python-based package that allows for seamless integration of distribution market simulation with state-of-the-art artificial intelligence (AI) decision-making algorithms. We present the architecture and design choice for the proposed framework, elaborate on how users interact with OpenGridGym, and highlight its value by providing multiple cases to demonstrate its use. Four modules are used in any simulation: (1) the physical grid, (2) market mechanisms, (3) a set of trainable agents which interact with the former two modules, and (4) environment module that connects and coordinates the above three. We provide templates for each of those four, but they are easily interchangeable with custom alternatives. Several case studies are presented to illustrate the capability and potential of this toolkit in helping researchers address key design and operational questions in distribution electricity markets.

Learning a Discrete Set of Optimal Allocation Rules in Queueing Systems with Unknown Service Rates

We study learning-based admission control for a classical Erlang-B blocking system with unknown service rate, i.e., an $M/M/k/k$ queueing system. At every job arrival, a dispatcher decides to assign the job to an available server or to block it. Every served job yields a fixed reward for the dispatcher, but it also results in a cost per unit time of service. Our goal is to design a dispatching policy that maximizes the long-term average reward for the dispatcher based on observing the arrival times and the state of the system at each arrival; critically, the dispatcher observes neither the service times nor departure times. We develop our learning-based dispatch scheme as a parametric learning problem a'la self-tuning adaptive control. In our problem, certainty equivalent control switches between an always admit policy (always explore) and a never admit policy (immediately terminate learning), which is distinct from the adaptive control literature. Our learning scheme then uses maximum likelihood estimation followed by certainty equivalent control but with judicious use of the always admit policy so that learning doesn't stall. We prove that for all service rates, the proposed policy asymptotically learns to take the optimal action. Further, we also present finite-time regret guarantees for our scheme. The extreme contrast in the certainty equivalent optimal control policies leads to difficulties in learning that show up in our regret bounds for different parameter regimes. We explore this aspect in our simulations and also follow-up sampling related questions for our continuous-time system.

Decentralized Cooperative Reinforcement Learning with Hierarchical Information Structure

Multi-agent reinforcement learning (MARL) problems are challenging due to information asymmetry. To overcome this challenge, existing methods often require high level of coordination or communication between the agents. We consider two-agent multi-armed bandits (MABs) and Markov decision processes (MDPs) with a hierarchical information structure arising in applications, which we exploit to propose simpler and more efficient algorithms that require no coordination or communication. In the structure, in each step the ``leader" chooses her action first, and then the ``follower" decides his action after observing the leader's action. The two agents observe the same reward (and the same state transition in the MDP setting) that depends on their joint action. For the bandit setting, we propose a hierarchical bandit algorithm that achieves a near-optimal gap-independent regret of $\widetilde{\mathcal{O}}(\sqrt{ABT})$ and a near-optimal gap-dependent regret of $\mathcal{O}(\log(T))$, where $A$ and $B$ are the numbers of actions of the leader and the follower, respectively, and $T$ is the number of steps. We further extend to the case of multiple followers and the case with a deep hierarchy, where we both obtain near-optimal regret bounds. For the MDP setting, we obtain $\widetilde{\mathcal{O}}(\sqrt{H^7S^2ABT})$ regret, where $H$ is the number of steps per episode, $S$ is the number of states, $T$ is the number of episodes. This matches the existing lower bound in terms of $A, B$, and $T$.

Common Information based Approximate State Representations in Multi-Agent Reinforcement Learning

Due to information asymmetry, finding optimal policies for Decentralized Partially Observable Markov Decision Processes (Dec-POMDPs) is hard with the complexity growing doubly exponentially in the horizon length. The challenge increases greatly in the multi-agent reinforcement learning (MARL) setting where the transition probabilities, observation kernel, and reward function are unknown. Here, we develop a general compression framework with approximate common and private state representations, based on which decentralized policies can be constructed. We derive the optimality gap of executing dynamic programming (DP) with the approximate states in terms of the approximation error parameters and the remaining time steps. When the compression is exact (no error), the resulting DP is equivalent to the one in existing work. Our general framework generalizes a number of methods proposed in the literature. The results shed light on designing practically useful deep-MARL network structures under the "centralized learning distributed execution" scheme.

Empirical Policy Evaluation with Supergraphs

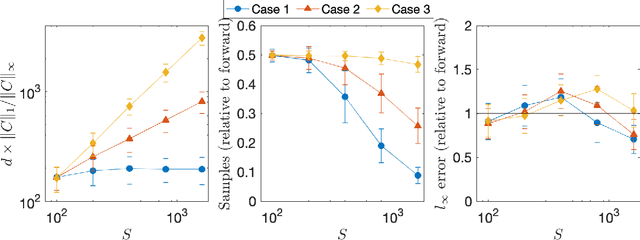
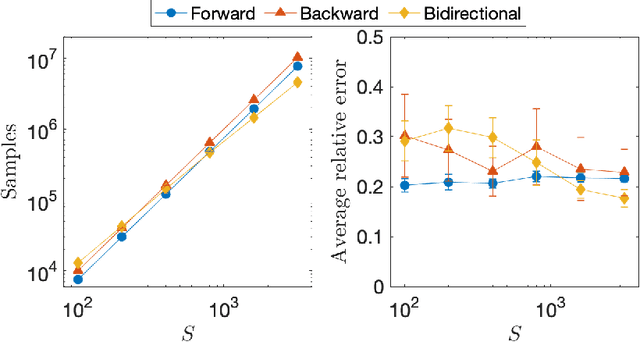
We devise and analyze algorithms for the empirical policy evaluation problem in reinforcement learning. Our algorithms explore backward from high-cost states to find high-value ones, in contrast to forward approaches that work forward from all states. While several papers have demonstrated the utility of backward exploration empirically, we conduct rigorous analyses which show that our algorithms can reduce average-case sample complexity from $O(S \log S)$ to as low as $O(\log S)$.