Collaborative Multi-Agent Heterogeneous Multi-Armed Bandits

The study of collaborative multi-agent bandits has attracted significant attention recently. In light of this, we initiate the study of a new collaborative setting, consisting of $N$ agents such that each agent is learning one of $M$ stochastic multi-armed bandits to minimize their group cumulative regret. We develop decentralized algorithms which facilitate collaboration between the agents under two scenarios. We characterize the performance of these algorithms by deriving the per agent cumulative regret and group regret upper bounds. We also prove lower bounds for the group regret in this setting, which demonstrates the near-optimal behavior of the proposed algorithms.

Minimax Regret for Cascading Bandits

Cascading bandits model the task of learning to rank $K$ out of $L$ items over $n$ rounds of partial feedback. For this model, the minimax (i.e., gap-free) regret is poorly understood; in particular, the best known lower and upper bounds are $\Omega(\sqrt{nL/K})$ and $\tilde{O}(\sqrt{nLK})$, respectively. We improve the lower bound to $\Omega(\sqrt{nL})$ and show CascadeKL-UCB (which ranks items by their KL-UCB indices) attains it up to log terms. Surprisingly, we also show CascadeUCB1 (which ranks via UCB1) can suffer suboptimal $\Omega(\sqrt{nLK})$ regret. This sharply contrasts with standard $L$-armed bandits, where the corresponding algorithms both achieve the minimax regret $\sqrt{nL}$ (up to log terms), and the main advantage of KL-UCB is only to improve constants in the gap-dependent bounds. In essence, this contrast occurs because Pinsker's inequality is tight for hard problems in the $L$-armed case but loose (by a factor of $K$) in the cascading case.

Robust Multi-Agent Bandits Over Undirected Graphs

We consider a multi-agent multi-armed bandit setting in which $n$ honest agents collaborate over a network to minimize regret but $m$ malicious agents can disrupt learning arbitrarily. Assuming the network is the complete graph, existing algorithms incur $O( (m + K/n) \log (T) / \Delta )$ regret in this setting, where $K$ is the number of arms and $\Delta$ is the arm gap. For $m \ll K$, this improves over the single-agent baseline regret of $O(K\log(T)/\Delta)$. In this work, we show the situation is murkier beyond the case of a complete graph. In particular, we prove that if the state-of-the-art algorithm is used on the undirected line graph, honest agents can suffer (nearly) linear regret until time is doubly exponential in $K$ and $n$. In light of this negative result, we propose a new algorithm for which the $i$-th agent has regret $O( ( d_{\text{mal}}(i) + K/n) \log(T)/\Delta)$ on any connected and undirected graph, where $d_{\text{mal}}(i)$ is the number of $i$'s neighbors who are malicious. Thus, we generalize existing regret bounds beyond the complete graph (where $d_{\text{mal}}(i) = m$), and show the effect of malicious agents is entirely local (in the sense that only the $d_{\text{mal}}(i)$ malicious agents directly connected to $i$ affect its long-term regret).

Improved Algorithms for Misspecified Linear Markov Decision Processes

For the misspecified linear Markov decision process (MLMDP) model of Jin et al. [2020], we propose an algorithm with three desirable properties. (P1) Its regret after $K$ episodes scales as $K \max \{ \varepsilon_{\text{mis}}, \varepsilon_{\text{tol}} \}$, where $\varepsilon_{\text{mis}}$ is the degree of misspecification and $\varepsilon_{\text{tol}}$ is a user-specified error tolerance. (P2) Its space and per-episode time complexities remain bounded as $K \rightarrow \infty$. (P3) It does not require $\varepsilon_{\text{mis}}$ as input. To our knowledge, this is the first algorithm satisfying all three properties. For concrete choices of $\varepsilon_{\text{tol}}$, we also improve existing regret bounds (up to log factors) while achieving either (P2) or (P3) (existing algorithms satisfy neither). At a high level, our algorithm generalizes (to MLMDPs) and refines the Sup-Lin-UCB algorithm, which Takemura et al. [2021] recently showed satisfies (P3) in the contextual bandit setting.

Regret Bounds for Stochastic Shortest Path Problems with Linear Function Approximation

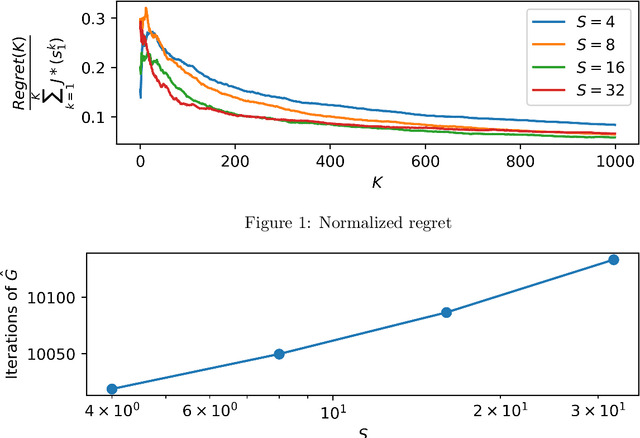
We propose two algorithms for episodic stochastic shortest path problems with linear function approximation. The first is computationally expensive but provably obtains $\tilde{O} (\sqrt{B_\star^3 d^3 K/c_{min}} )$ regret, where $B_\star$ is a (known) upper bound on the optimal cost-to-go function, $d$ is the feature dimension, $K$ is the number of episodes, and $c_{min}$ is the minimal cost of non-goal state-action pairs (assumed to be positive). The second is computationally efficient in practice, and we conjecture that it obtains the same regret bound. Both algorithms are based on an optimistic least-squares version of value iteration analogous to the finite-horizon backward induction approach from Jin et al. 2020. To the best of our knowledge, these are the first regret bounds for stochastic shortest path that are independent of the size of the state and action spaces.

One-bit feedback is sufficient for upper confidence bound policies

We consider a variant of the traditional multi-armed bandit problem in which each arm is only able to provide one-bit feedback during each pull based on its past history of rewards. Our main result is the following: given an upper confidence bound policy which uses full-reward feedback, there exists a coding scheme for generating one-bit feedback, and a corresponding decoding scheme and arm selection policy, such that the ratio of the regret achieved by our policy and the regret of the full-reward feedback policy asymptotically approaches one.

Robust Multi-Agent Multi-Armed Bandits

There has been recent interest in collaborative multi-agent bandits, where groups of agents share recommendations to decrease per-agent regret. However, these works assume that each agent always recommends their individual best-arm estimates to other agents, which is unrealistic in envisioned applications (machine faults in distributed computing or spam in social recommendation systems). Hence, we generalize the setting to include honest and malicious agents who recommend best-arm estimates and arbitrary arms, respectively. We show that even with a single malicious agent, existing collaboration-based algorithms fail to improve regret guarantees over a single-agent baseline. We propose a scheme where honest agents learn who is malicious and dynamically reduce communication with them, i.e., "blacklist" them. We show that collaboration indeed decreases regret for this algorithm, when the number of malicious agents is small compared to the number of arms, and crucially without assumptions on the malicious agents' behavior. Thus, our algorithm is robust against any malicious recommendation strategy.

Empirical Policy Evaluation with Supergraphs

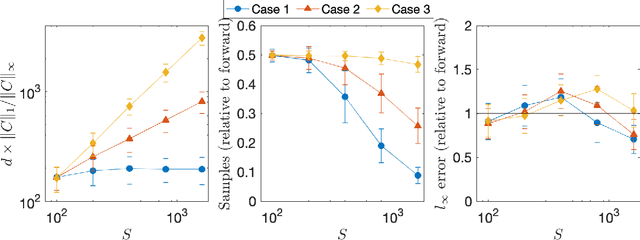
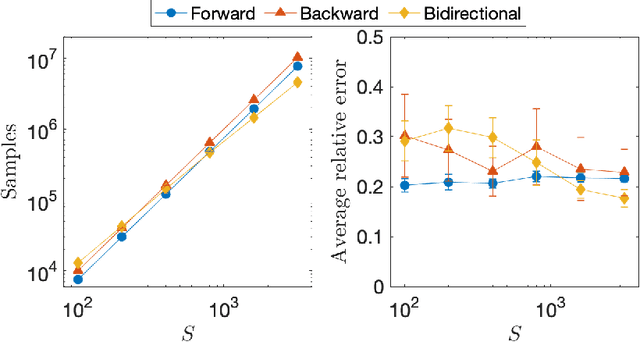
We devise and analyze algorithms for the empirical policy evaluation problem in reinforcement learning. Our algorithms explore backward from high-cost states to find high-value ones, in contrast to forward approaches that work forward from all states. While several papers have demonstrated the utility of backward exploration empirically, we conduct rigorous analyses which show that our algorithms can reduce average-case sample complexity from $O(S \log S)$ to as low as $O(\log S)$.