Super-resolution ranging using a sub-terahertz self-injection-locked frequency-modulated radar

Sub-terahertz (sub-THz) and terahertz (THz) frequency-modulated continuous-wave (FMCW) radars have opened a plethora of scientific and industrial applications, especially in the imaging field. While strong candidates for sub-THz/THz FMCW radar imagers are implemented using photonic methods, there is a desire to achieve the full integration and portability that only electronics can offer. However, integrated electronic sub-THz/THz FMCW radars have significantly lower bandwidth (< 100 GHz) than photonic-based radars, restricting the radar range resolution to the millimeter scale (> 1.5 mm). In addition, the electronic FMCW radar's broad bandwidth comes with increased transmitter phase noise, consequently degrading the radar range accuracy. Here, we present a sub-THz fully-integrated autodyne frequency-modulated (AFM) radar utilizing a self-injection locking (SIL) mechanism that fundamentally overcomes the aforementioned challenges of FMCW radars. The AFM radar supports an exceptionally wide effective bandwidth extending into the terahertz sweep range by forming an intermediate frequency comb spectrum in a quadratic receiver, unlocking the path for super-resolution ranging. Furthermore, SIL significantly reduces the transmitter's phase noise, allowing high-accuracy range measurements. We theoretically describe and experimentally demonstrate the SIL operation of the AFM radar. The proposed radar experimentally achieves sub-millimeter range resolution and a range accuracy of < 0.002%, enabling the imaging of covered printed letters with micrometer features.

Bayesian Learning of Optimal Policies in Markov Decision Processes with Countably Infinite State-Space

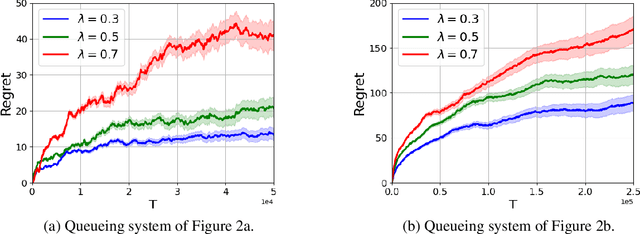
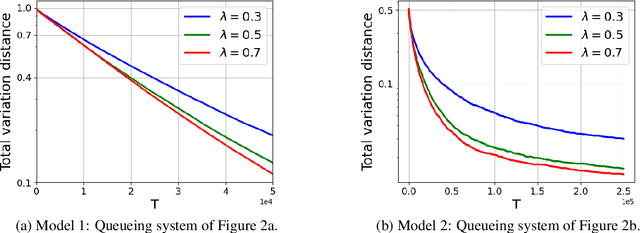
Models of many real-life applications, such as queuing models of communication networks or computing systems, have a countably infinite state-space. Algorithmic and learning procedures that have been developed to produce optimal policies mainly focus on finite state settings, and do not directly apply to these models. To overcome this lacuna, in this work we study the problem of optimal control of a family of discrete-time countable state-space Markov Decision Processes (MDPs) governed by an unknown parameter $\theta\in\Theta$, and defined on a countably-infinite state space $\mathcal X=\mathbb{Z}_+^d$, with finite action space $\mathcal A$, and an unbounded cost function. We take a Bayesian perspective with the random unknown parameter $\boldsymbol{\theta}^*$ generated via a given fixed prior distribution on $\Theta$. To optimally control the unknown MDP, we propose an algorithm based on Thompson sampling with dynamically-sized episodes: at the beginning of each episode, the posterior distribution formed via Bayes' rule is used to produce a parameter estimate, which then decides the policy applied during the episode. To ensure the stability of the Markov chain obtained by following the policy chosen for each parameter, we impose ergodicity assumptions. From this condition and using the solution of the average cost Bellman equation, we establish an $\tilde O(\sqrt{|\mathcal A|T})$ upper bound on the Bayesian regret of our algorithm, where $T$ is the time-horizon. Finally, to elucidate the applicability of our algorithm, we consider two different queuing models with unknown dynamics, and show that our algorithm can be applied to develop approximately optimal control algorithms.

Learning a Discrete Set of Optimal Allocation Rules in Queueing Systems with Unknown Service Rates

We study learning-based admission control for a classical Erlang-B blocking system with unknown service rate, i.e., an $M/M/k/k$ queueing system. At every job arrival, a dispatcher decides to assign the job to an available server or to block it. Every served job yields a fixed reward for the dispatcher, but it also results in a cost per unit time of service. Our goal is to design a dispatching policy that maximizes the long-term average reward for the dispatcher based on observing the arrival times and the state of the system at each arrival; critically, the dispatcher observes neither the service times nor departure times. We develop our learning-based dispatch scheme as a parametric learning problem a'la self-tuning adaptive control. In our problem, certainty equivalent control switches between an always admit policy (always explore) and a never admit policy (immediately terminate learning), which is distinct from the adaptive control literature. Our learning scheme then uses maximum likelihood estimation followed by certainty equivalent control but with judicious use of the always admit policy so that learning doesn't stall. We prove that for all service rates, the proposed policy asymptotically learns to take the optimal action. Further, we also present finite-time regret guarantees for our scheme. The extreme contrast in the certainty equivalent optimal control policies leads to difficulties in learning that show up in our regret bounds for different parameter regimes. We explore this aspect in our simulations and also follow-up sampling related questions for our continuous-time system.