The Franz-Parisi Criterion and Computational Trade-offs in High Dimensional Statistics

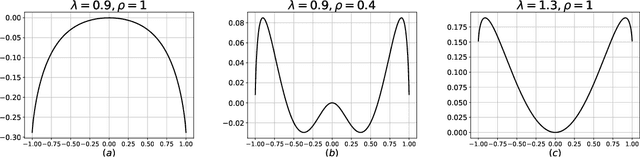
Many high-dimensional statistical inference problems are believed to possess inherent computational hardness. Various frameworks have been proposed to give rigorous evidence for such hardness, including lower bounds against restricted models of computation (such as low-degree functions), as well as methods rooted in statistical physics that are based on free energy landscapes. This paper aims to make a rigorous connection between the seemingly different low-degree and free-energy based approaches. We define a free-energy based criterion for hardness and formally connect it to the well-established notion of low-degree hardness for a broad class of statistical problems, namely all Gaussian additive models and certain models with a sparse planted signal. By leveraging these rigorous connections we are able to: establish that for Gaussian additive models the "algebraic" notion of low-degree hardness implies failure of "geometric" local MCMC algorithms, and provide new low-degree lower bounds for sparse linear regression which seem difficult to prove directly. These results provide both conceptual insights into the connections between different notions of hardness, as well as concrete technical tools such as new methods for proving low-degree lower bounds.

Imputation for High-Dimensional Linear Regression

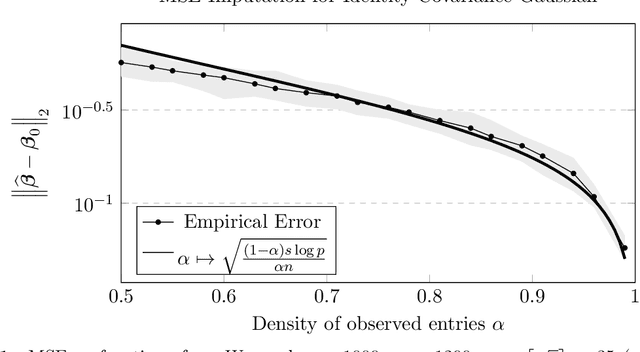
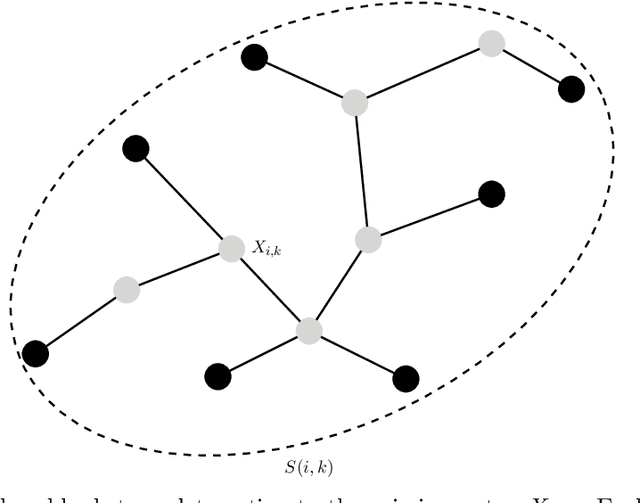
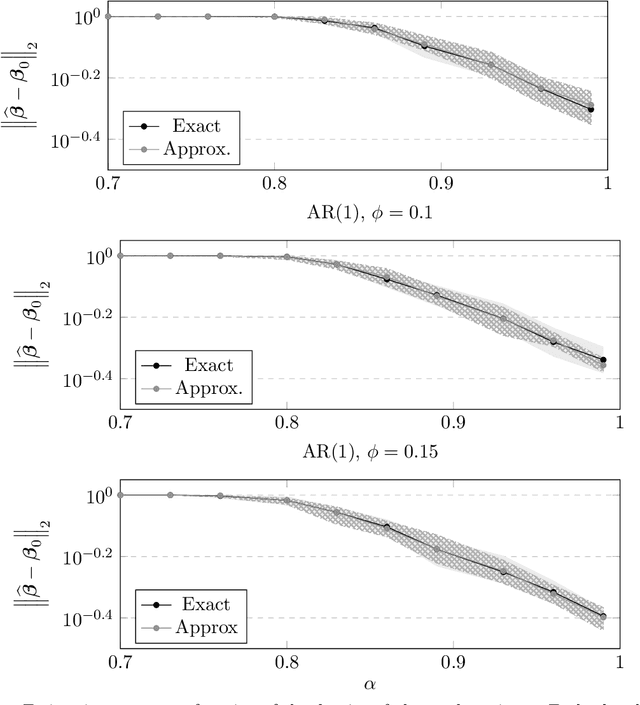
We study high-dimensional regression with missing entries in the covariates. A common strategy in practice is to \emph{impute} the missing entries with an appropriate substitute and then implement a standard statistical procedure acting as if the covariates were fully observed. Recent literature on this subject proposes instead to design a specific, often complicated or non-convex, algorithm tailored to the case of missing covariates. We investigate a simpler approach where we fill-in the missing entries with their conditional mean given the observed covariates. We show that this imputation scheme coupled with standard off-the-shelf procedures such as the LASSO and square-root LASSO retains the minimax estimation rate in the random-design setting where the covariates are i.i.d.\ sub-Gaussian. We further show that the square-root LASSO remains \emph{pivotal} in this setting. It is often the case that the conditional expectation cannot be computed exactly and must be approximated from data. We study two cases where the covariates either follow an autoregressive (AR) process, or are jointly Gaussian with sparse precision matrix. We propose tractable estimators for the conditional expectation and then perform linear regression via LASSO, and show similar estimation rates in both cases. We complement our theoretical results with simulations on synthetic and semi-synthetic examples, illustrating not only the sharpness of our bounds, but also the broader utility of this strategy beyond our theoretical assumptions.

The Kikuchi Hierarchy and Tensor PCA

For the tensor PCA (principal component analysis) problem, we propose a new hierarchy of algorithms that are increasingly powerful yet require increasing runtime. Our hierarchy is analogous to the sum-of-squares (SOS) hierarchy but is instead inspired by statistical physics and related algorithms such as belief propagation and AMP (approximate message passing). Our level-$\ell$ algorithm can be thought of as a (linearized) message-passing algorithm that keeps track of $\ell$-wise dependencies among the hidden variables. Specifically, our algorithms are spectral methods based on the Kikuchi Hessian matrix, which generalizes the well-studied Bethe Hessian matrix to the higher-order Kikuchi free energies. It is known that AMP, the flagship algorithm of statistical physics, has substantially worse performance than SOS for tensor PCA. In this work we `redeem' the statistical physics approach by showing that our hierarchy gives a polynomial-time algorithm matching the performance of SOS. Our hierarchy also yields a continuum of subexponential-time algorithms, and we prove that these achieve the same (conjecturally optimal) tradeoff between runtime and statistical power as SOS. Our results hold for even-order tensors, and we conjecture that they also hold for odd-order tensors. Our methods suggest a new avenue for systematically obtaining optimal algorithms for Bayesian inference problems, and our results constitute a step toward unifying the statistical physics and sum-of-squares approaches to algorithm design.

Fundamental limits of detection in the spiked Wigner model

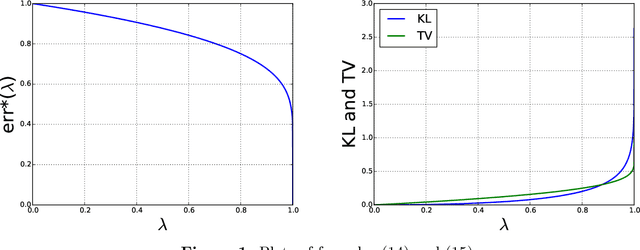
We study the fundamental limits of detecting the presence of an additive rank-one perturbation, or spike, to a Wigner matrix. When the spike comes from a prior that is i.i.d. across coordinates, we prove that the log-likelihood ratio of the spiked model against the non-spiked one is asymptotically normal below a certain reconstruction threshold which is not necessarily of a "spectral" nature, and that it is degenerate above. This establishes the maximal region of contiguity between the planted and null models. It is known that this threshold also marks a phase transition for estimating the spike: the latter task is possible above the threshold and impossible below. Therefore, both estimation and detection undergo the same transition in this random matrix model. We also provide further information about the performance of the optimal test. Our proofs are based on Gaussian interpolation methods and a rigorous incarnation of the cavity method, as devised by Guerra and Talagrand in their study of the Sherrington--Kirkpatrick spin-glass model.

Detection limits in the high-dimensional spiked rectangular model

We study the problem of detecting the presence of a single unknown spike in a rectangular data matrix, in a high-dimensional regime where the spike has fixed strength and the aspect ratio of the matrix converges to a finite limit. This setup includes Johnstone's spiked covariance model. We analyze the likelihood ratio of the spiked model against an "all noise" null model of reference, and show it has asymptotically Gaussian fluctuations in a region below---but in general not up to---the so-called BBP threshold from random matrix theory. Our result parallels earlier findings of Onatski et al.\ (2013) and Johnstone-Onatski (2015) for spherical spikes. We present a probabilistic approach capable of treating generic product priors. In particular, sparsity in the spike is allowed. Our approach is based on Talagrand's interpretation of the cavity method from spin-glass theory. The question of the maximal parameter region where asymptotic normality is expected to hold is left open. This region is shaped by the prior in a non-trivial way. We conjecture that this is the entire paramagnetic phase of an associated spin-glass model, and is defined by the vanishing of the replica-symmetric solution of Lesieur et al.\ (2015).

Tight Query Complexity Lower Bounds for PCA via Finite Sample Deformed Wigner Law

We prove a \emph{query complexity} lower bound for approximating the top $r$ dimensional eigenspace of a matrix. We consider an oracle model where, given a symmetric matrix $\mathbf{M} \in \mathbb{R}^{d \times d}$, an algorithm $\mathsf{Alg}$ is allowed to make $\mathsf{T}$ exact queries of the form $\mathsf{w}^{(i)} = \mathbf{M} \mathsf{v}^{(i)}$ for $i$ in $\{1,...,\mathsf{T}\}$, where $\mathsf{v}^{(i)}$ is drawn from a distribution which depends arbitrarily on the past queries and measurements $\{\mathsf{v}^{(j)},\mathsf{w}^{(i)}\}_{1 \le j \le i-1}$. We show that for every $\mathtt{gap} \in (0,1/2]$, there exists a distribution over matrices $\mathbf{M}$ for which 1) $\mathrm{gap}_r(\mathbf{M}) = \Omega(\mathtt{gap})$ (where $\mathrm{gap}_r(\mathbf{M})$ is the normalized gap between the $r$ and $r+1$-st largest-magnitude eigenvector of $\mathbf{M}$), and 2) any algorithm $\mathsf{Alg}$ which takes fewer than $\mathrm{const} \times \frac{r \log d}{\sqrt{\mathtt{gap}}}$ queries fails (with overwhelming probability) to identity a matrix $\widehat{\mathsf{V}} \in \mathbb{R}^{d \times r}$ with orthonormal columns for which $\langle \widehat{\mathsf{V}}, \mathbf{M} \widehat{\mathsf{V}}\rangle \ge (1 - \mathrm{const} \times \mathtt{gap})\sum_{i=1}^r \lambda_i(\mathbf{M})$. Our bound requires only that $d$ is a small polynomial in $1/\mathtt{gap}$ and $r$, and matches the upper bounds of Musco and Musco '15. Moreover, it establishes a strict separation between convex optimization and \emph{randomized}, "strict-saddle" non-convex optimization of which PCA is a canonical example: in the former, first-order methods can have dimension-free iteration complexity, whereas in PCA, the iteration complexity of gradient-based methods must necessarily grow with the dimension.

Asymptotic behavior of $\ell_p$-based Laplacian regularization in semi-supervised learning

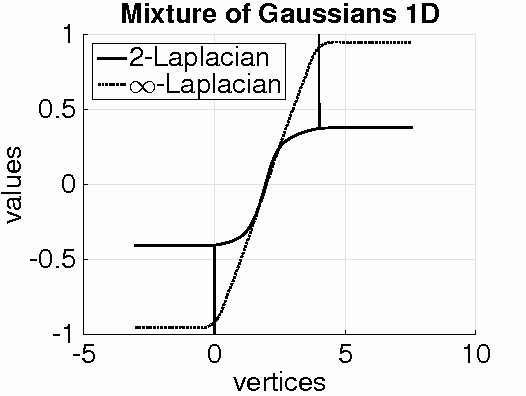
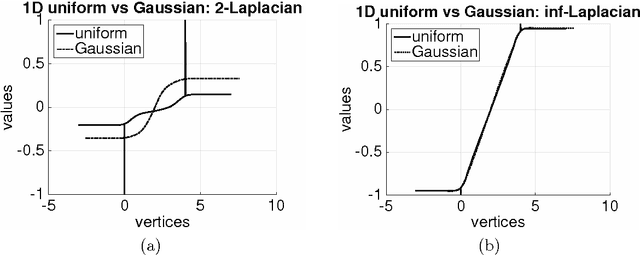
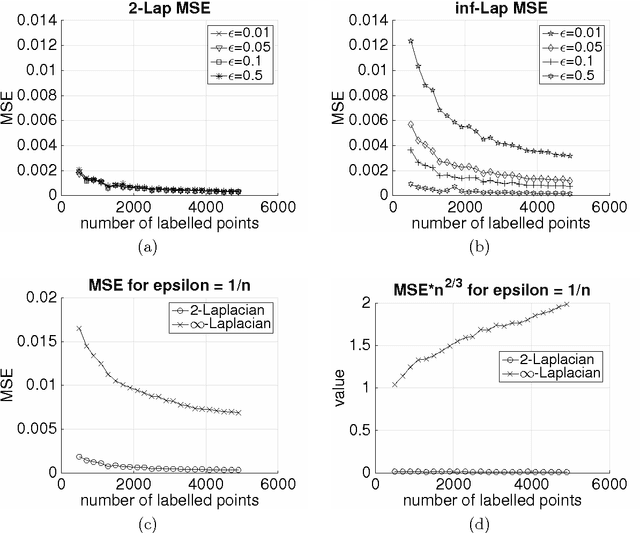
Given a weighted graph with $N$ vertices, consider a real-valued regression problem in a semi-supervised setting, where one observes $n$ labeled vertices, and the task is to label the remaining ones. We present a theoretical study of $\ell_p$-based Laplacian regularization under a $d$-dimensional geometric random graph model. We provide a variational characterization of the performance of this regularized learner as $N$ grows to infinity while $n$ stays constant, the associated optimality conditions lead to a partial differential equation that must be satisfied by the associated function estimate $\hat{f}$. From this formulation we derive several predictions on the limiting behavior the $d$-dimensional function $\hat{f}$, including (a) a phase transition in its smoothness at the threshold $p = d + 1$, and (b) a tradeoff between smoothness and sensitivity to the underlying unlabeled data distribution $P$. Thus, over the range $p \leq d$, the function estimate $\hat{f}$ is degenerate and "spiky," whereas for $p\geq d+1$, the function estimate $\hat{f}$ is smooth. We show that the effect of the underlying density vanishes monotonically with $p$, such that in the limit $p = \infty$, corresponding to the so-called Absolutely Minimal Lipschitz Extension, the estimate $\hat{f}$ is independent of the distribution $P$. Under the assumption of semi-supervised smoothness, ignoring $P$ can lead to poor statistical performance, in particular, we construct a specific example for $d=1$ to demonstrate that $p=2$ has lower risk than $p=\infty$ due to the former penalty adapting to $P$ and the latter ignoring it. We also provide simulations that verify the accuracy of our predictions for finite sample sizes. Together, these properties show that $p = d+1$ is an optimal choice, yielding a function estimate $\hat{f}$ that is both smooth and non-degenerate, while remaining maximally sensitive to $P$.

Fast Randomized Kernel Methods With Statistical Guarantees

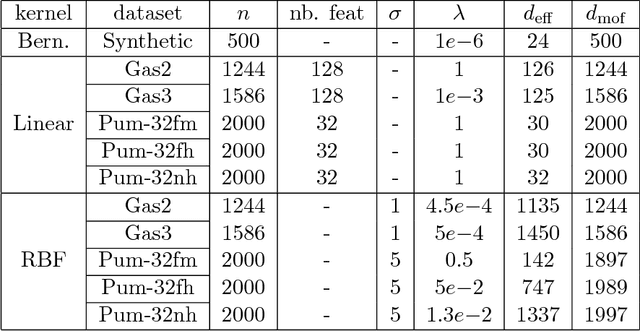
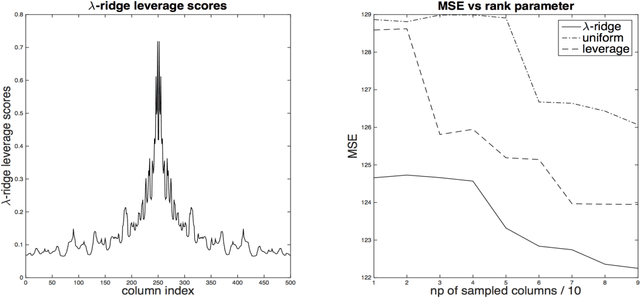
One approach to improving the running time of kernel-based machine learning methods is to build a small sketch of the input and use it in lieu of the full kernel matrix in the machine learning task of interest. Here, we describe a version of this approach that comes with running time guarantees as well as improved guarantees on its statistical performance. By extending the notion of \emph{statistical leverage scores} to the setting of kernel ridge regression, our main statistical result is to identify an importance sampling distribution that reduces the size of the sketch (i.e., the required number of columns to be sampled) to the \emph{effective dimensionality} of the problem. This quantity is often much smaller than previous bounds that depend on the \emph{maximal degrees of freedom}. Our main algorithmic result is to present a fast algorithm to compute approximations to these scores. This algorithm runs in time that is linear in the number of samples---more precisely, the running time is $O(np^2)$, where the parameter $p$ depends only on the trace of the kernel matrix and the regularization parameter---and it can be applied to the matrix of feature vectors, without having to form the full kernel matrix. This is obtained via a variant of length-squared sampling that we adapt to the kernel setting in a way that is of independent interest. Lastly, we provide empirical results illustrating our theory, and we discuss how this new notion of the statistical leverage of a data point captures in a fine way the difficulty of the original statistical learning problem.