Alternating minimization for generalized rank one matrix sensing: Sharp predictions from a random initialization

We consider the problem of estimating the factors of a rank-$1$ matrix with i.i.d. Gaussian, rank-$1$ measurements that are nonlinearly transformed and corrupted by noise. Considering two prototypical choices for the nonlinearity, we study the convergence properties of a natural alternating update rule for this nonconvex optimization problem starting from a random initialization. We show sharp convergence guarantees for a sample-split version of the algorithm by deriving a deterministic recursion that is accurate even in high-dimensional problems. Notably, while the infinite-sample population update is uninformative and suggests exact recovery in a single step, the algorithm -- and our deterministic prediction -- converges geometrically fast from a random initialization. Our sharp, non-asymptotic analysis also exposes several other fine-grained properties of this problem, including how the nonlinearity and noise level affect convergence behavior. On a technical level, our results are enabled by showing that the empirical error recursion can be predicted by our deterministic sequence within fluctuations of the order $n^{-1/2}$ when each iteration is run with $n$ observations. Our technique leverages leave-one-out tools originating in the literature on high-dimensional $M$-estimation and provides an avenue for sharply analyzing higher-order iterative algorithms from a random initialization in other high-dimensional optimization problems with random data.

Sharp global convergence guarantees for iterative nonconvex optimization: A Gaussian process perspective

We consider a general class of regression models with normally distributed covariates, and the associated nonconvex problem of fitting these models from data. We develop a general recipe for analyzing the convergence of iterative algorithms for this task from a random initialization. In particular, provided each iteration can be written as the solution to a convex optimization problem satisfying some natural conditions, we leverage Gaussian comparison theorems to derive a deterministic sequence that provides sharp upper and lower bounds on the error of the algorithm with sample-splitting. Crucially, this deterministic sequence accurately captures both the convergence rate of the algorithm and the eventual error floor in the finite-sample regime, and is distinct from the commonly used "population" sequence that results from taking the infinite-sample limit. We apply our general framework to derive several concrete consequences for parameter estimation in popular statistical models including phase retrieval and mixtures of regressions. Provided the sample size scales near-linearly in the dimension, we show sharp global convergence rates for both higher-order algorithms based on alternating updates and first-order algorithms based on subgradient descent. These corollaries, in turn, yield multiple consequences, including: (a) Proof that higher-order algorithms can converge significantly faster than their first-order counterparts (and sometimes super-linearly), even if the two share the same population update and (b) Intricacies in super-linear convergence behavior for higher-order algorithms, which can be nonstandard (e.g., with exponent 3/2) and sensitive to the noise level in the problem. We complement these results with extensive numerical experiments, which show excellent agreement with our theoretical predictions.

Imputation for High-Dimensional Linear Regression

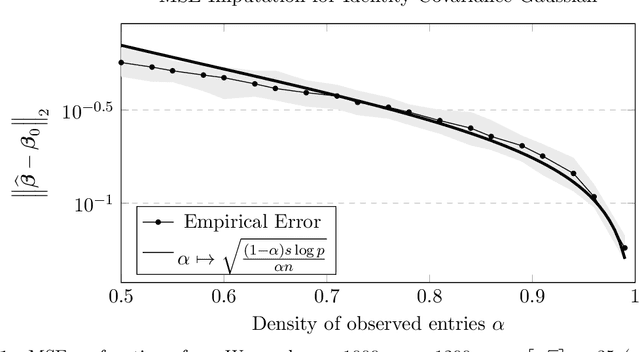
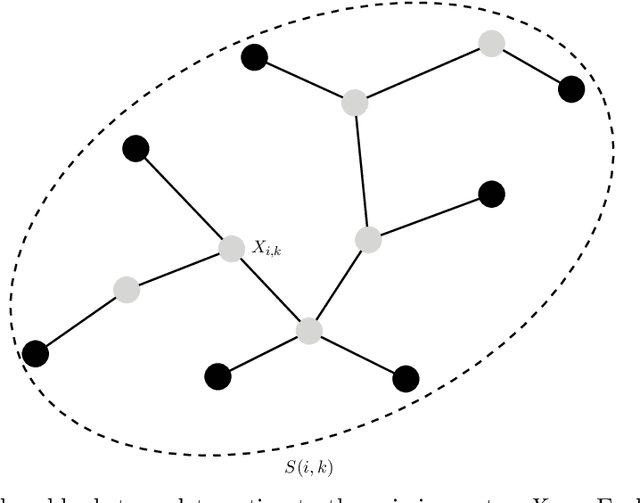
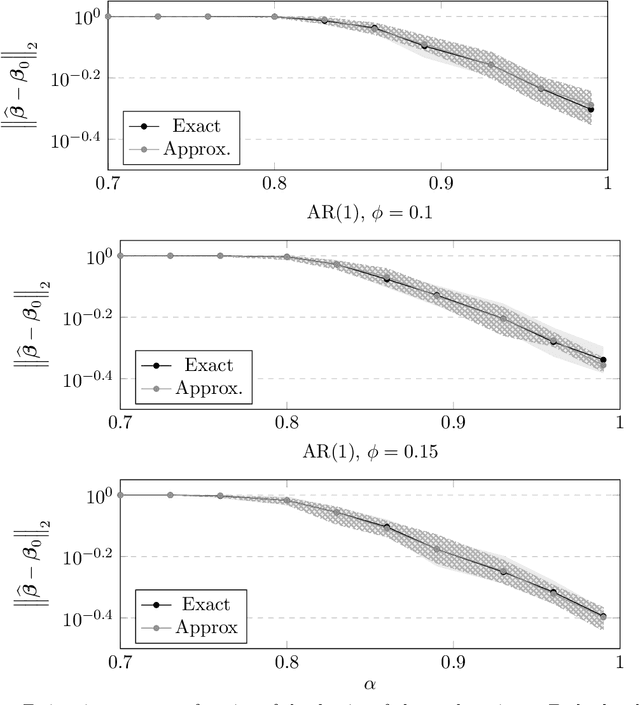
We study high-dimensional regression with missing entries in the covariates. A common strategy in practice is to \emph{impute} the missing entries with an appropriate substitute and then implement a standard statistical procedure acting as if the covariates were fully observed. Recent literature on this subject proposes instead to design a specific, often complicated or non-convex, algorithm tailored to the case of missing covariates. We investigate a simpler approach where we fill-in the missing entries with their conditional mean given the observed covariates. We show that this imputation scheme coupled with standard off-the-shelf procedures such as the LASSO and square-root LASSO retains the minimax estimation rate in the random-design setting where the covariates are i.i.d.\ sub-Gaussian. We further show that the square-root LASSO remains \emph{pivotal} in this setting. It is often the case that the conditional expectation cannot be computed exactly and must be approximated from data. We study two cases where the covariates either follow an autoregressive (AR) process, or are jointly Gaussian with sparse precision matrix. We propose tractable estimators for the conditional expectation and then perform linear regression via LASSO, and show similar estimation rates in both cases. We complement our theoretical results with simulations on synthetic and semi-synthetic examples, illustrating not only the sharpness of our bounds, but also the broader utility of this strategy beyond our theoretical assumptions.