Perfusion Imaging and Single Material Reconstruction in Polychromatic Photon Counting CT

Background: Perfusion computed tomography (CT) images the dynamics of a contrast agent through the body over time, and is one of the highest X-ray dose scans in medical imaging. Recently, a theoretically justified reconstruction algorithm based on a monotone variational inequality (VI) was proposed for single material polychromatic photon-counting CT, and showed promising early results at low-dose imaging. Purpose: We adapt this reconstruction algorithm for perfusion CT, to reconstruct the concentration map of the contrast agent while the static background tissue is assumed known; we call our method VI-PRISM (VI-based PeRfusion Imaging and Single Material reconstruction). We evaluate its potential for dose-reduced perfusion CT, using a digital phantom with water and iodine of varying concentration. Methods: Simulated iodine concentrations range from 0.05 to 2.5 mg/ml. The simulated X-ray source emits photons up to 100 keV, with average intensity ranging from $10^5$ down to $10^2$ photons per detector element. The number of tomographic projections was varied from 984 down to 8 to characterize the tradeoff in photon allocation between views and intensity. Results: We compare VI-PRISM against filtered back-projection (FBP), and find that VI-PRISM recovers iodine concentration with error below 0.4 mg/ml at all source intensity levels tested. Even with a dose reduction between 10x and 100x compared to FBP, VI-PRISM exhibits reconstruction quality on par with FBP. Conclusion: Across all photon budgets and angular sampling densities tested, VI-PRISM achieved consistently lower RMSE, reduced noise, and higher SNR compared to filtered back-projection. Even in extremely photon-limited and sparsely sampled regimes, VI-PRISM recovered iodine concentrations with errors below 0.4 mg/ml, showing that VI-PRISM can support accurate and dose-efficient perfusion imaging in photon-counting CT.

Multiscale replay: A robust algorithm for stochastic variational inequalities with a Markovian buffer

We introduce the Multiscale Experience Replay (MER) algorithm for solving a class of stochastic variational inequalities (VIs) in settings where samples are generated from a Markov chain and we have access to a memory buffer to store them. Rather than uniformly sampling from the buffer, MER utilizes a multi-scale sampling scheme to emulate the behavior of VI algorithms designed for independent and identically distributed samples, overcoming bias in the de facto serial scheme and thereby accelerating convergence. Notably, unlike standard sample-skipping variants of serial algorithms, MER is robust in that it achieves this acceleration in iteration complexity whenever possible, and without requiring knowledge of the mixing time of the Markov chain. We also discuss applications of MER, particularly in policy evaluation with temporal difference learning and in training generalized linear models with dependent data.

Efficient reductions from a Gaussian source with applications to statistical-computational tradeoffs

Given a single observation from a Gaussian distribution with unknown mean $\theta$, we design computationally efficient procedures that can approximately generate an observation from a different target distribution $Q_{\theta}$ uniformly for all $\theta$ in a parameter set. We leverage our technique to establish reduction-based computational lower bounds for several canonical high-dimensional statistical models under widely-believed conjectures in average-case complexity. In particular, we cover cases in which: 1. $Q_{\theta}$ is a general location model with non-Gaussian distribution, including both light-tailed examples (e.g., generalized normal distributions) and heavy-tailed ones (e.g., Student's $t$-distributions). As a consequence, we show that computational lower bounds proved for spiked tensor PCA with Gaussian noise are universal, in that they extend to other non-Gaussian noise distributions within our class. 2. $Q_{\theta}$ is a normal distribution with mean $f(\theta)$ for a general, smooth, and nonlinear link function $f:\mathbb{R} \rightarrow \mathbb{R}$. Using this reduction, we construct a reduction from symmetric mixtures of linear regressions to generalized linear models with link function $f$, and establish computational lower bounds for solving the $k$-sparse generalized linear model when $f$ is an even function. This result constitutes the first reduction-based confirmation of a $k$-to-$k^2$ statistical-to-computational gap in $k$-sparse phase retrieval, resolving a conjecture posed by Cai et al. (2016). As a second application, we construct a reduction from the sparse rank-1 submatrix model to the planted submatrix model, establishing a pointwise correspondence between the phase diagrams of the two models that faithfully preserves regions of computational hardness and tractability.

Estimating stationary mass, frequency by frequency

Suppose we observe a trajectory of length $n$ from an $\alpha$-mixing stochastic process over a finite but potentially large state space. We consider the problem of estimating the probability mass placed by the stationary distribution of any such process on elements that occur with a certain frequency in the observed sequence. We estimate this vector of probabilities in total variation distance, showing universal consistency in $n$ and recovering known results for i.i.d. sequences as special cases. Our proposed methodology carefully combines the plug-in (or empirical) estimator with a recently-proposed modification of the Good--Turing estimator called \textsc{WingIt}, which was originally developed for Markovian sequences. En route to controlling the error of our estimator, we develop new performance bounds on \textsc{WingIt} and the plug-in estimator for $\alpha$-mixing stochastic processes. Importantly, the extensively used method of Poissonization can no longer be applied in our non i.i.d. setting, and so we develop complementary tools -- including concentration inequalities for a natural self-normalized statistic of mixing sequences -- that may prove independently useful in the design and analysis of estimators for related problems.

Just Wing It: Optimal Estimation of Missing Mass in a Markovian Sequence

We study the problem of estimating the stationary mass -- also called the unigram mass -- that is missing from a single trajectory of a discrete-time, ergodic Markov chain. This problem has several applications -- for example, estimating the stationary missing mass is critical for accurately smoothing probability estimates in sequence models. While the classical Good--Turing estimator from the 1950s has appealing properties for i.i.d. data, it is known to be biased in the Markov setting, and other heuristic estimators do not come equipped with guarantees. Operating in the general setting in which the size of the state space may be much larger than the length $n$ of the trajectory, we develop a linear-runtime estimator called \emph{Windowed Good--Turing} (\textsc{WingIt}) and show that its risk decays as $\widetilde{\mathcal{O}}(\mathsf{T_{mix}}/n)$, where $\mathsf{T_{mix}}$ denotes the mixing time of the chain in total variation distance. Notably, this rate is independent of the size of the state space and minimax-optimal up to a logarithmic factor in $n / \mathsf{T_{mix}}$. We also present a bound on the variance of the missing mass random variable, which may be of independent interest. We extend our estimator to approximate the stationary mass placed on elements occurring with small frequency in $X^n$. Finally, we demonstrate the efficacy of our estimators both in simulations on canonical chains and on sequences constructed from a popular natural language corpus.

Efficient reductions between some statistical models

We study the problem of approximately transforming a sample from a source statistical model to a sample from a target statistical model without knowing the parameters of the source model, and construct several computationally efficient such reductions between statistical experiments. In particular, we provide computationally efficient procedures that approximately reduce uniform, Erlang, and Laplace location models to general target families. We illustrate our methodology by establishing nonasymptotic reductions between some canonical high-dimensional problems, spanning mixtures of experts, phase retrieval, and signal denoising. Notably, the reductions are structure preserving and can accommodate missing data. We also point to a possible application in transforming one differentially private mechanism to another.

Hyperparameter tuning via trajectory predictions: Stochastic prox-linear methods in matrix sensing

Motivated by the desire to understand stochastic algorithms for nonconvex optimization that are robust to their hyperparameter choices, we analyze a mini-batched prox-linear iterative algorithm for the problem of recovering an unknown rank-1 matrix from rank-1 Gaussian measurements corrupted by noise. We derive a deterministic recursion that predicts the error of this method and show, using a non-asymptotic framework, that this prediction is accurate for any batch-size and a large range of step-sizes. In particular, our analysis reveals that this method, though stochastic, converges linearly from a local initialization with a fixed step-size to a statistical error floor. Our analysis also exposes how the batch-size, step-size, and noise level affect the (linear) convergence rate and the eventual statistical estimation error, and we demonstrate how to use our deterministic predictions to perform hyperparameter tuning (e.g. step-size and batch-size selection) without ever running the method. On a technical level, our analysis is enabled in part by showing that the fluctuations of the empirical iterates around our deterministic predictions scale with the error of the previous iterate.

Perceptual adjustment queries and an inverted measurement paradigm for low-rank metric learning

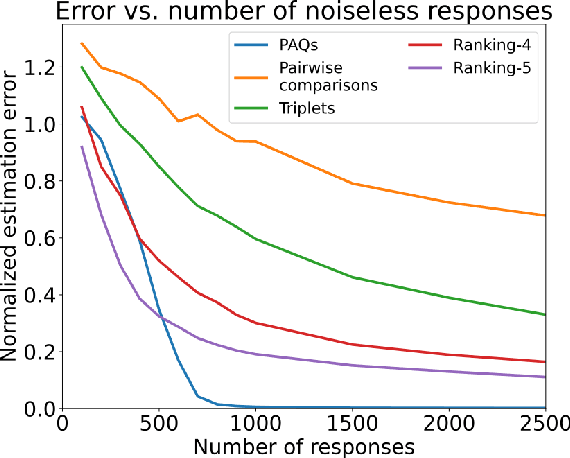
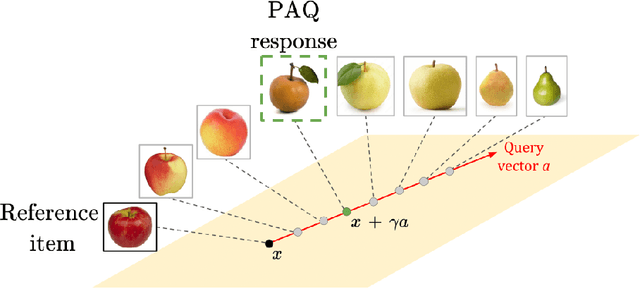
We introduce a new type of query mechanism for collecting human feedback, called the perceptual adjustment query ( PAQ). Being both informative and cognitively lightweight, the PAQ adopts an inverted measurement scheme, and combines advantages from both cardinal and ordinal queries. We showcase the PAQ in the metric learning problem, where we collect PAQ measurements to learn an unknown Mahalanobis distance. This gives rise to a high-dimensional, low-rank matrix estimation problem to which standard matrix estimators cannot be applied. Consequently, we develop a two-stage estimator for metric learning from PAQs, and provide sample complexity guarantees for this estimator. We present numerical simulations demonstrating the performance of the estimator and its notable properties.

Do algorithms and barriers for sparse principal component analysis extend to other structured settings?

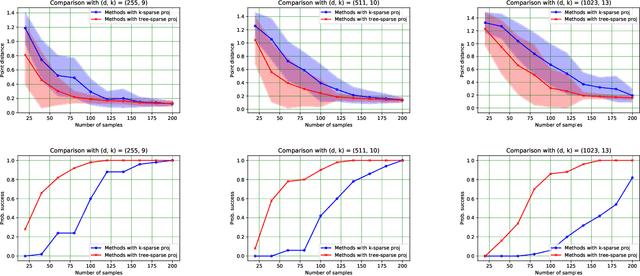
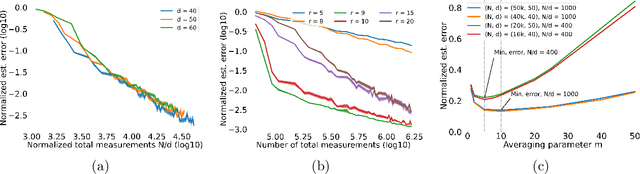
We study a principal component analysis problem under the spiked Wishart model in which the structure in the signal is captured by a class of union-of-subspace models. This general class includes vanilla sparse PCA as well as its variants with graph sparsity. With the goal of studying these problems under a unified statistical and computational lens, we establish fundamental limits that depend on the geometry of the problem instance, and show that a natural projected power method exhibits local convergence to the statistically near-optimal neighborhood of the solution. We complement these results with end-to-end analyses of two important special cases given by path and tree sparsity in a general basis, showing initialization methods and matching evidence of computational hardness. Overall, our results indicate that several of the phenomena observed for vanilla sparse PCA extend in a natural fashion to its structured counterparts.

Sharp analysis of EM for learning mixtures of pairwise differences

We consider a symmetric mixture of linear regressions with random samples from the pairwise comparison design, which can be seen as a noisy version of a type of Euclidean distance geometry problem. We analyze the expectation-maximization (EM) algorithm locally around the ground truth and establish that the sequence converges linearly, providing an $\ell_\infty$-norm guarantee on the estimation error of the iterates. Furthermore, we show that the limit of the EM sequence achieves the sharp rate of estimation in the $\ell_2$-norm, matching the information-theoretically optimal constant. We also argue through simulation that convergence from a random initialization is much more delicate in this setting, and does not appear to occur in general. Our results show that the EM algorithm can exhibit several unique behaviors when the covariate distribution is suitably structured.