Impossibility of latent inner product recovery via rate distortion

In this largely expository note, we present an impossibility result for inner product recovery in a random geometric graph or latent space model using the rate-distortion theory. More precisely, suppose that we observe a graph $A$ on $n$ vertices with average edge density $p$ generated from Gaussian or spherical latent locations $z_1, \dots, z_n \in \mathbb{R}^d$ associated with the $n$ vertices. It is of interest to estimate the inner products $\langle z_i, z_j \rangle$ which represent the geometry of the latent points. We prove that it is impossible to recover the inner products if $d \gtrsim n h(p)$ where $h(p)$ is the binary entropy function. This matches the condition required for positive results on inner product recovery in the literature. The proof follows the well-established rate-distortion theory with the main technical ingredient being a lower bound on the rate-distortion function of the Wishart distribution which is interesting in its own right.

Information-Theoretic Thresholds for Planted Dense Cycles

We study a random graph model for small-world networks which are ubiquitous in social and biological sciences. In this model, a dense cycle of expected bandwidth $n \tau$, representing the hidden one-dimensional geometry of vertices, is planted in an ambient random graph on $n$ vertices. For both detection and recovery of the planted dense cycle, we characterize the information-theoretic thresholds in terms of $n$, $\tau$, and an edge-wise signal-to-noise ratio $\lambda$. In particular, the information-theoretic thresholds differ from the computational thresholds established in a recent work for low-degree polynomial algorithms, thereby justifying the existence of statistical-to-computational gaps for this problem.

Detection of Dense Subhypergraphs by Low-Degree Polynomials

Detection of a planted dense subgraph in a random graph is a fundamental statistical and computational problem that has been extensively studied in recent years. We study a hypergraph version of the problem. Let $G^r(n,p)$ denote the $r$-uniform Erd\H{o}s-R\'enyi hypergraph model with $n$ vertices and edge density $p$. We consider detecting the presence of a planted $G^r(n^\gamma, n^{-\alpha})$ subhypergraph in a $G^r(n, n^{-\beta})$ hypergraph, where $0< \alpha < \beta < r-1$ and $0 < \gamma < 1$. Focusing on tests that are degree-$n^{o(1)}$ polynomials of the entries of the adjacency tensor, we determine the threshold between the easy and hard regimes for the detection problem. More precisely, for $0 < \gamma < 1/2$, the threshold is given by $\alpha = \beta \gamma$, and for $1/2 \le \gamma < 1$, the threshold is given by $\alpha = \beta/2 + r(\gamma - 1/2)$. Our results are already new in the graph case $r=2$, as we consider the subtle log-density regime where hardness based on average-case reductions is not known. Our proof of low-degree hardness is based on a conditional variant of the standard low-degree likelihood calculation.

Sharp analysis of EM for learning mixtures of pairwise differences

We consider a symmetric mixture of linear regressions with random samples from the pairwise comparison design, which can be seen as a noisy version of a type of Euclidean distance geometry problem. We analyze the expectation-maximization (EM) algorithm locally around the ground truth and establish that the sequence converges linearly, providing an $\ell_\infty$-norm guarantee on the estimation error of the iterates. Furthermore, we show that the limit of the EM sequence achieves the sharp rate of estimation in the $\ell_2$-norm, matching the information-theoretically optimal constant. We also argue through simulation that convergence from a random initialization is much more delicate in this setting, and does not appear to occur in general. Our results show that the EM algorithm can exhibit several unique behaviors when the covariate distribution is suitably structured.

Detection-Recovery Gap for Planted Dense Cycles

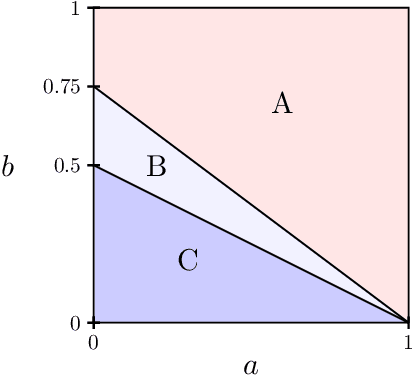
Planted dense cycles are a type of latent structure that appears in many applications, such as small-world networks in social sciences and sequence assembly in computational biology. We consider a model where a dense cycle with expected bandwidth $n \tau$ and edge density $p$ is planted in an Erd\H{o}s-R\'enyi graph $G(n,q)$. We characterize the computational thresholds for the associated detection and recovery problems for the class of low-degree polynomial algorithms. In particular, a gap exists between the two thresholds in a certain regime of parameters. For example, if $n^{-3/4} \ll \tau \ll n^{-1/2}$ and $p = C q = \Theta(1)$ for a constant $C>1$, the detection problem is computationally easy while the recovery problem is hard for low-degree algorithms.

Random graph matching at Otter's threshold via counting chandeliers

We propose an efficient algorithm for graph matching based on similarity scores constructed from counting a certain family of weighted trees rooted at each vertex. For two Erd\H{o}s-R\'enyi graphs $\mathcal{G}(n,q)$ whose edges are correlated through a latent vertex correspondence, we show that this algorithm correctly matches all but a vanishing fraction of the vertices with high probability, provided that $nq\to\infty$ and the edge correlation coefficient $\rho$ satisfies $\rho^2>\alpha \approx 0.338$, where $\alpha$ is Otter's tree-counting constant. Moreover, this almost exact matching can be made exact under an extra condition that is information-theoretically necessary. This is the first polynomial-time graph matching algorithm that succeeds at an explicit constant correlation and applies to both sparse and dense graphs. In comparison, previous methods either require $\rho=1-o(1)$ or are restricted to sparse graphs. The crux of the algorithm is a carefully curated family of rooted trees called chandeliers, which allows effective extraction of the graph correlation from the counts of the same tree while suppressing the undesirable correlation between those of different trees.

Testing network correlation efficiently via counting trees

We propose a new procedure for testing whether two networks are edge-correlated through some latent vertex correspondence. The test statistic is based on counting the co-occurrences of signed trees for a family of non-isomorphic trees. When the two networks are Erd\H{o}s-R\'enyi random graphs $\mathcal{G}(n,q)$ that are either independent or correlated with correlation coefficient $\rho$, our test runs in $n^{2+o(1)}$ time and succeeds with high probability as $n\to\infty$, provided that $n\min\{q,1-q\} \ge n^{-o(1)}$ and $\rho^2>\alpha \approx 0.338$, where $\alpha$ is Otter's constant so that the number of unlabeled trees with $K$ edges grows as $(1/\alpha)^K$. This significantly improves the prior work in terms of statistical accuracy, running time, and graph sparsity.

Exact Matching of Random Graphs with Constant Correlation

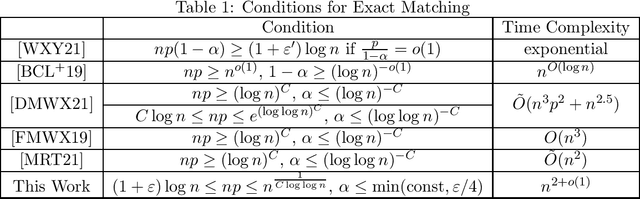
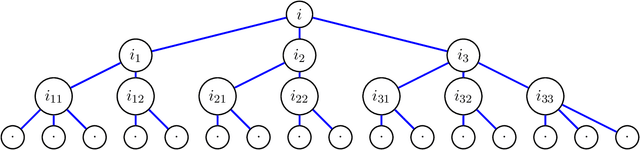
This paper deals with the problem of graph matching or network alignment for Erd\H{o}s--R\'enyi graphs, which can be viewed as a noisy average-case version of the graph isomorphism problem. Let $G$ and $G'$ be $G(n, p)$ Erd\H{o}s--R\'enyi graphs marginally, identified with their adjacency matrices. Assume that $G$ and $G'$ are correlated such that $\mathbb{E}[G_{ij} G'_{ij}] = p(1-\alpha)$. For a permutation $\pi$ representing a latent matching between the vertices of $G$ and $G'$, denote by $G^\pi$ the graph obtained from permuting the vertices of $G$ by $\pi$. Observing $G^\pi$ and $G'$, we aim to recover the matching $\pi$. In this work, we show that for every $\varepsilon \in (0,1]$, there is $n_0>0$ depending on $\varepsilon$ and absolute constants $\alpha_0, R > 0$ with the following property. Let $n \ge n_0$, $(1+\varepsilon) \log n \le np \le n^{\frac{1}{R \log \log n}}$, and $0 < \alpha < \min(\alpha_0,\varepsilon/4)$. There is a polynomial-time algorithm $F$ such that $\mathbb{P}\{F(G^\pi,G')=\pi\}=1-o(1)$. This is the first polynomial-time algorithm that recovers the exact matching between vertices of correlated Erd\H{o}s--R\'enyi graphs with constant correlation with high probability. The algorithm is based on comparison of partition trees associated with the graph vertices.

Optimal Spectral Recovery of a Planted Vector in a Subspace

Recovering a planted vector $v$ in an $n$-dimensional random subspace of $\mathbb{R}^N$ is a generic task related to many problems in machine learning and statistics, such as dictionary learning, subspace recovery, and principal component analysis. In this work, we study computationally efficient estimation and detection of a planted vector $v$ whose $\ell_4$ norm differs from that of a Gaussian vector with the same $\ell_2$ norm. For instance, in the special case of an $N \rho$-sparse vector $v$ with Rademacher nonzero entries, our results include the following: (1) We give an improved analysis of (a slight variant of) the spectral method proposed by Hopkins, Schramm, Shi, and Steurer, showing that it approximately recovers $v$ with high probability in the regime $n \rho \ll \sqrt{N}$. In contrast, previous work required either $\rho \ll 1/\sqrt{n}$ or $n \sqrt{\rho} \lesssim \sqrt{N}$ for polynomial-time recovery. Our result subsumes both of these conditions (up to logarithmic factors) and also treats the dense case $\rho = 1$ which was not previously considered. (2) Akin to $\ell_\infty$ bounds for eigenvector perturbation, we establish an entrywise error bound for the spectral estimator via a leave-one-out analysis, from which it follows that thresholding recovers $v$ exactly. (3) We study the associated detection problem and show that in the regime $n \rho \gg \sqrt{N}$, any spectral method from a large class (and more generally, any low-degree polynomial of the input) fails to detect the planted vector. This establishes optimality of our upper bounds and offers evidence that no polynomial-time algorithm can succeed when $n \rho \gg \sqrt{N}$.

Random Graph Matching with Improved Noise Robustness

Graph matching, also known as network alignment, refers to finding a bijection between the vertex sets of two given graphs so as to maximally align their edges. This fundamental computational problem arises frequently in multiple fields such as computer vision and biology. Recently, there has been a plethora of work studying efficient algorithms for graph matching under probabilistic models. In this work, we propose a new algorithm for graph matching and show that, for two Erd\H{o}s-R\'enyi graphs with edge correlation $1-\alpha$, our algorithm recovers the underlying matching with high probability when $\alpha \le 1 / (\log \log n)^C$, where $n$ is the number of vertices in each graph and $C$ denotes a positive universal constant. This improves the condition $\alpha \le 1 / (\log n)^C$ achieved in previous work.