Optimal Embedding Dimension for Sparse Subspace Embeddings

A random $m\times n$ matrix $S$ is an oblivious subspace embedding (OSE) with parameters $\epsilon>0$, $\delta\in(0,1/3)$ and $d\leq m\leq n$, if for any $d$-dimensional subspace $W\subseteq R^n$, $P\big(\,\forall_{x\in W}\ (1+\epsilon)^{-1}\|x\|\leq\|Sx\|\leq (1+\epsilon)\|x\|\,\big)\geq 1-\delta.$ It is known that the embedding dimension of an OSE must satisfy $m\geq d$, and for any $\theta > 0$, a Gaussian embedding matrix with $m\geq (1+\theta) d$ is an OSE with $\epsilon = O_\theta(1)$. However, such optimal embedding dimension is not known for other embeddings. Of particular interest are sparse OSEs, having $s\ll m$ non-zeros per column, with applications to problems such as least squares regression and low-rank approximation. We show that, given any $\theta > 0$, an $m\times n$ random matrix $S$ with $m\geq (1+\theta)d$ consisting of randomly sparsified $\pm1/\sqrt s$ entries and having $s= O(\log^4(d))$ non-zeros per column, is an oblivious subspace embedding with $\epsilon = O_{\theta}(1)$. Our result addresses the main open question posed by Nelson and Nguyen (FOCS 2013), who conjectured that sparse OSEs can achieve $m=O(d)$ embedding dimension, and it improves on $m=O(d\log(d))$ shown by Cohen (SODA 2016). We use this to construct the first oblivious subspace embedding with $O(d)$ embedding dimension that can be applied faster than current matrix multiplication time, and to obtain an optimal single-pass algorithm for least squares regression. We further extend our results to construct even sparser non-oblivious embeddings, leading to the first subspace embedding with low distortion $\epsilon=o(1)$ and optimal embedding dimension $m=O(d/\epsilon^2)$ that can be applied in current matrix multiplication time.

Exact Matching of Random Graphs with Constant Correlation

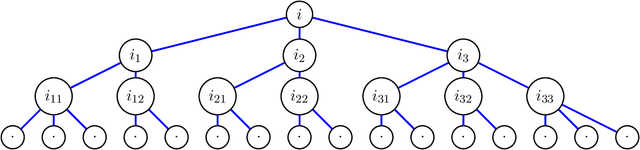
This paper deals with the problem of graph matching or network alignment for Erd\H{o}s--R\'enyi graphs, which can be viewed as a noisy average-case version of the graph isomorphism problem. Let $G$ and $G'$ be $G(n, p)$ Erd\H{o}s--R\'enyi graphs marginally, identified with their adjacency matrices. Assume that $G$ and $G'$ are correlated such that $\mathbb{E}[G_{ij} G'_{ij}] = p(1-\alpha)$. For a permutation $\pi$ representing a latent matching between the vertices of $G$ and $G'$, denote by $G^\pi$ the graph obtained from permuting the vertices of $G$ by $\pi$. Observing $G^\pi$ and $G'$, we aim to recover the matching $\pi$. In this work, we show that for every $\varepsilon \in (0,1]$, there is $n_0>0$ depending on $\varepsilon$ and absolute constants $\alpha_0, R > 0$ with the following property. Let $n \ge n_0$, $(1+\varepsilon) \log n \le np \le n^{\frac{1}{R \log \log n}}$, and $0 < \alpha < \min(\alpha_0,\varepsilon/4)$. There is a polynomial-time algorithm $F$ such that $\mathbb{P}\{F(G^\pi,G')=\pi\}=1-o(1)$. This is the first polynomial-time algorithm that recovers the exact matching between vertices of correlated Erd\H{o}s--R\'enyi graphs with constant correlation with high probability. The algorithm is based on comparison of partition trees associated with the graph vertices.

Random Graph Matching with Improved Noise Robustness

Graph matching, also known as network alignment, refers to finding a bijection between the vertex sets of two given graphs so as to maximally align their edges. This fundamental computational problem arises frequently in multiple fields such as computer vision and biology. Recently, there has been a plethora of work studying efficient algorithms for graph matching under probabilistic models. In this work, we propose a new algorithm for graph matching and show that, for two Erd\H{o}s-R\'enyi graphs with edge correlation $1-\alpha$, our algorithm recovers the underlying matching with high probability when $\alpha \le 1 / (\log \log n)^C$, where $n$ is the number of vertices in each graph and $C$ denotes a positive universal constant. This improves the condition $\alpha \le 1 / (\log n)^C$ achieved in previous work.

Restricted Isometry Property under High Correlations

Matrices satisfying the Restricted Isometry Property (RIP) play an important role in the areas of compressed sensing and statistical learning. RIP matrices with optimal parameters are mainly obtained via probabilistic arguments, as explicit constructions seem hard. It is therefore interesting to ask whether a fixed matrix can be incorporated into a construction of restricted isometries. In this paper, we construct a new broad ensemble of random matrices with dependent entries that satisfy the restricted isometry property. Our construction starts with a fixed (deterministic) matrix $X$ satisfying some simple stable rank condition, and we show that the matrix $XR$, where $R$ is a random matrix drawn from various popular probabilistic models (including, subgaussian, sparse, low-randomness, satisfying convex concentration property), satisfies the RIP with high probability. These theorems have various applications in signal recovery, random matrix theory, dimensionality reduction, etc. Additionally, motivated by an application for understanding the effectiveness of word vector embeddings popular in natural language processing and machine learning applications, we investigate the RIP of the matrix $XR^{(l)}$ where $R^{(l)}$ is formed by taking all possible (disregarding order) $l$-way entrywise products of the columns of a random matrix $R$.

Restricted Eigenvalue from Stable Rank with Applications to Sparse Linear Regression

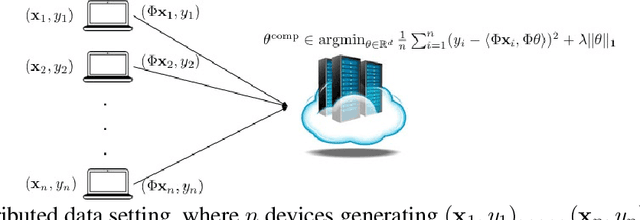
High-dimensional settings, where the data dimension ($d$) far exceeds the number of observations ($n$), are common in many statistical and machine learning applications. Methods based on $\ell_1$-relaxation, such as Lasso, are very popular for sparse recovery in these settings. Restricted Eigenvalue (RE) condition is among the weakest, and hence the most general, condition in literature imposed on the Gram matrix that guarantees nice statistical properties for the Lasso estimator. It is natural to ask: what families of matrices satisfy the RE condition? Following a line of work in this area, we construct a new broad ensemble of dependent random design matrices that have an explicit RE bound. Our construction starts with a fixed (deterministic) matrix $X \in \mathbb{R}^{n \times d}$ satisfying a simple stable rank condition, and we show that a matrix drawn from the distribution $X \Phi^\top \Phi$, where $\Phi \in \mathbb{R}^{m \times d}$ is a subgaussian random matrix, with high probability, satisfies the RE condition. This construction allows incorporating a fixed matrix that has an easily {\em verifiable} condition into the design process, and allows for generation of {\em compressed} design matrices that have a lower storage requirement than a standard design matrix. We give two applications of this construction to sparse linear regression problems, including one to a compressed sparse regression setting where the regression algorithm only has access to a compressed representation of a fixed design matrix $X$.

Errors-in-variables models with dependent measurements

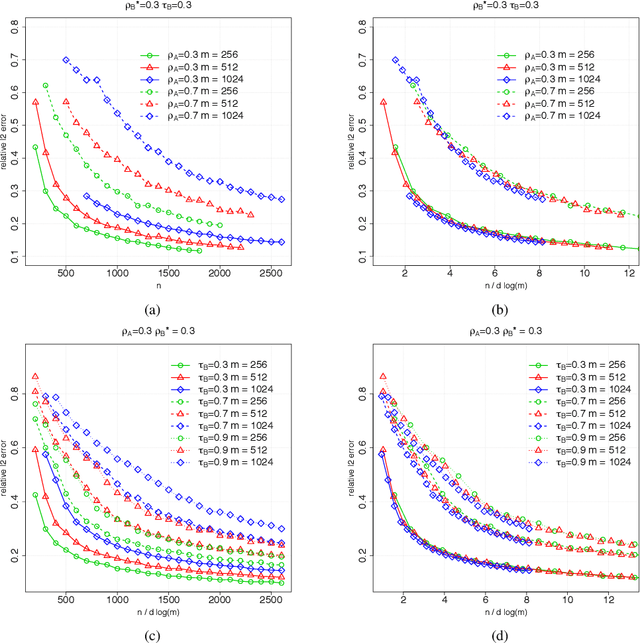
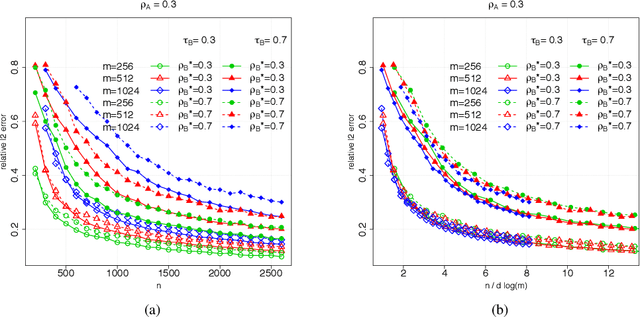
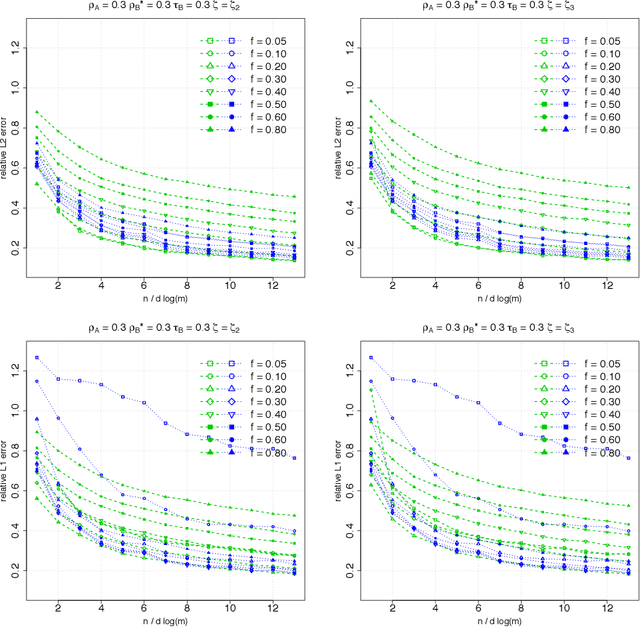
Suppose that we observe $y \in \mathbb{R}^n$ and $X \in \mathbb{R}^{n \times m}$ in the following errors-in-variables model: \begin{eqnarray*} y & = & X_0 \beta^* +\epsilon \\ X & = & X_0 + W, \end{eqnarray*} where $X_0$ is an $n \times m$ design matrix with independent subgaussian row vectors, $\epsilon \in \mathbb{R}^n$ is a noise vector and $W$ is a mean zero $n \times m$ random noise matrix with independent subgaussian column vectors, independent of $X_0$ and $\epsilon$. This model is significantly different from those analyzed in the literature in the sense that we allow the measurement error for each covariate to be a dependent vector across its $n$ observations. Such error structures appear in the science literature when modeling the trial-to-trial fluctuations in response strength shared across a set of neurons. Under sparsity and restrictive eigenvalue type of conditions, we show that one is able to recover a sparse vector $\beta^* \in \mathbb{R}^m$ from the model given a single observation matrix $X$ and the response vector $y$. We establish consistency in estimating $\beta^*$ and obtain the rates of convergence in the $\ell_q$ norm, where $q = 1, 2$. We show error bounds which approach that of the regular Lasso and the Dantzig selector in case the errors in $W$ are tending to 0. We analyze the convergence rates of the gradient descent methods for solving the nonconvex programs and show that the composite gradient descent algorithm is guaranteed to converge at a geometric rate to a neighborhood of the global minimizers: the size of the neighborhood is bounded by the statistical error in the $\ell_2$ norm. Our analysis reveals interesting connections between computational and statistical efficiency and the concentration of measure phenomenon in random matrix theory. We provide simulation evidence illuminating the theoretical predictions.

High dimensional errors-in-variables models with dependent measurements

Suppose that we observe $y \in \mathbb{R}^f$ and $X \in \mathbb{R}^{f \times m}$ in the following errors-in-variables model: \begin{eqnarray*} y & = & X_0 \beta^* + \epsilon \\ X & = & X_0 + W \end{eqnarray*} where $X_0$ is a $f \times m$ design matrix with independent subgaussian row vectors, $\epsilon \in \mathbb{R}^f$ is a noise vector and $W$ is a mean zero $f \times m$ random noise matrix with independent subgaussian column vectors, independent of $X_0$ and $\epsilon$. This model is significantly different from those analyzed in the literature in the sense that we allow the measurement error for each covariate to be a dependent vector across its $f$ observations. Such error structures appear in the science literature when modeling the trial-to-trial fluctuations in response strength shared across a set of neurons. Under sparsity and restrictive eigenvalue type of conditions, we show that one is able to recover a sparse vector $\beta^* \in \mathbb{R}^m$ from the model given a single observation matrix $X$ and the response vector $y$. We establish consistency in estimating $\beta^*$ and obtain the rates of convergence in the $\ell_q$ norm, where $q = 1, 2$ for the Lasso-type estimator, and for $q \in [1, 2]$ for a Dantzig-type conic programming estimator. We show error bounds which approach that of the regular Lasso and the Dantzig selector in case the errors in $W$ are tending to 0.

Spectral Norm of Random Kernel Matrices with Applications to Privacy

Kernel methods are an extremely popular set of techniques used for many important machine learning and data analysis applications. In addition to having good practical performances, these methods are supported by a well-developed theory. Kernel methods use an implicit mapping of the input data into a high dimensional feature space defined by a kernel function, i.e., a function returning the inner product between the images of two data points in the feature space. Central to any kernel method is the kernel matrix, which is built by evaluating the kernel function on a given sample dataset. In this paper, we initiate the study of non-asymptotic spectral theory of random kernel matrices. These are n x n random matrices whose (i,j)th entry is obtained by evaluating the kernel function on $x_i$ and $x_j$, where $x_1,...,x_n$ are a set of n independent random high-dimensional vectors. Our main contribution is to obtain tight upper bounds on the spectral norm (largest eigenvalue) of random kernel matrices constructed by commonly used kernel functions based on polynomials and Gaussian radial basis. As an application of these results, we provide lower bounds on the distortion needed for releasing the coefficients of kernel ridge regression under attribute privacy, a general privacy notion which captures a large class of privacy definitions. Kernel ridge regression is standard method for performing non-parametric regression that regularly outperforms traditional regression approaches in various domains. Our privacy distortion lower bounds are the first for any kernel technique, and our analysis assumes realistic scenarios for the input, unlike all previous lower bounds for other release problems which only hold under very restrictive input settings.

The Power of Linear Reconstruction Attacks

We consider the power of linear reconstruction attacks in statistical data privacy, showing that they can be applied to a much wider range of settings than previously understood. Linear attacks have been studied before (Dinur and Nissim PODS'03, Dwork, McSherry and Talwar STOC'07, Kasiviswanathan, Rudelson, Smith and Ullman STOC'10, De TCC'12, Muthukrishnan and Nikolov STOC'12) but have so far been applied only in settings with releases that are obviously linear. Consider a database curator who manages a database of sensitive information but wants to release statistics about how a sensitive attribute (say, disease) in the database relates to some nonsensitive attributes (e.g., postal code, age, gender, etc). We show one can mount linear reconstruction attacks based on any release that gives: a) the fraction of records that satisfy a given non-degenerate boolean function. Such releases include contingency tables (previously studied by Kasiviswanathan et al., STOC'10) as well as more complex outputs like the error rate of classifiers such as decision trees; b) any one of a large class of M-estimators (that is, the output of empirical risk minimization algorithms), including the standard estimators for linear and logistic regression. We make two contributions: first, we show how these types of releases can be transformed into a linear format, making them amenable to existing polynomial-time reconstruction algorithms. This is already perhaps surprising, since many of the above releases (like M-estimators) are obtained by solving highly nonlinear formulations. Second, we show how to analyze the resulting attacks under various distributional assumptions on the data. Specifically, we consider a setting in which the same statistic (either a) or b) above) is released about how the sensitive attribute relates to all subsets of size k (out of a total of d) nonsensitive boolean attributes.