Debiasing and a local analysis for population clustering using semidefinite programming

In this paper, we consider the problem of partitioning a small data sample of size $n$ drawn from a mixture of $2$ sub-gaussian distributions. In particular, we analyze computational efficient algorithms proposed by the same author, to partition data into two groups approximately according to their population of origin given a small sample. This work is motivated by the application of clustering individuals according to their population of origin using $p$ markers, when the divergence between any two of the populations is small. We build upon the semidefinite relaxation of an integer quadratic program that is formulated essentially as finding the maximum cut on a graph, where edge weights in the cut represent dissimilarity scores between two nodes based on their $p$ features. Here we use $\Delta^2 :=p \gamma$ to denote the $\ell_2^2$ distance between two centers (mean vectors), namely, $\mu^{(1)}$, $\mu^{(2)}$ $\in$ $\mathbb{R}^p$. The goal is to allow a full range of tradeoffs between $n, p, \gamma$ in the sense that partial recovery (success rate $< 100\%$) is feasible once the signal to noise ratio $s^2 := \min\{np \gamma^2, \Delta^2\}$ is lower bounded by a constant. Importantly, we prove that the misclassification error decays exponentially with respect to the SNR $s^2$. This result was introduced earlier without a full proof. We therefore present the full proof in the present work. Finally, for balanced partitions, we consider a variant of the SDP1, and show that the new estimator has a superb debiasing property. This is novel to the best of our knowledge.

Semidefinite programming on population clustering: a global analysis

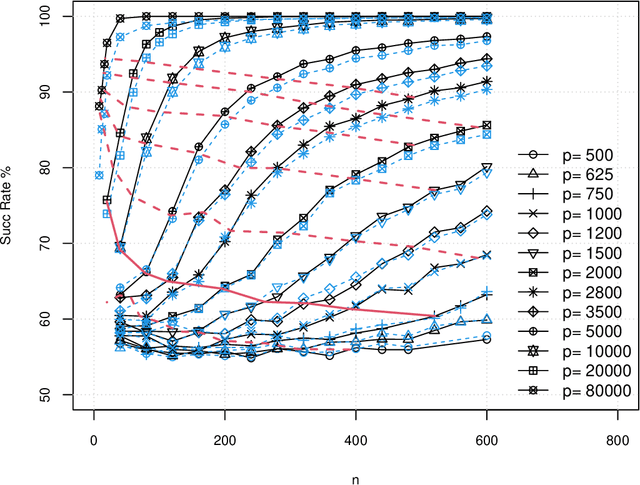
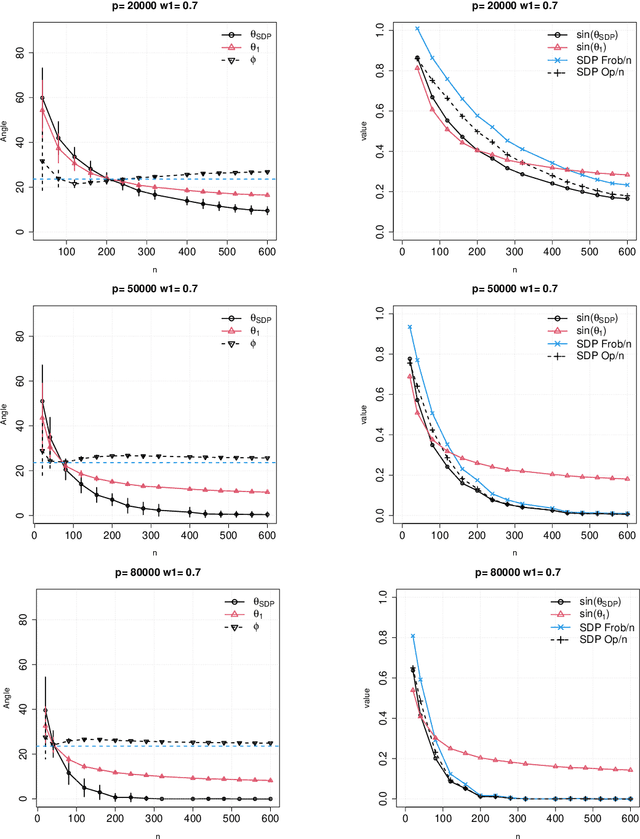
In this paper, we consider the problem of partitioning a small data sample of size $n$ drawn from a mixture of $2$ sub-gaussian distributions. Our work is motivated by the application of clustering individuals according to their population of origin using markers, when the divergence between the two populations is small. We are interested in the case that individual features are of low average quality $\gamma$, and we want to use as few of them as possible to correctly partition the sample. We consider semidefinite relaxation of an integer quadratic program which is formulated essentially as finding the maximum cut on a graph where edge weights in the cut represent dissimilarity scores between two nodes based on their features. A small simulation result in Blum, Coja-Oghlan, Frieze and Zhou (2007, 2009) shows that even when the sample size $n$ is small, by increasing $p$ so that $np= \Omega(1/\gamma^2)$, one can classify a mixture of two product populations using the spectral method therein with success rate reaching an ``oracle'' curve. There the ``oracle'' was computed assuming that distributions were known, where success rate means the ratio between correctly classified individuals and the sample size $n$. In this work, we show the theoretical underpinning of this observed concentration of measure phenomenon in high dimensions, simultaneously for the semidefinite optimization goal and the spectral method, where the input is based on the gram matrix computed from centered data. We allow a full range of tradeoffs between the sample size and the number of features such that the product of these two is lower bounded by $1/{\gamma^2}$ so long as the number of features $p$ is lower bounded by $1/\gamma$.

Precision Matrix Estimation with Noisy and Missing Data

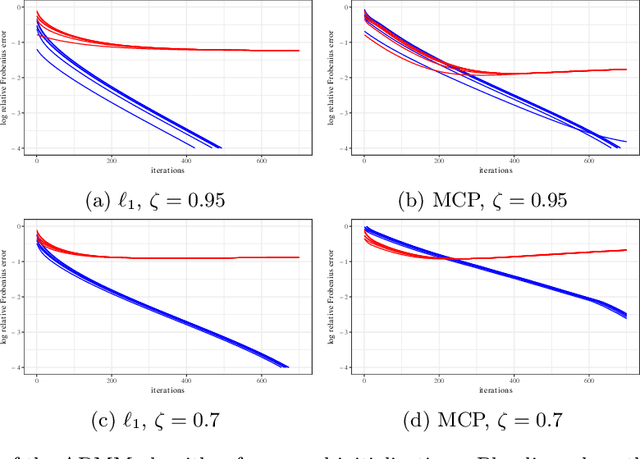
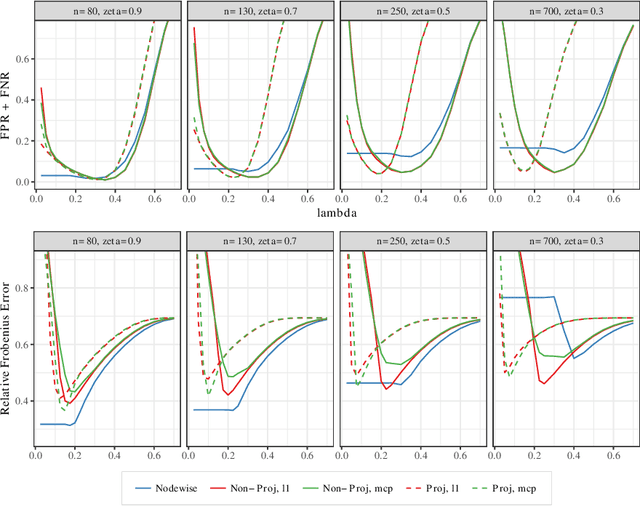
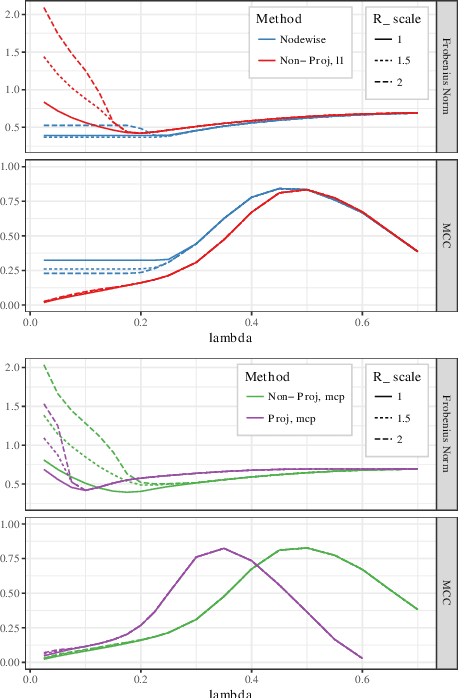
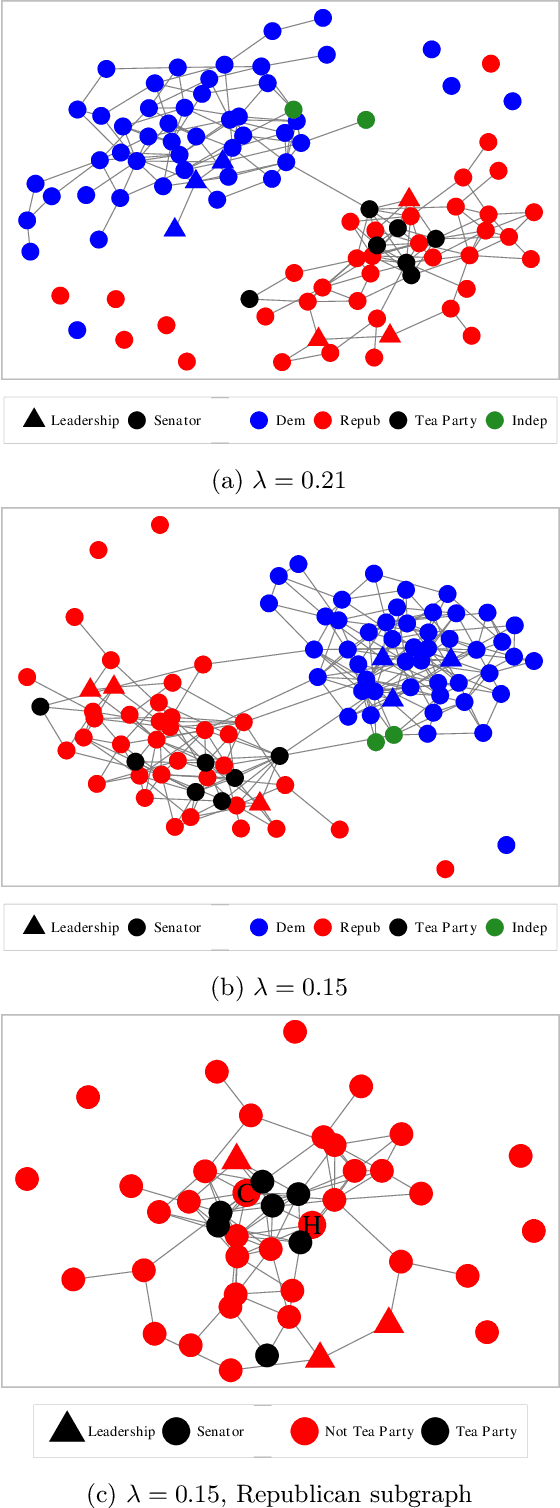
Estimating conditional dependence graphs and precision matrices are some of the most common problems in modern statistics and machine learning. When data are fully observed, penalized maximum likelihood-type estimators have become standard tools for estimating graphical models under sparsity conditions. Extensions of these methods to more complex settings where data are contaminated with additive or multiplicative noise have been developed in recent years. In these settings, however, the relative performance of different methods is not well understood and algorithmic gaps still exist. In particular, in high-dimensional settings these methods require using non-positive semidefinite matrices as inputs, presenting novel optimization challenges. We develop an alternating direction method of multipliers (ADMM) algorithm for these problems, providing a feasible algorithm to estimate precision matrices with indefinite input and potentially nonconvex penalties. We compare this method with existing alternative solutions and empirically characterize the tradeoffs between them. Finally, we use this method to explore the networks among US senators estimated from voting records data.

Joint mean and covariance estimation with unreplicated matrix-variate data

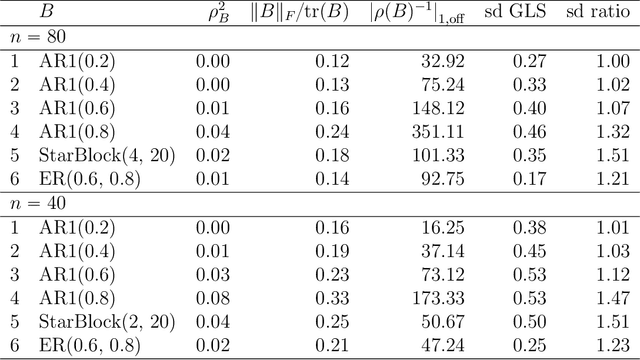
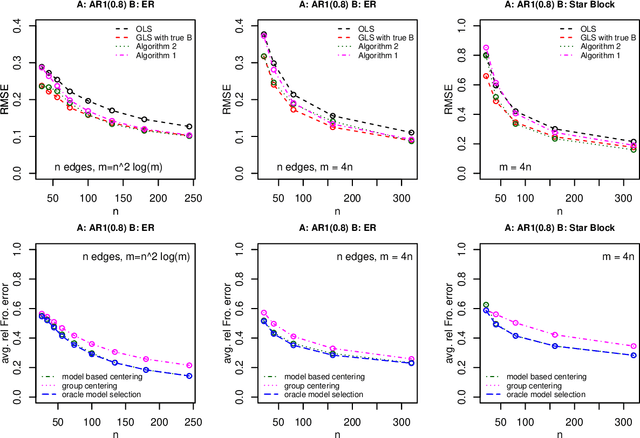
It has been proposed that complex populations, such as those that arise in genomics studies, may exhibit dependencies among observations as well as among variables. This gives rise to the challenging problem of analyzing unreplicated high-dimensional data with unknown mean and dependence structures. Matrix-variate approaches that impose various forms of (inverse) covariance sparsity allow flexible dependence structures to be estimated, but cannot directly be applied when the mean and covariance matrices are estimated jointly. We present a practical method utilizing generalized least squares and penalized (inverse) covariance estimation to address this challenge. We establish consistency and obtain rates of convergence for estimating the mean parameters and covariance matrices. The advantages of our approaches are: (i) dependence graphs and covariance structures can be estimated in the presence of unknown mean structure, (ii) the mean structure becomes more efficiently estimated when accounting for the dependence structure among observations; and (iii) inferences about the mean parameters become correctly calibrated. We use simulation studies and analysis of genomic data from a twin study of ulcerative colitis to illustrate the statistical convergence and the performance of our methods in practical settings. Several lines of evidence show that the test statistics for differential gene expression produced by our methods are correctly calibrated and improve power over conventional methods.

Errors-in-variables models with dependent measurements

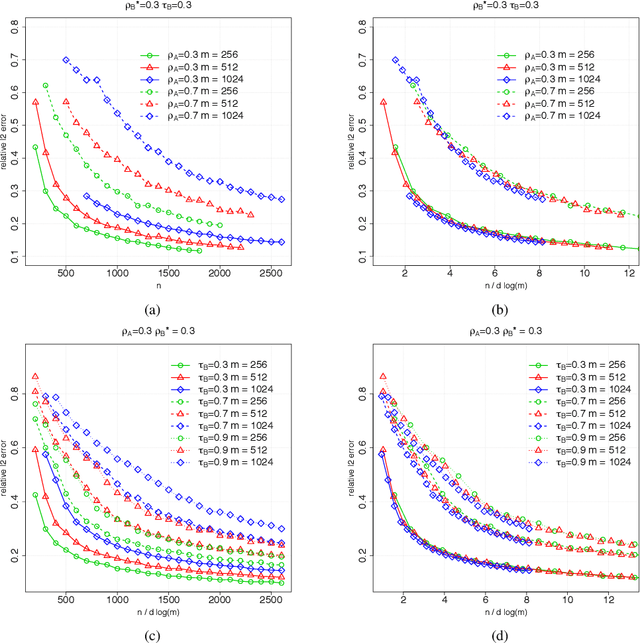
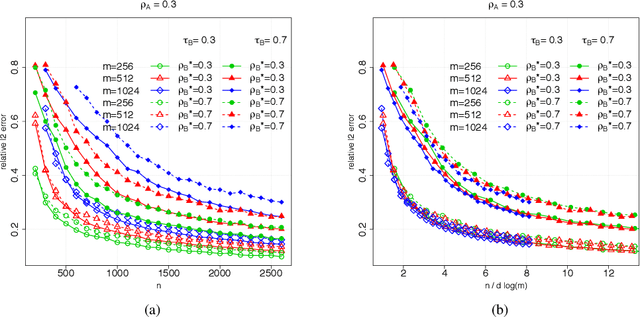
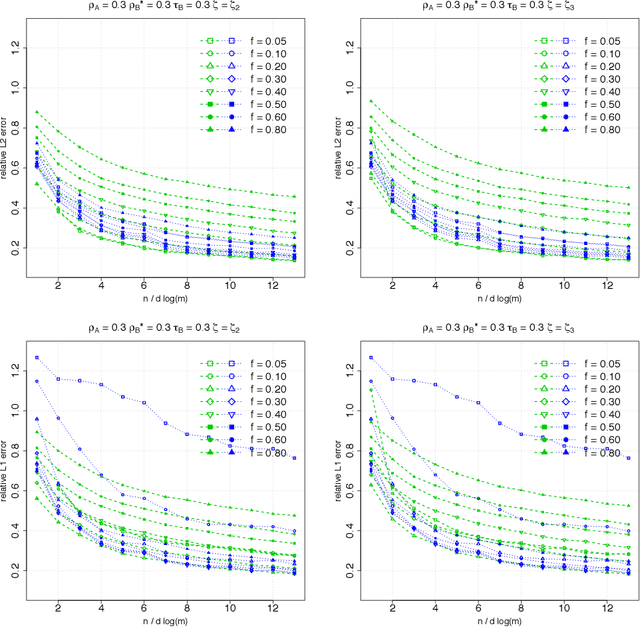
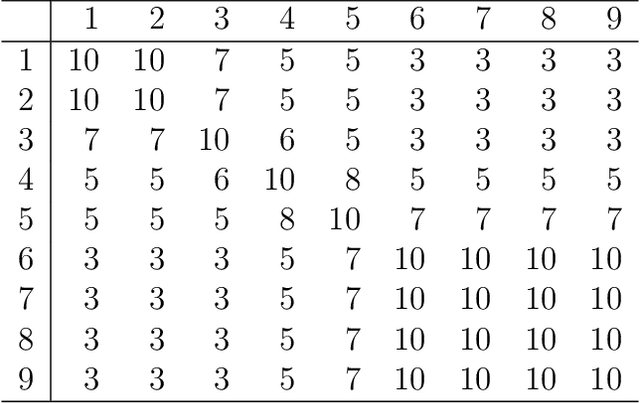
Suppose that we observe $y \in \mathbb{R}^n$ and $X \in \mathbb{R}^{n \times m}$ in the following errors-in-variables model: \begin{eqnarray*} y & = & X_0 \beta^* +\epsilon \\ X & = & X_0 + W, \end{eqnarray*} where $X_0$ is an $n \times m$ design matrix with independent subgaussian row vectors, $\epsilon \in \mathbb{R}^n$ is a noise vector and $W$ is a mean zero $n \times m$ random noise matrix with independent subgaussian column vectors, independent of $X_0$ and $\epsilon$. This model is significantly different from those analyzed in the literature in the sense that we allow the measurement error for each covariate to be a dependent vector across its $n$ observations. Such error structures appear in the science literature when modeling the trial-to-trial fluctuations in response strength shared across a set of neurons. Under sparsity and restrictive eigenvalue type of conditions, we show that one is able to recover a sparse vector $\beta^* \in \mathbb{R}^m$ from the model given a single observation matrix $X$ and the response vector $y$. We establish consistency in estimating $\beta^*$ and obtain the rates of convergence in the $\ell_q$ norm, where $q = 1, 2$. We show error bounds which approach that of the regular Lasso and the Dantzig selector in case the errors in $W$ are tending to 0. We analyze the convergence rates of the gradient descent methods for solving the nonconvex programs and show that the composite gradient descent algorithm is guaranteed to converge at a geometric rate to a neighborhood of the global minimizers: the size of the neighborhood is bounded by the statistical error in the $\ell_2$ norm. Our analysis reveals interesting connections between computational and statistical efficiency and the concentration of measure phenomenon in random matrix theory. We provide simulation evidence illuminating the theoretical predictions.

High dimensional errors-in-variables models with dependent measurements

Suppose that we observe $y \in \mathbb{R}^f$ and $X \in \mathbb{R}^{f \times m}$ in the following errors-in-variables model: \begin{eqnarray*} y & = & X_0 \beta^* + \epsilon \\ X & = & X_0 + W \end{eqnarray*} where $X_0$ is a $f \times m$ design matrix with independent subgaussian row vectors, $\epsilon \in \mathbb{R}^f$ is a noise vector and $W$ is a mean zero $f \times m$ random noise matrix with independent subgaussian column vectors, independent of $X_0$ and $\epsilon$. This model is significantly different from those analyzed in the literature in the sense that we allow the measurement error for each covariate to be a dependent vector across its $f$ observations. Such error structures appear in the science literature when modeling the trial-to-trial fluctuations in response strength shared across a set of neurons. Under sparsity and restrictive eigenvalue type of conditions, we show that one is able to recover a sparse vector $\beta^* \in \mathbb{R}^m$ from the model given a single observation matrix $X$ and the response vector $y$. We establish consistency in estimating $\beta^*$ and obtain the rates of convergence in the $\ell_q$ norm, where $q = 1, 2$ for the Lasso-type estimator, and for $q \in [1, 2]$ for a Dantzig-type conic programming estimator. We show error bounds which approach that of the regular Lasso and the Dantzig selector in case the errors in $W$ are tending to 0.

Gemini: Graph estimation with matrix variate normal instances

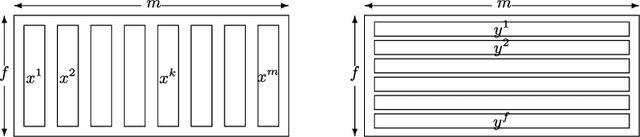
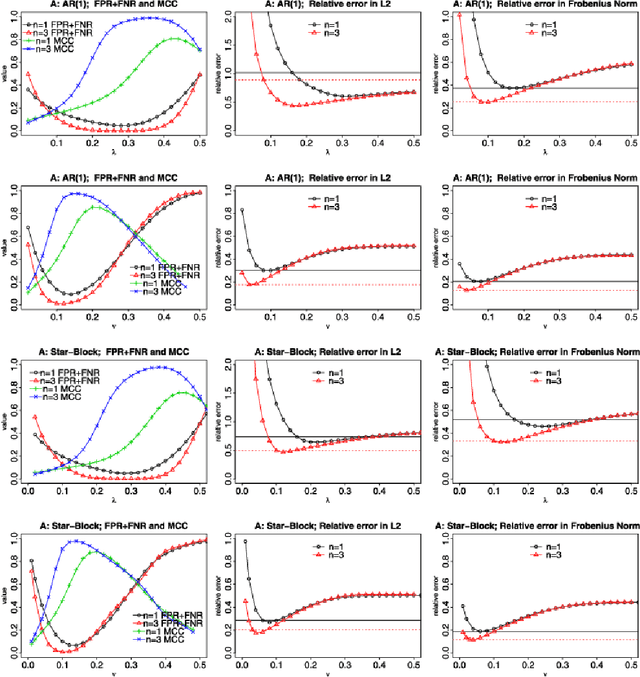
Undirected graphs can be used to describe matrix variate distributions. In this paper, we develop new methods for estimating the graphical structures and underlying parameters, namely, the row and column covariance and inverse covariance matrices from the matrix variate data. Under sparsity conditions, we show that one is able to recover the graphs and covariance matrices with a single random matrix from the matrix variate normal distribution. Our method extends, with suitable adaptation, to the general setting where replicates are available. We establish consistency and obtain the rates of convergence in the operator and the Frobenius norm. We show that having replicates will allow one to estimate more complicated graphical structures and achieve faster rates of convergence. We provide simulation evidence showing that we can recover graphical structures as well as estimating the precision matrices, as predicted by theory.

Convergence Properties of Kronecker Graphical Lasso Algorithms

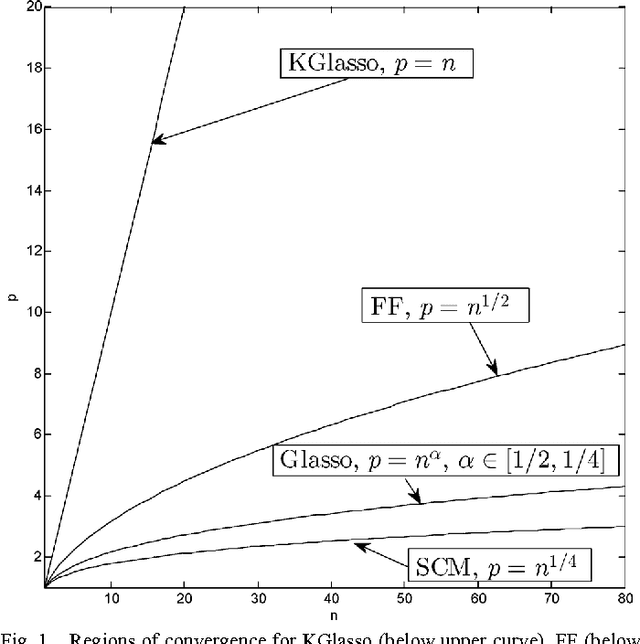
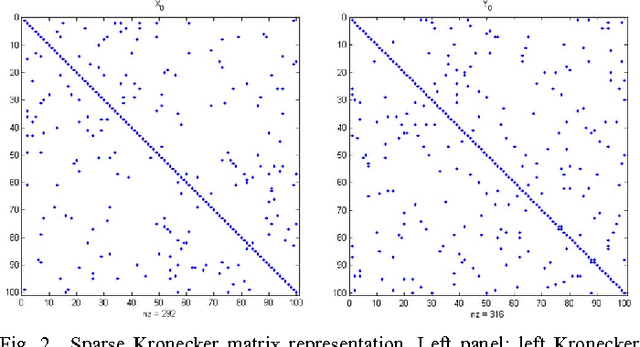
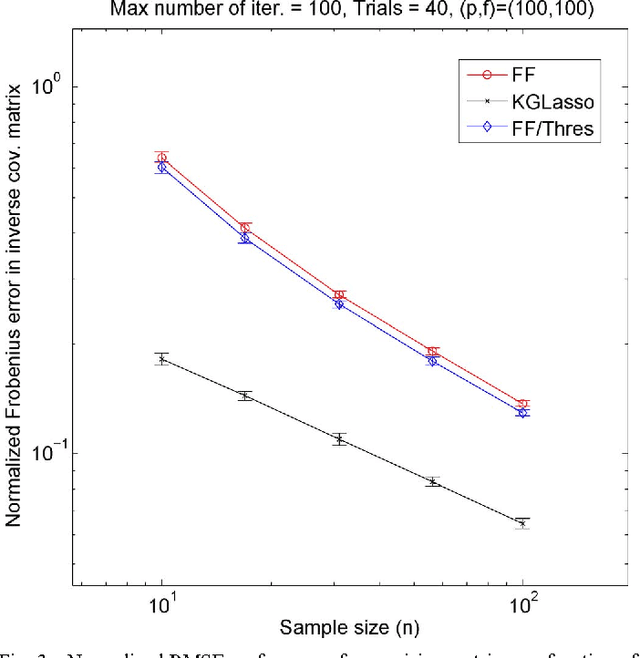
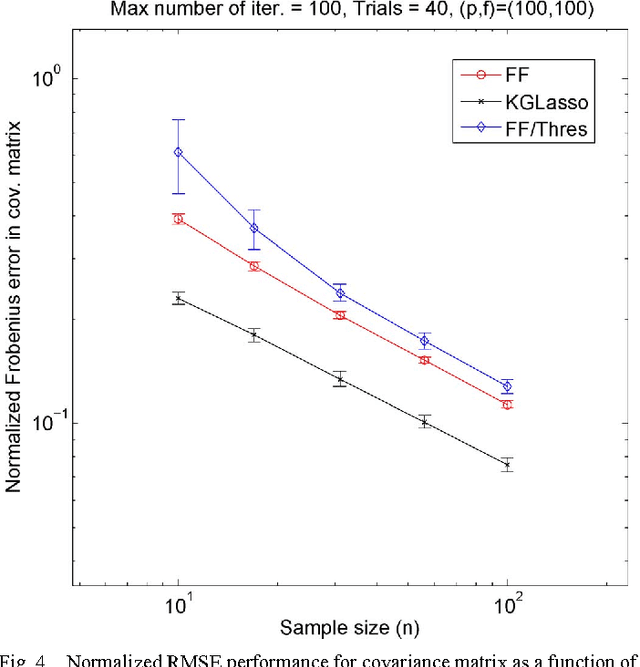
This paper studies iteration convergence of Kronecker graphical lasso (KGLasso) algorithms for estimating the covariance of an i.i.d. Gaussian random sample under a sparse Kronecker-product covariance model and MSE convergence rates. The KGlasso model, originally called the transposable regularized covariance model by Allen ["Transposable regularized covariance models with an application to missing data imputation," Ann. Appl. Statist., vol. 4, no. 2, pp. 764-790, 2010], implements a pair of $\ell_1$ penalties on each Kronecker factor to enforce sparsity in the covariance estimator. The KGlasso algorithm generalizes Glasso, introduced by Yuan and Lin ["Model selection and estimation in the Gaussian graphical model," Biometrika, vol. 94, pp. 19-35, 2007] and Banerjee ["Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data," J. Mach. Learn. Res., vol. 9, pp. 485-516, Mar. 2008], to estimate covariances having Kronecker product form. It also generalizes the unpenalized ML flip-flop (FF) algorithm of Dutilleul ["The MLE algorithm for the matrix normal distribution," J. Statist. Comput. Simul., vol. 64, pp. 105-123, 1999] and Werner ["On estimation of covariance matrices with Kronecker product structure," IEEE Trans. Signal Process., vol. 56, no. 2, pp. 478-491, Feb. 2008] to estimation of sparse Kronecker factors. We establish that the KGlasso iterates converge pointwise to a local maximum of the penalized likelihood function. We derive high dimensional rates of convergence to the true covariance as both the number of samples and the number of variables go to infinity. Our results establish that KGlasso has significantly faster asymptotic convergence than Glasso and FF. Simulations are presented that validate the results of our analysis.

High-dimensional covariance estimation based on Gaussian graphical models

Undirected graphs are often used to describe high dimensional distributions. Under sparsity conditions, the graph can be estimated using $\ell_1$-penalization methods. We propose and study the following method. We combine a multiple regression approach with ideas of thresholding and refitting: first we infer a sparse undirected graphical model structure via thresholding of each among many $\ell_1$-norm penalized regression functions; we then estimate the covariance matrix and its inverse using the maximum likelihood estimator. We show that under suitable conditions, this approach yields consistent estimation in terms of graphical structure and fast convergence rates with respect to the operator and Frobenius norm for the covariance matrix and its inverse. We also derive an explicit bound for the Kullback Leibler divergence.

Restricted Eigenvalue Conditions on Subgaussian Random Matrices

It is natural to ask: what kinds of matrices satisfy the Restricted Eigenvalue (RE) condition? In this paper, we associate the RE condition (Bickel-Ritov-Tsybakov 09) with the complexity of a subset of the sphere in $\R^p$, where $p$ is the dimensionality of the data, and show that a class of random matrices with independent rows, but not necessarily independent columns, satisfy the RE condition, when the sample size is above a certain lower bound. Here we explicitly introduce an additional covariance structure to the class of random matrices that we have known by now that satisfy the Restricted Isometry Property as defined in Candes and Tao 05 (and hence the RE condition), in order to compose a broader class of random matrices for which the RE condition holds. In this case, tools from geometric functional analysis in characterizing the intrinsic low-dimensional structures associated with the RE condition has been crucial in analyzing the sample complexity and understanding its statistical implications for high dimensional data.