Semidefinite programming on population clustering: a global analysis
Paper and Code
Jan 01, 2023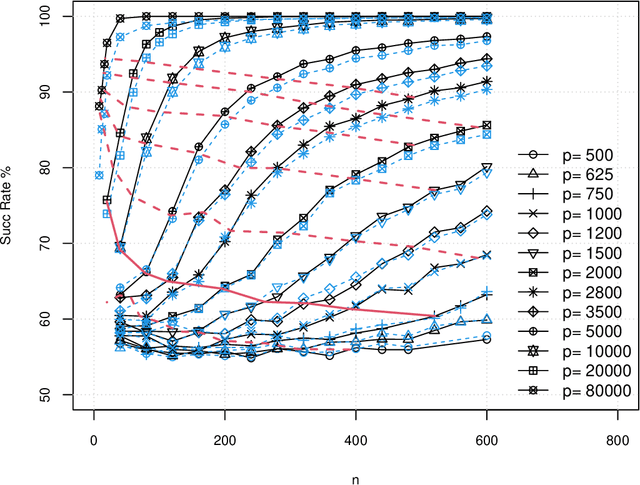
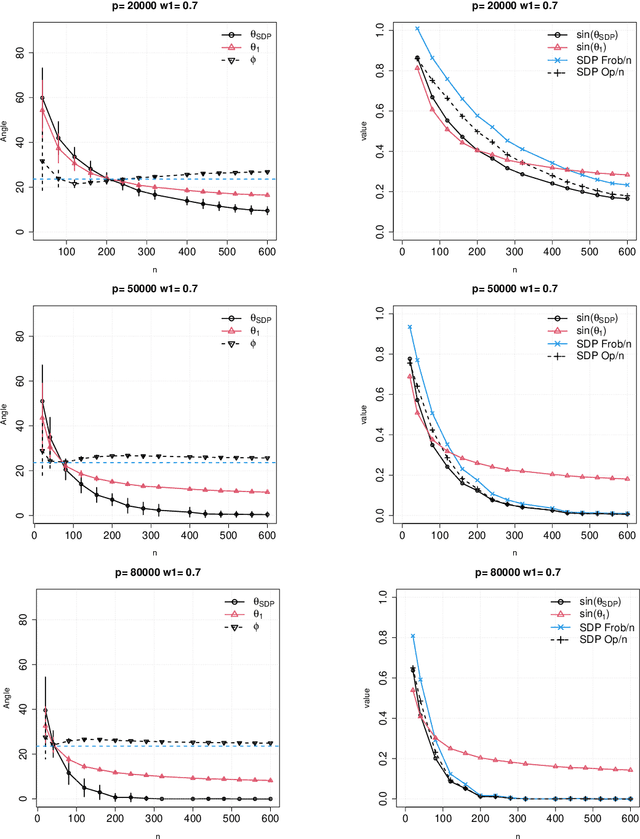
In this paper, we consider the problem of partitioning a small data sample of size $n$ drawn from a mixture of $2$ sub-gaussian distributions. Our work is motivated by the application of clustering individuals according to their population of origin using markers, when the divergence between the two populations is small. We are interested in the case that individual features are of low average quality $\gamma$, and we want to use as few of them as possible to correctly partition the sample. We consider semidefinite relaxation of an integer quadratic program which is formulated essentially as finding the maximum cut on a graph where edge weights in the cut represent dissimilarity scores between two nodes based on their features. A small simulation result in Blum, Coja-Oghlan, Frieze and Zhou (2007, 2009) shows that even when the sample size $n$ is small, by increasing $p$ so that $np= \Omega(1/\gamma^2)$, one can classify a mixture of two product populations using the spectral method therein with success rate reaching an ``oracle'' curve. There the ``oracle'' was computed assuming that distributions were known, where success rate means the ratio between correctly classified individuals and the sample size $n$. In this work, we show the theoretical underpinning of this observed concentration of measure phenomenon in high dimensions, simultaneously for the semidefinite optimization goal and the spectral method, where the input is based on the gram matrix computed from centered data. We allow a full range of tradeoffs between the sample size and the number of features such that the product of these two is lower bounded by $1/{\gamma^2}$ so long as the number of features $p$ is lower bounded by $1/\gamma$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge