Convergence Properties of Kronecker Graphical Lasso Algorithms
Paper and Code
Nov 01, 2013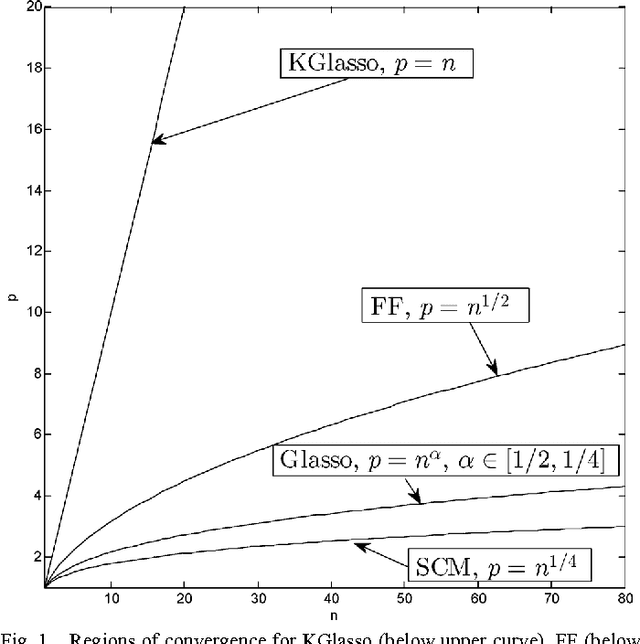
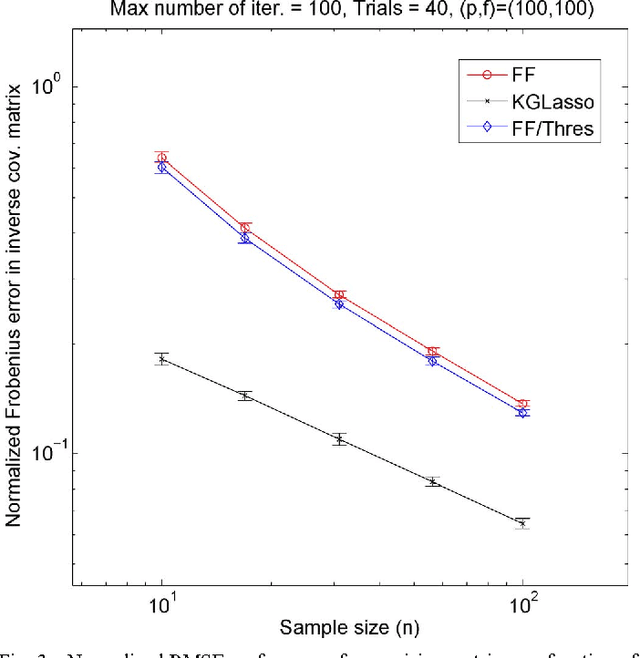
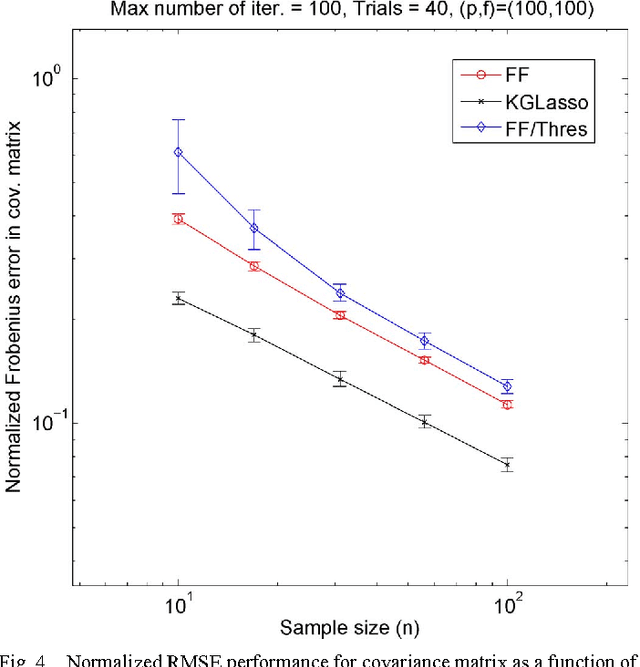
This paper studies iteration convergence of Kronecker graphical lasso (KGLasso) algorithms for estimating the covariance of an i.i.d. Gaussian random sample under a sparse Kronecker-product covariance model and MSE convergence rates. The KGlasso model, originally called the transposable regularized covariance model by Allen ["Transposable regularized covariance models with an application to missing data imputation," Ann. Appl. Statist., vol. 4, no. 2, pp. 764-790, 2010], implements a pair of $\ell_1$ penalties on each Kronecker factor to enforce sparsity in the covariance estimator. The KGlasso algorithm generalizes Glasso, introduced by Yuan and Lin ["Model selection and estimation in the Gaussian graphical model," Biometrika, vol. 94, pp. 19-35, 2007] and Banerjee ["Model selection through sparse maximum likelihood estimation for multivariate Gaussian or binary data," J. Mach. Learn. Res., vol. 9, pp. 485-516, Mar. 2008], to estimate covariances having Kronecker product form. It also generalizes the unpenalized ML flip-flop (FF) algorithm of Dutilleul ["The MLE algorithm for the matrix normal distribution," J. Statist. Comput. Simul., vol. 64, pp. 105-123, 1999] and Werner ["On estimation of covariance matrices with Kronecker product structure," IEEE Trans. Signal Process., vol. 56, no. 2, pp. 478-491, Feb. 2008] to estimation of sparse Kronecker factors. We establish that the KGlasso iterates converge pointwise to a local maximum of the penalized likelihood function. We derive high dimensional rates of convergence to the true covariance as both the number of samples and the number of variables go to infinity. Our results establish that KGlasso has significantly faster asymptotic convergence than Glasso and FF. Simulations are presented that validate the results of our analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge