Precision Matrix Estimation with Noisy and Missing Data
Paper and Code
Apr 07, 2019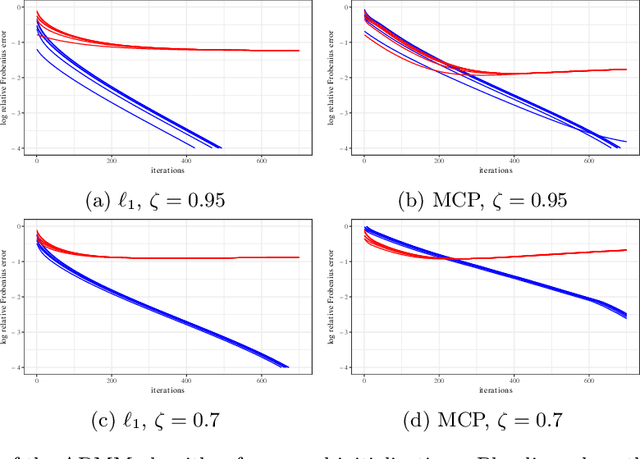
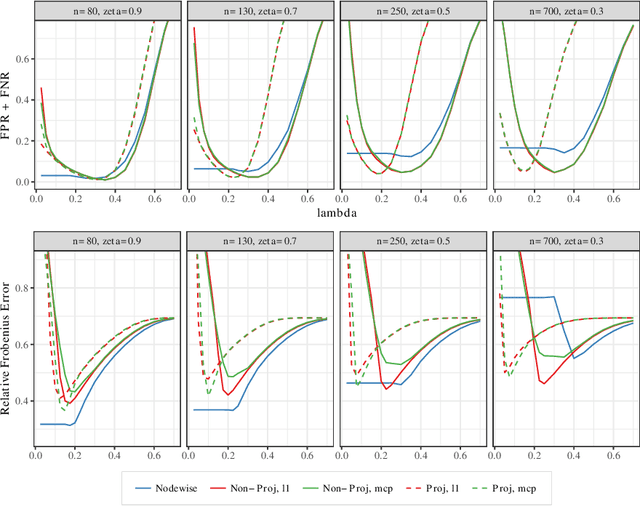
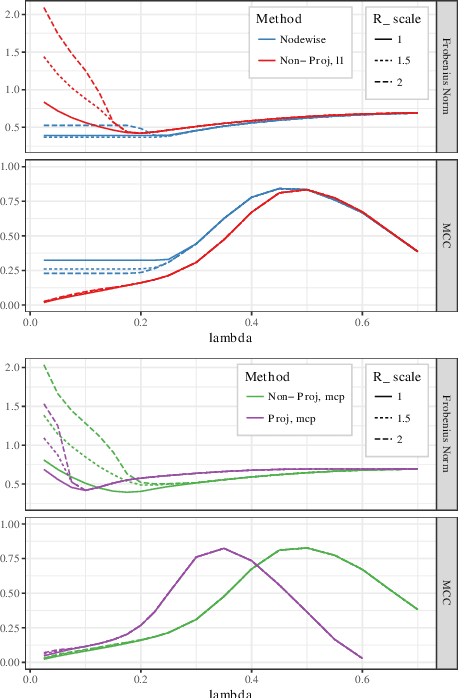
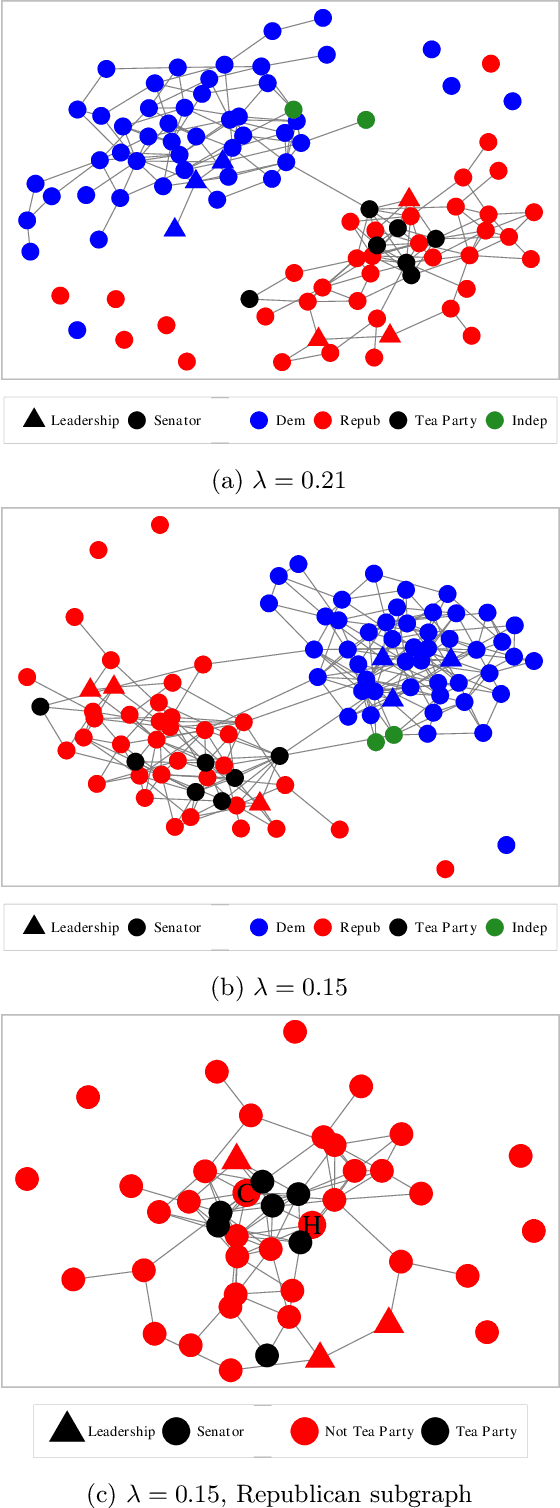
Estimating conditional dependence graphs and precision matrices are some of the most common problems in modern statistics and machine learning. When data are fully observed, penalized maximum likelihood-type estimators have become standard tools for estimating graphical models under sparsity conditions. Extensions of these methods to more complex settings where data are contaminated with additive or multiplicative noise have been developed in recent years. In these settings, however, the relative performance of different methods is not well understood and algorithmic gaps still exist. In particular, in high-dimensional settings these methods require using non-positive semidefinite matrices as inputs, presenting novel optimization challenges. We develop an alternating direction method of multipliers (ADMM) algorithm for these problems, providing a feasible algorithm to estimate precision matrices with indefinite input and potentially nonconvex penalties. We compare this method with existing alternative solutions and empirically characterize the tradeoffs between them. Finally, we use this method to explore the networks among US senators estimated from voting records data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge